5.6. Методы измерений вероятностных характеристик случайных процессов

 

Вероятностные характеристики случайного процесса определяются либо усреднением по совокупности ансамбля реализаций х_i(t):

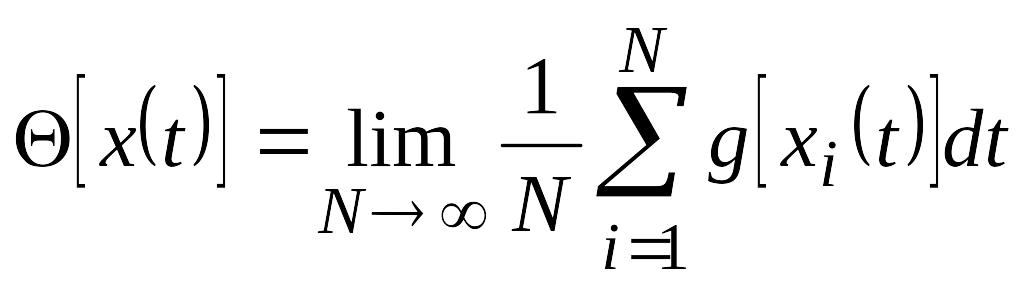, (5.36)

где g[x_i(t)] – некоторое преобразование, лежащее в основе определения вероятностной характеристики,

либо усреднением по времени с использование k-й реализации:

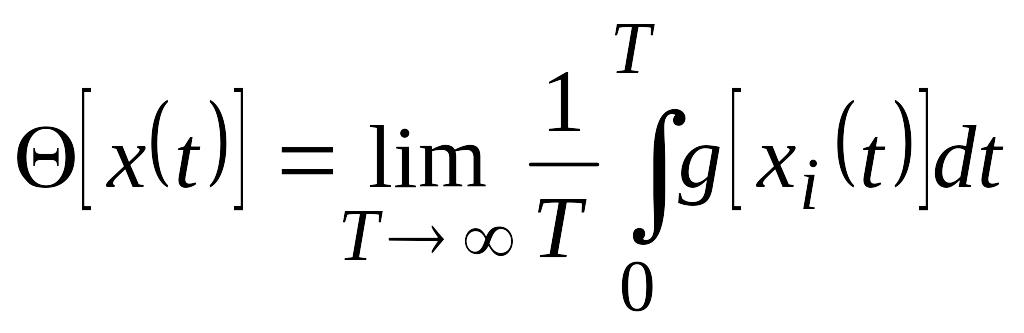. (5.37)

Как и другие измерения, измерение статистических характеристик производится с помощью специальных средств, реализующих алгоритм измерений, в том числе и меры, воспроизводящей известную величину.

Используют [15] три алгоритма измерений:

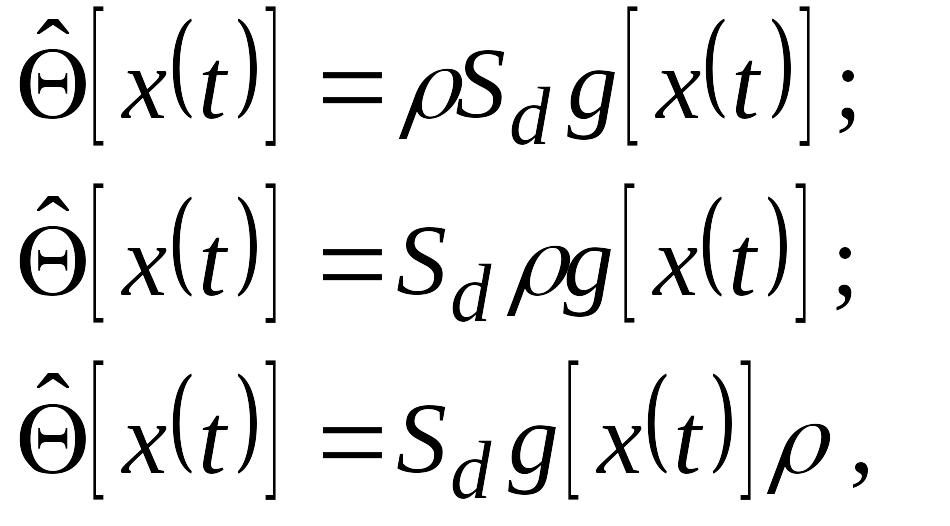(5.38)

где S_d – оператор усреднения (если усреднение по совокупности d=N, если усреднение по времени, d=Т), r - оператор сравнения, – результат измерения (оценка) характеристики .

Как видно, алгоритмы (5.36) отличаются только позициями, занимаемыми в выражении соответствующими операторами. Операция сравнения с мерой может быть: первой в цепи преобразований, второй – после реализации оператора g; и последней, что и отражено в структурных схемах (рис. 5.15).

 

Рис. 5.15. Структура измерений вероятностных характеристик случайных

процессов: а - сравнение с образцовой мерой является первой операцией;

б - выполняется до усреднения; в - является заключительной операцией

 

Обозначения структурных элементов на схемах соответствуют обозначениям тех операторов, которые ими реализуются. В качестве устройства усреднения S_d может быть использован сумматор или интегратор.

На рис. 5.15, а показана реализация следующей процедуры: на первом этапе с помощью блока r формируется массив числовых эквивалентов мгновенных значений реализаций случайного процесса, после чего преобразование g и усреднение S_d проходят в цифровой форме. Эти процессы могут быть реализованы последовательным соединением аналого-цифрового преобразователя и вычислительного устройства (например, микропроцессорного). На выходе АЦП формируется массив мгновенных значений, а процессор по определенной программе обеспечивает реализацию операторов g и S_d.

Процедура, осуществляемая структурой б (см.рис.5.15), начинается с преобразования совокупности реализаций {x_i(t)} в совокупность преобразованных реализаций {g[x_i(t)]}; затем с помощью компаратора r выполняется сравнение с известной величиной g₀. На выходе компаратора формируется числовой массив {g^*[x_i(t_i)]}, который поступает в вычислительное устройство, осуществляющее операцию усреднения S_d и выдающее результат в цифровой форме.

Структура, показанная на схеме в (см.рис. 5.15) реализует процедуру измерений, которая на первом этапе проходит так же, как в предыдущем случае, но затем совокупность {g[x_i(t)]} поступает на усреднение S_d, после которого величина S_d[{g[x_i(t)]}] поступает на компаратор r, осуществляющий сравнение с известной величиной q₀ . На выходе компаратора имеем .

Рассмотрим алгоритмы измерений основных статистических характеристик [15].

Измерение математического ожидания. Чаще всего производится усреднением по времени.

Алгоритм измерения:

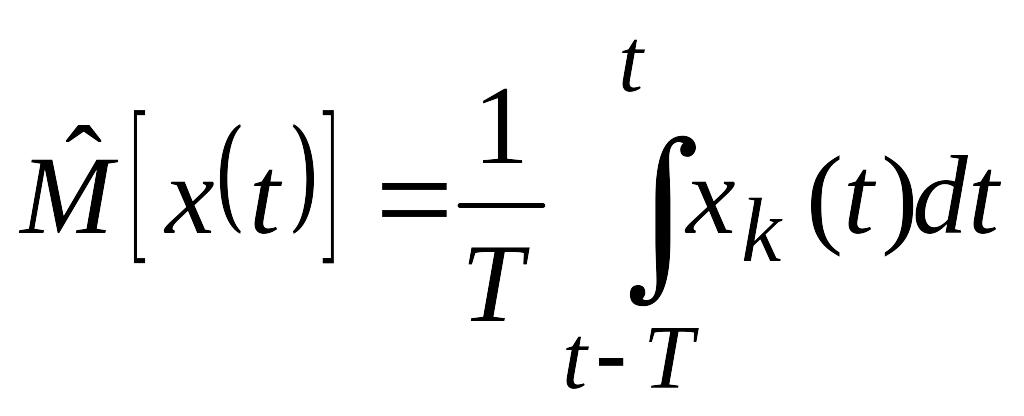. (5.39)

Структурная схема реализации данного алгоритма (рис. 5.16) в простейшем случае включает набор последовательно соединенных масштабного преобразователя МП, интегратора И, аналогового измерителя АИ.

Рис. 5.16. Структура измерений математического ожидания

 

Основным преобразователем в измерительной цепи является интегратор И, осуществляющий усреднение по времени. Возможны варианты схемы с выходом интегратора на цифровой измерительный прибор, самопишущий прибор и т.д.

Дисперсия случайного процесса характеризует математическое ожидание квадрата отклонения мгновенных значений реализаций от математического ожидания.

Алгоритм измерений, реализуемый структурой, представленной на рис.5.17:

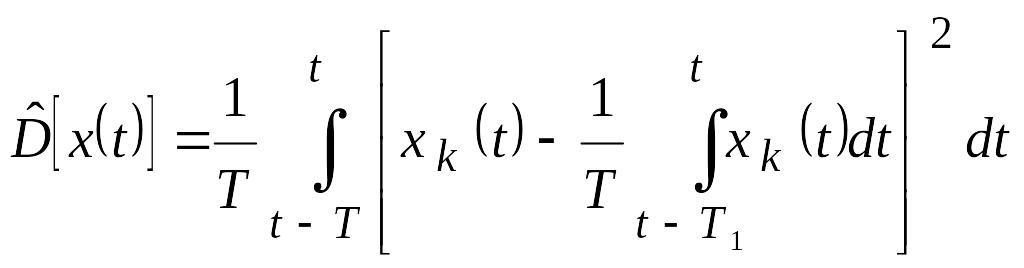. (5.40)

Одномерная интегральная функция распределения F(х), определяемая как вероятность того, что в произвольный момент времени мгновенное значение реализации не превысит заданного уровня, т.е. x_i(t_j)£x, определяется как предел выборочного среднего

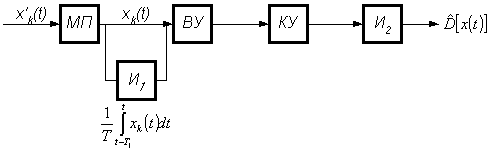, (5.41)

где

 

Рис. 5.17. Структура измерений дисперсии случайного процесса:

ВУ – вычитатель; КУ - квадратирующее устройство

 

Практически выражение (5.41) представляется как алгоритм измерения оценки в виде

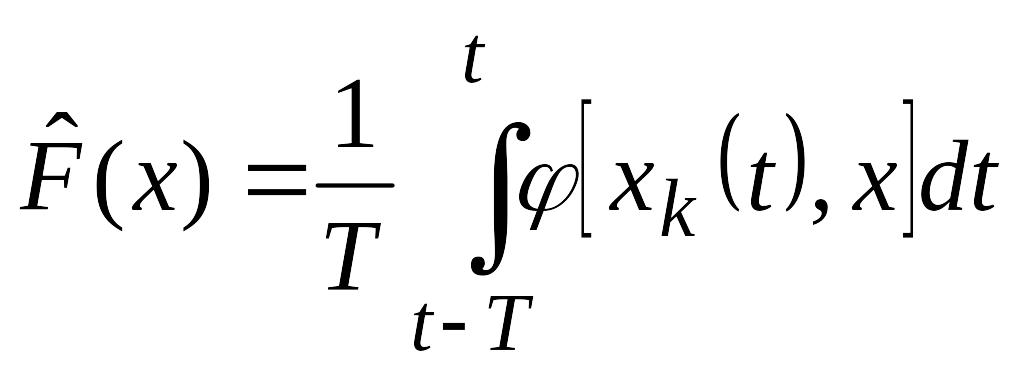. (5.42)

Обобщенная схема реализации алгоритма (5.42) показана на рис.5.18. Здесь: УС устройство сравнения, работающее в режиме вычитателя, формирующего сигнал x_k(t)-x; ФП – функциональный преобразователь, р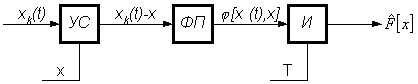 еализующий функцию j[ x_k(t),x], И – интегратор, Т- время наблюдения.

 

Рис. 5.18. Структурная схема измерения интегральной функции

распределения вероятности

 

Выражение для алгоритма измерения дифференциальной функции распределения вероятностей f(x) может быть получено, если учесть, что f(x) и F(x) связаны между собой известными соотношениями:

.

 

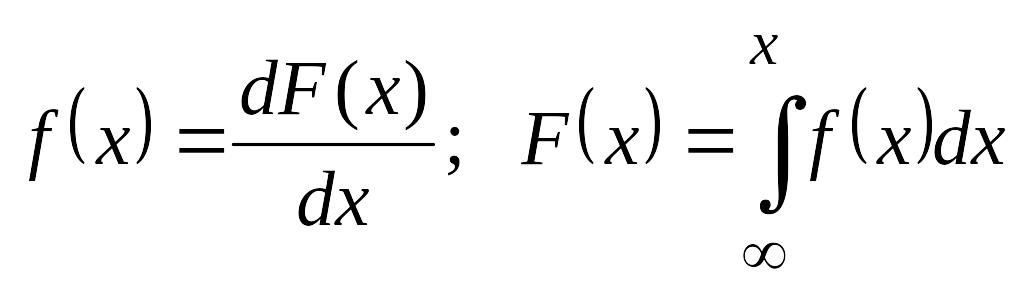Тогда справедливо выражение

, (5.43)

где

При соблюдении условий стационарности и эргодичности интегральная функция распределения может характеризоваться относительным временем пребывания значений реализации ниже заданного уровня х:

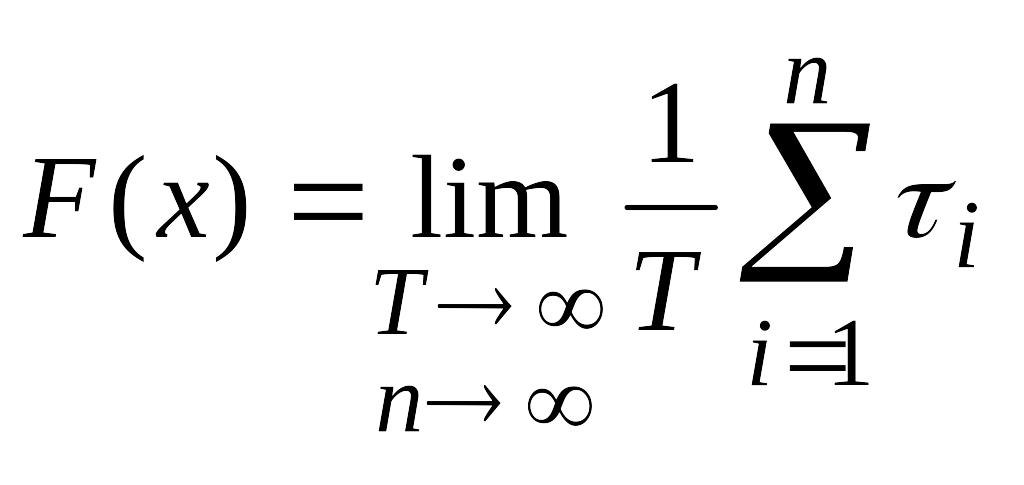, (5.44)

где i – интервал времени пребывания; n – число интервалов.

Соответственно выражение для дифференциальной функции можно представить в виде

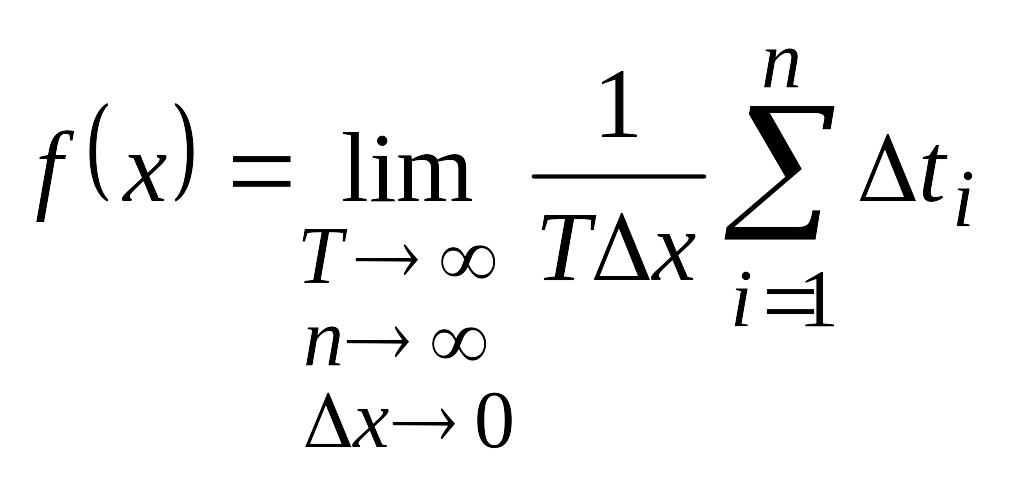, (5.45)

где Dх – ширина «дифференциального коридора», т.е. расстояние между соседними уровнями х_к и х_к+1; Dt_i – i -й интервал времени пребывания реализации между уровнями х_к и х_к+1.

На основании (5.44) и (5.45) алгоритмы измерений:

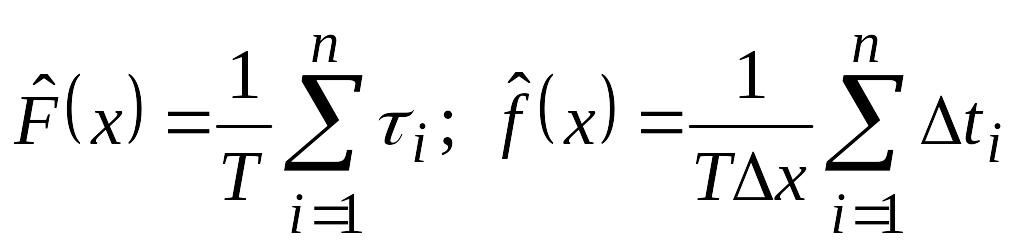. (5.46)

Применяются и другие алгоритмы, например, основанные на методе дискретных выборок.

Измерение корреляционной функции с усреднением по времени производятся по алгоритму

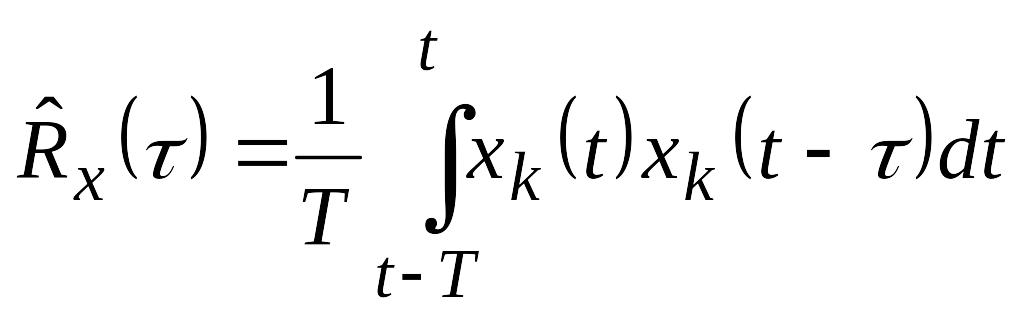. (5.47)

Структура измерительного устройства, реализующего данный алгоритм, представлена на рис. 5.19.

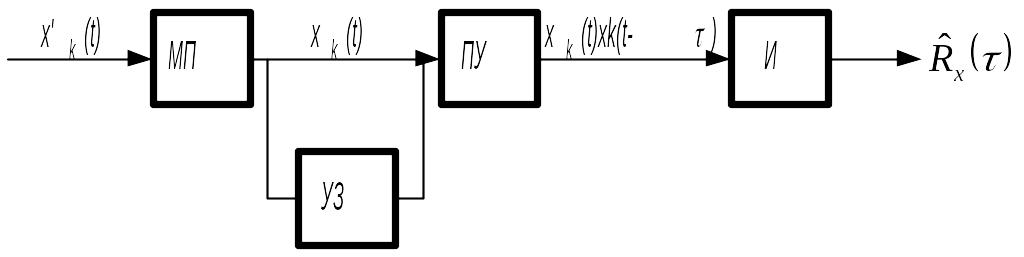
Рис. 5.19. Схема измерений корреляционной функции

 

С выхода масштабного преобразователя МП сигнал разветвляется, одновременно поступая на перемножающее устройство ПУ и на устройство временной задержки УЗ, с помощью которого получается сигнал x_k(t-t). Этот сигнал также поступает на ПУ, осуществляющее перемножение мгновенных значений, сдвинутых на интервал t. Результирующий сигнал поступает на интегратор И, с помощью которого осуществляется операция усреднения. На выходе интегратора получаем оценку корреляционной функции .

Измерение спектра мощности сигнала производится в соответствии с формулой

, (5.48)

где x_iT(w) - спектральная плотность сигнала на интервале усреднения Т, определяется согласно преобразованию Фурье по формуле

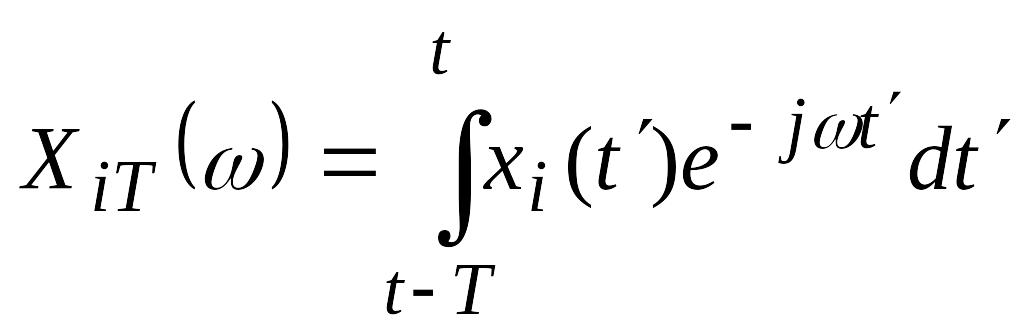. (5.49)

В соответствии с (5.48) алгоритм измерения

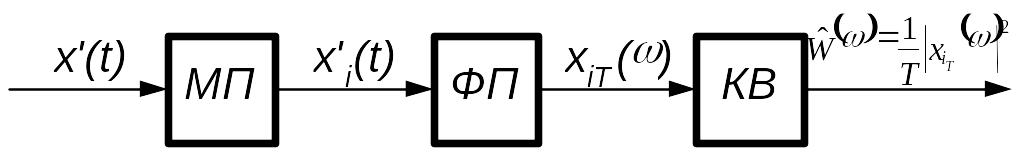. (5.50)

Схема реализации данного алгоритма показана на рис. 5.20.

 

Рис. 5.20. Схема измерения спектра мощности

 

Нормированный сигнал i -й реализации с масштабного преобразователя МП поступает на функциональный преобразователь ФП, выполняющий преобразование Фурье. Затем с помощью квадратирующего преобразователя КВ производится возведение в квадрат и нормирование с учетом интервала усреднения Т.