Добавил:

guap4736_vkclub152685050 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный минерально-сырьевой университет «Горный»

Предмет:

Добыча нефти и газа

Файл:

Нефтегазовая гидромеханика

.pdf

Скачиваний:

Добавлен:

31.08.2019

Размер:

19.68 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 5813 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

vk.com/club152685050 | vk.com/id446425943

F(z) = A In (reiθ) = A In r + iAθ.
Значит
=Alnr; =Aθ.	(7.48)
Приравнивая эти значения и		постоянным, найдем уравнения
эквипотенциальных линий и линий тока в следующем виде:
для эквипотенциальных линий – ν=const			(7.49)
для линии тока – θ = const.			(7.50)

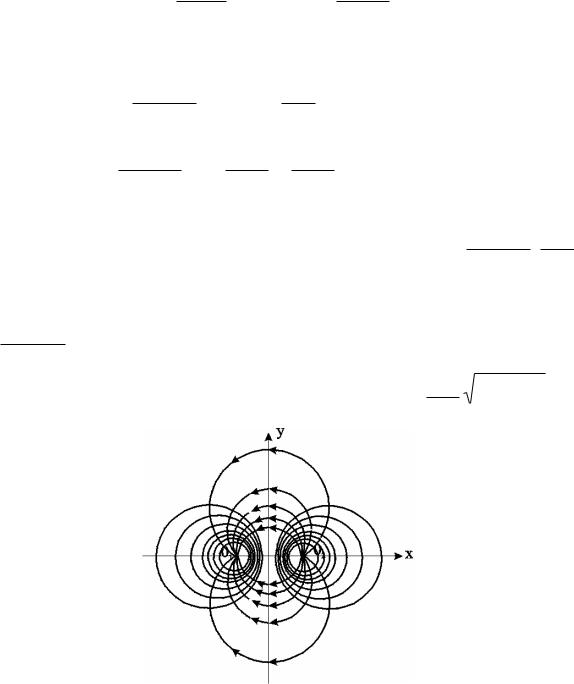
Очевидно, эквипотенциальные линии будут концентрическими окружностями с центром в начале координат (рис. 7.22). Линии тока – прямые, проходящие через начало координат.

В данном случае имеется плоскорадиальный (сходящийся или расходящийся) поток. Центр скважины (сток или источник) находится в начале координат.

Найдем массовую скорость фильтрации, для чего вычислим производную от функции F (7.46) по z:

	dF		A
	dz		z

Эта производная – комплексное

A	e	i
r
		.

переменное, модуль которого равен массовой

	u	dF
		dz
	скорости и представляет собой множитель перед е-iθ. Следовательно

(7.51)

то есть массовая скорость фильтрации обратно пропорциональна расстоянию

скважины. (Точка г = 0 является особой точкой плоскости; здесь u и функция F уже не будет аналитической). Для плоскорадиального потока имеем:

A
r	,
	,

от

(z)

u		G
u	2	hr
	2	hr
		,

где G = const – массовый дебит; Приравнивая правые части (7.51) и

h– мощность пласта.

(7.52), определим коэффициент А:

(7.52)

	A	G
	A	2 h
		2 h
		.

Подставив это значение А в формулу (7 .4 6 ), получим

(7.53)

F(z)	G	ln z
	2 h
		,	(7.54)

где положительный дебит G соответствует			случаю стока (эксплуатационной

скважине), а отрицательный - случаю источника (нагнетательной скважине).

Таким образом, функция (7.54) характеризует плоскорадиальное движение жидкости или газа в однородном горизонтальном пласте неограниченной протяженности. Скважина предполагается гидродинамически совершенной.

II. b) Пусть характеристическая функция имеет вид:

	F(z)	G
	F(z)	2 h
		2 h

ln(z а)

(7.55)

где а = а1 + ia2.

Это значит, что особая точка, в которой помещается точечный сток или точечный источник, сдвинута в направлении оси 0х на расстояние а1., а в направлении оси 0y на расстояние a2, и следовательно, центр поперечного сечения скважины находится не в начале координат, а в точке а = а1 + ia2.

110

vk.com/club152685050 | vk.com/id446425943

Если представить комплексное переменное z-а

получим				ln re
F(z)	G	ln(z а)	G		i	G	ln r
	2 h		2 h			2 h

где r – расстояние любой точки плоскости потока особой точки а = а1 + ia2, в которой помещается сток или вершиной в этой особой точке.

В соответствии с формулами (7.48) и (7.56)

в полярных координатах, то

G	i
2 h
	,	(7.56)

не до начала координат, а до источник; θ– полярный угол с

	G	ln r;	G	.
	2 h		2 h
					(7.57)

П р и м е ч а н и е . Потенциальная функция и					функция тока определяются с

точностью до произвольной постоянной. В формулах (7.57), выражающих и , опущены произвольные постоянные, но их надо учитывать при определении дебита.

III. Пусть в основной плоскости течения имеется несколько точечных стоков и источников (несколько эксплуатационных и нагнетательных скважин).

Потенциальную функцию течения, поддерживаемого всеми стоками и источниками , можно определить по методу суперпозиции, описанному в параграфе 7.1, как алгебраическую сумму потенциальных функций течений, поддерживаемых отдельными стоками и источниками, если бы каждый из них был единственным в пласте.

На основании первого равенства (7.57) запишем

n	n	G
j		j	ln r j
		2 h
j 1	j 1		,	(7.58)

где Gj – массовый дебит стока или источника за номером j; rj – расстояние любой точки плоскости потока до этого стока или источника; n – число стоков и источников.

Метод суперпозиции основан на известных свойствах уравнения Лапласа, которому подчиняется потенциал , а именно, сумма частных решений уравнения Лапласа есть решение этого уравнения.

В то же время существование потенциальной функции j означает существование наряду с ней функции тока j, соответствующей каждому стоку и источнику. Функция j удовлетворяет уравнению Лапласа; следовательно, по отношению к функции тока можно применять метод суперпозиции. Функция тока для течения, поддерживаемого всеми стоками и источниками, определится аналогично потенциалу сложного потока:

	n

	j 1

Характеристическая функция 7.59), определится уравнением:

	n	G
j		j	j
j		2 h	j
	j 1	2 h	.
	j 1

сложного потока,

(7.59)

согласно формулам (7.34), (7.58,

F(z) i

i j

G j

(ln r j i j )

j 1

j 1 2 h

j 1

где Fj (z) – характеристическая

функция,

соответствующая

за номером j, находящемуся в точке аj-:

Fj (z)

G j

i j

G j

ln z a j

ln r j e

2 h

F j (z).

(7.60)

стоку или источнику

(7.61)

111

vk.com/club152685050 | vk.com/id446425943

7.4.4. Характеристическая функция течения при совместном действии источника и стока

Рис. 7.23. Схема расположения источника 01 и стока 02

В разделе 7.1.6. подробно исследовалось семейство изобар в случае потока от нагнетательной скважины к эксплуатационной. О линиях тока было замечено, что они образуют семейство окружностей, ортогональных изобарам. Уточним вопрос об особенностях семейства линий тока на основе метода теории функций комплексного переменного.

Сохраняя прежние обозначения и придерживаясь рис. 7.23, получим на основании формул (7.60) и (7.61) характеристическую функцию течения от нагнетательной скважины к эксплуатационной

F(z)

ln z a

ln z

2 h

(7.62)

z a

r e

2 h

z a

2 h

где r1 и r2– расстояния некоторой точки М до источника 01 и стока 02 , соответственно, θ1 и θ2 – соответствующие полярные углы; М – модуль массового дебита стока и источника.

Отделяя в (7.62) действительную часть от мнимой, получим

F(z) i	G	ln	r1	i	G	(	2	)

	2 h r2				2 h	1
								,	(7.63)

Отсюда:

G			r			G
		ln		1	;
2	h		r			2	h
				2

Из (7.64) следует, что уравнение семейства

(		2	).
1		2

изобар запишется в виде

(7.64)

	r1	С
	r2
		,

где С – постоянное.
Уравнение линий тока получается из второй формулы (7.64):
θ1-θ2=С*,			(7.65)

где С* – постоянное.

Рассмотрим уравнение (7.65). Выразим θ1 и θ2 через координаты точки М (х, у) в соответствии с рис. 7.23.

112

vk.com/club152685050 | vk.com/id446425943

	arctg	y	;		arctg	y
	arctg		;	2	arctg
1		x a		2		x a
		1				2	.
							.

Подставив значения θ1 и θ2 в уравнение (7.65) и учитывая, что а2-a1=2a, будем иметь после несложных алгебраических преобразований:

		a		a	2		2						a					2
		a		a
		1							y
x									y					* *
				2								C		* *
				2								C
	a	2	a			2		a		2				a		2				* *	2
	a		a																		2
				1
			2						* *		2				* *		2		C			1
			2					C	* *				C		* *

где С** - новая постоянная.

(7.66)

	a		a	2		a
		1		2	,
			2			C	* *
Из (7.66) видно, что центры окружностей имеют координаты			2			C		.
Из (7.66) видно, что центры окружностей имеют координаты								.

Так как абсцисса центров окружностей не зависит от С * * , то она одинакова для всех

окружностей и,					следовательно,	все окружности расположены на прямой
	a	a	2
x	1		2	a	a
		2		1	, То есть на	прямой, параллельной оси 0у, делящей расстояние
		2

R	a		C	**	2	1
				**

1	C	**
между стоком и источником пополам. Радиус окружностей		**				.

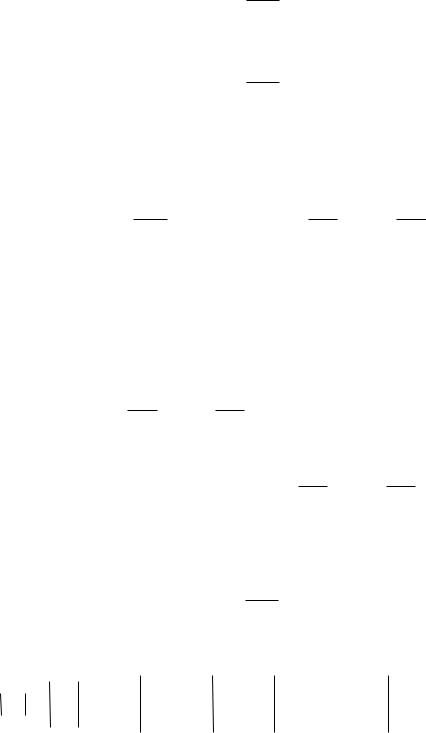
Рис. 7.24. Фильтрационное поле источника и стока

Отсюда абсциссы точек пересечения

x		a	2a a	;
1		1	2
x	2	a	a a a		,
	2	1		1

то есть линии тока проходят через сток и источник.

Таким образом, линии тока представляют собой окружности, проходящие через центры обеих скважин, и ортогональны окружностям - изобарам. Центры всех этих окружностей расположены на прямой (эквипотенциальной линии), делящей расстояние между скважинами пополам (рис. 7.24).

113

vk.com/club152685050 | vk.com/id446425943

7.4.5. Характеристическая функция течения для кольцевой батареи скважин

Характеристическую функцию для п стоков представим в виде:

	G		n
F(z)			Fj	(s)
	2
		b
			j 1	.	(7.67)

Согласно формуле (7.61), можно записать
	G		n
F(z)			ln(z a j )
	2
		b
			j 1	.	(7.68)

Здесь аj – комплексное число, определяющее положение стока за номером j.
В соответствии с формулой (7.47) комплексное число аj					можно представить в

тригонометрической форме, заменив в (7.47) z на аj, r на а (радиус батареи). Тогда формулу (7.68) можно переписать для кольцевой батареи из n скважин в следующем виде:

2 j

F(z)

cos

i sin

2 b j 1

(7.69)

n 1

2 j

ln a

cos

i sin

b j 0

n 1

2 j

i sin

2 j

ln a

cos

2 j

i sin

2 j

cos

где

Целая рациональная функция вида хп - 1

может быть представлена в виде

n 1

2 j

i sin

cos

j 0

(7.70)

Выражение, сходное с правой частью формулы (7.70) имеется под знаком

логарифма в (7.69). Таким образом, можно

представить

характеристическую

функцию

F (z)

(7.69)

виде:

ln z

F(z)

2 b

(7.71)

Согласно формулам (7.42) и (7.71) находим модуль массовой скорости фильтрации

u :

nG zn 1

nG r n 1ei (n 1)

nG r n 1

2 b zn an

2 b r n ein an

2 b r r

r n

(7.72)

где z = rei ; r1, r2, ..., rn – расстояния точки пласта от стоков O1, О2 , ...Оn– соответственно.

В центре кольцевой батареи r = 0. Из (7.72) следует, что скорость фильтрации u здесь равна нулю. Эти точки фильтрационного поля называются точками равновесия. При разработке залежей нефти в окрестностях таких точек образуются «застойные области» – «целики нефти».

114

vk.com/club152685050 | vk.com/id446425943

Зная положения точек равновесия в пласте, можно находить рациональные приемы для своевременной ликвидации целиков нефти. Одним из таких приемов является изменение режима работы скважин, заставляющее нефть целика прийти в движение в нужном направлении.

7.4.6. Подсчет времени движения частицы несжимаемой жидкости вдоль линии тока

Для однородной несжимаемой жидкости в выражениях характеристической функции потока F (z ) , потенциальной функции φ и функции тока ψ можно опустить постоянный множитель и вести расчеты применительно к объемному дебиту Q и скорости фильтрации u, а не к массовым дебиту G и скорости фильтрации u. Таким образом формулы (7.40) для проекции массовой скорости фильтрации на оси декартовых координат могут быть для несжимаемой жидкости применены к вычислению проекции скорости фильтрации на эти оси ux и uy:

Формула (7.41) для несжимаемой жидкости запишется в виде:

dF	u		iu
dz	u	x	iu	y
		x		y	.

Но проекции скорости движения на оси координат равны следовательно, можно записать

(7.73)

(7.74)

dx/dt и dy/dt,

u		m	dx	;	u
u	x	m	dt	;	u	y
	x					y

Исключаем из (7.73) ux и uy с помощью движения частицы в направлении осей x и у :

mdy dt

(7.75)

и интегрируя, получим уравнения

(x,

Чтобы

y) C

x		1		y		1
t m			dx ,	t m			dy.

x				y
	0	y			0	x

							(7.76)

вывести формулу времени движения частицы жидкости вдоль линии тока

,подставим значения ux и uy из (7.75) в формулу (7.74):

dF	m	dx idy	m	d(x iy)	m	dz	,
dz		dt		dt		dt
							(7.77)

где z=x-iy - сопряженное с z комплексное переменное.

Разделяя переменные в (7.77) и интегрируя вдоль линии тока, получим ф ормулу для подсчета времени движения частицы на длине кривой L:

t m 1 dx L dF

dz .

(7.78)

7.4.7. Стягивание контура нефтеносности к эксплуатационной кольцевой батарее

Имеется кольцевая батарея из n (n>2) эксплуатационных скважин, размещенных равномерно по окружности радиусом а. Контур питания удален от всех скважин на

115

vk.com/club152685050 | vk.com/id446425943

расстояние rк, значительно превышающее а. Первоначально контур нефтеносности представляет собой окружность, концентричную по отношению к окружности – батарее и имеющую радиус rн, причем rн в несколько раз меньше rк, но больше радиуса батареи

а.

Подсчет времени движения частиц контура нефтеносности по линиям тока проведем по формуле (7.78). При этом характери стическую функцию течения

определяем по формуле (7.71):

ln z

F(z)

2 b

(7.79)

где Q – объемный дебит одной из скважин.

Таким образом

n 1

2 b z

(7.80)

Величины z и z запишем в полярной системе координат:

z re

(7.81)

Тогда из (7.80) и (7.81) следует, что

nQ r

n 1

i (n 1)

2 b

i n

(7.82)

Рассматриваем движение частиц только вдоль прямых линий тока – главной и нейтральной (рис. 7.9). По всем главным линиям тока частицы контура нефтеносности движутся с одинаковой скоростью, по всем нейтральным линиям тока характер движения этих частиц также один и тот же. Поэтому достаточно найти время продвижения двух частиц контура: одной, которая движется по любой из главных линий тока, и другой, движущейся по любой из нейтральных линий.

Направим полярную ось из центра батареи вдоль одной из главных линий тока и будем искать время движения частицы контура нефтеносности вдоль полярной оси и по вдоль нейтральной линии, ближайщей к этой оси.

Так как для главных и нейтральных линий тока =const, можно на основании

второй формулы (7.81) определить dz следующим образом:

e i dr .

(7.83)

Подставляя значения dF/dz из (7.82) и dz из (7.83) в формулу (7.78), получим:

2 bm r

r n

e i an

r n 1

rн

(7.84)

где r/ – полярный радиус частицы.

Уравнение полярной оси имеет вид =0. Подставляя это значение в уравнение

(7.84), получим формулу для вычисления времени движения

частицы

контура

нефтеносности по главной линии тока:

2 bm

n 1

(7.85)

Уравнение нейтральной линии тока = /n. Подставим это значение в (7.78) и

заметим, что

e i cos i sin 1

Тогда уравнение

движения

частицы

контура нефтеносности по нейтральной линии тока представится в виде

116

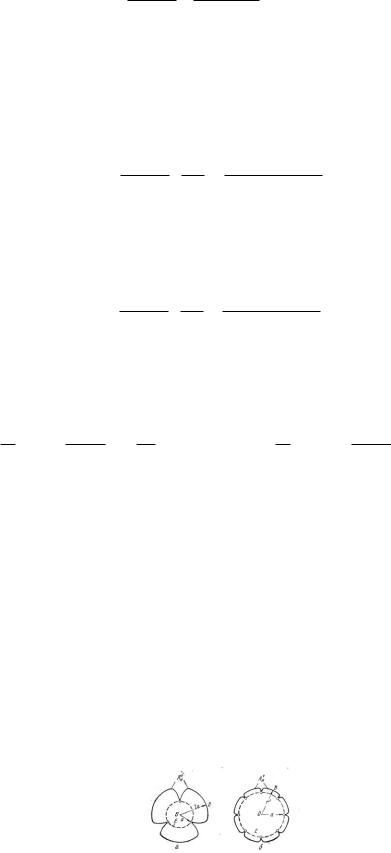
vk.com/club152685050 | vk.com/id446425943

t	2 bm	r	r	n	a	n
	2 bm		r		a	dr
	Qn			r	n 1	dr
	Qn	r			n 1
		r
		н				.	(7.86)
						.	(7.86)

Из частиц контура нефтеносности раньше всех других достигнут скважин те, которые движутся по главным линиям тока, так как их пути – наикратчайшие. Когда частица контура, движущаяся по главной линии тока, подойдет к скважине, последняя

начнет

обводняться. В

этот момент времени tn, в уравнении

(7.85) надо считать,

что

r a

. После интегрирования правой части (7 .64 ), получим

2 bm

(n 2)r n 2

(7.87)

Определим точку нейтральной линии тока, в которой будет находиться частица

контура

нефтеносности в момент начала обводнения скважин tn

для этого раскроем

интеграл правой части (7.86) и напишем это равенство для момента tn:

2 bm

(n 2)r n 2

(7.88)

Местоположение частицы контура нефтеносности на нейтральной линии тока в момент прорыва воды в скважины можно определить, приравняв правые части формул (7.87) и (7.88) и решив затем полученное уравнение n-степени относительно r'.

r	n					n 2			n 2
r			2		a			r		2	0
				2			1	1			0

a		n 2		rн				a		n 2
											. (7.89)
											. (7.89)

Исследуя уравнение (7.89), В. Н. Щелкачев установил, что величина r'/а возрастает с увеличением отношения rн/a; следовательно, чем больше величина радиуса первоначального контура нефтеносности, тем больше отставание точек контура нефтеносности, движущихся по нейтральной линии тока, от точек контура, движущихся по главной линии тока..

При величине радиуса контура нефтеносности rн более, чем в два раза превышающей радиус батареи а можно пренебрегать тем членом уравнения (7.89), который содержит множитель а/rн. Тогда уравнение (7.89) принимает более простой вид

r n

r n 2

n 2

2 a

(7.90)

При n= 3 уравнение (7.90) сводится к кубическому уравнению, у которого левая часть раскладывается на множители. К кубическому уравнению сводится (7.90) и при n = 6. Если n = 4, получим биквадратное уравнение, если n=8 – уравнение четвертой степени.

Ри с . 7 . 2 5 . К о н т у р н е ф т е н о с н о с т и в м о м е н т п р о р ы в а в о д ы в с к в а ж и н ы к о л ь ц е в о й б а т а р е и

117

vk.com/club152685050 | vk.com/id446425943

На рис. 7.25 контуры нефтеносности вычерчены для трех и восьми скважин в момент прорыва в них воды. Чем больше скважин в батарее, тем меньше отставание частиц контура нефтеносности от тех, которые движутся по главной линии тока, т. е. тем равномернее стягивается контур.

Исследования при помощи формул (7.85) и (7.86) позволяют утверждать, что формы контура нефтеносности, которая первоначально была в виде окружности, искажается лишь в ближайшей окрестности скважин. При анализе явления стягивания контура к скважинам кольцевой батареи допустимо применить «галереизацию», т. е.

кольцевую батарею заменить равнодебитной кольцевой галереей

Время безводной эксплуатации батареи tn определяется формулой (7 .87). Из этой же формулы легко определить: 1) общий объем добытой нефти за время безводной эксплуатации, 2) объем оставшейся в пласте нефти к начальному моменту обводнения скважин и 3) площадь, занятую оставшейся в пласте нефтью.

Действительно, общий объем добытой жидкости за время безводной эксплуатации скважин Qntn подсчитывается по формуле (7.87) следующим образом:

nQt

bm r

n 2

rн

(7.91)

Объем оставшейся в пласте нефти определится по формуле

n 2

m r

nQt

bma

n 2

rн

(7.92)

Наконец, площадь

ωн, занятая оставшейся в пласте нефтью в момент прорыва

воды в скважины, находим по формуле

nQtn

n 2

rн

(7.93)

Если сравнить площадь оставшейся в пласте нефти ωн

с площадью

круга,

ограниченного кольцевой

батареей скважин а2, получим значения отношения

ωн/ а2,

приведенные в таблице для а = 0,4rн и 0,1rн.

Из таблицы видно, что при большом числе скважин в батарее нефтеносная площадь ωн не зависит от величины отношения а/rн.

Относительное количество нефти, остающейся в пласте к моменту начала обводнения скважин кольцевой батареей

			Число скважин

а/rн.	4		8	∞
а/rн.
		Относительная величина площади
			ωн/ а2
0,4	1,84		1,33	1

0,1	1,99		1,33	1

118

vk.com/club152685050 | vk.com/id446425943

7.5. Метод конформного отображения

7.5.1. Общие положения

Ранее была установлена связь между теорией функций комплексног о переменног о и теорией плоских фильтрационных потоков.

Эта связь позволяет каждую функцию F (z) комплексного переменного z = х +iy трактовать, как поле некоторого плоского движения.

Введем новое комплексное переменное	i	, связанное со старым переменным z

соотношением z = z (ς), где z (ς) произв ольная аналитич еская функция.

Первое движение происходило на плоскости комплексного переменного z и характеризовалось комплексным потенциалом F (z). Подстав ляя вместо z его

выражение ч ерез ς получим
F(z) F[z( )] F	( )
1		,	(7.94)
		,	(7.94)

где F1 –новая функция.

Полученная из F функция F1 определяет некоторый плоский фильтрационный поток на плоскости ς и, изучив перв ый поток F, можно легко изучить поток F1

(ς).

Таким образом, задаваясь той или иной преобразующей функцией z = z (ς), из одного потока F (z) плоскости z можно получить бесчисленное множество других потоков на плоскости ς. Последнееозначает, что функция z=z(ς) реализует конформное отображение плоскости z на плоскость ς.

Для решения задач интерференции скважин в кач еств е исход ного потока удобно взять течение к скважине, эксцентрично расположенной в круговом пласте, являющееся вместе с тем течением между равнодебитными источником и стоком.

Применение метода конформног о отображения позв оляет полу чить решения ряда задач интерференции скважин значительно быстрее, нежели методами, основанными на прямой суперпозиции источников и стоков.

Метод конформных отображений в настоящее время широко применяется в о многих физических и технич еских задачах. При помощи этог о метода удается решить ряд плоских задач напорной и безнапорной фильтраций.

7.5.2. Вывод некоторых формул для притока к скважинам при помощи конформного отображения

Предположим , ч то на плоскости комплексного переменного z=х+iy дано некоторое теч ение с комплексным потенциалом F(z) . Введем новое

комплексное переменное i , связанное со старым переменным z

зависимостью z=z(ς) или ς=ς(z).		Отделяя в функции z=z(ς)действительную часть от
мнимой, получаем
z( ) z( i ) x( , ) iy( , )			,
			,
откуда x=x(ξ,η),	y=y(ξ,η),
ξ= ξ(x,y),	η= η(x,y).		(7.95)

Уравнения (7.95) устанавливают соответствие между точками плоскостей ς и z. В зависимости от того, однозначна или многозначна преобразующая функция z=z(ς) , каждой точке плоскости ς соотв етствует одна или несколько точек плоскости z.

Точно так же каждой линии одной плоскости соответствует одна или несколько линий на другой плоскости. Таким образом, линиям тока и эквипотенциалям, т. е. сетке течения одной плоскости, будет соответствовать вполне определенная сетка течения на

119

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 5813 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в предмете Добыча нефти и газа

#
14.08.20195.48 Mб75Насосная добыча нефти.pdf
#
17.08.2019461.5 Кб6Насосно-силовое оборудование.pdf
#
21.08.20198.76 Mб26Неотектоника лекции.pdf
#
21.08.20194.12 Mб9Нефтегаз-1.pdf
#
12.08.201966.81 Кб3нефтегаз.pdf
#
31.08.201919.68 Mб65Нефтегазовая гидромеханика.pdf
#
21.08.20194.64 Mб42НЕФТЕГАЗОВОЕ ОБОРУДОВАНИЕ.pdf
#
11.08.2019987.33 Кб10Нефтегазовый потенциал и перспективы освоения и развития.pdf
#
10.08.2019198.36 Кб6Нефтегазоносность фундаментов, кор выветривания.pdf
#
18.08.20193.62 Mб34Нефтегазоотдача пластов.pdf
#
21.08.20192.53 Mб17Нефтегазопромыслова...pdf