Авиационный колледж

ФГБОУ ВПО Рыбинский государственный авиационный технологический университет П. А. Соловьева

Реферат

по дисциплине:

"Информационные технологии в профессиональной деятельности"

На тему: "Закон аддитивности информации. Теорема Кательникова и ее применение. Формула Шеннона и ее применение"

Студент гр Ю21П

_______________

Руководитель

_______________

Рыбинск 2012год

Содержание:

Понятие аддитивности……………………………………………………………………………………………

Аддитивность в математике…………………………………………………………………………………..

Аддитивность в физике…………………………………………………………………………………………..

Аддитивность в химии………………………………………………….…………………………………………

Теорема Котельникова……………………………………………………………………………………..……..

История открытия…………………………………………………………………………………………………....

Развитие теоремы……………………………………………………………………………………………………

.

Теорема Шеннона……………………………………………………………………………………………………

Утверждение теоремы…………………………………………………………………………………………….

История развития…………………………………………………………………………………………………….

Критерий Найквиста………………………………………………………………………………………………..

Теоремы Шеннона для канала с шумами……………………………………………………………….

Теорема Шеннона — Хартли…………………………………………………………………………………..

Значение теоремы…………………………………………………………………………………………………..

Понятие Аддитивности

Аддитивность (лат. additivus — прибавляемый) — свойство величин, состоящее в том, что значение величины, соответствующее целому объекту, равно сумме значений величин, соответствующих его частям, в некотором классе возможных разбиений объекта на части. Например, аддитивность объёма означает, что объём целого тела равен сумме объёмов составляющих его частей.

Аддитивный (от лат. additio — прибавляю) — относящийся к сложению.

Аддитивность в математике

• Аддитивность площади (или объёма) означает, что площадь (или объём) фигуры равна сумме площадей её частей, если этих частей конечное число.

Если при этом допускается разбиение на счётное число частей, то это свойство называется σ-аддитивностью (сигма-аддитивностью).

• Аддитивные сет-функции и меры.

В теории чисел аддитивная функция — функция, определённая на натуральных числах и удовлетворяющая соотношению

Аддитивность в физике

В физике, аддитивность величины — когда величина чего-то равна сумме величин составных частей. Также такие величины называются экстенсивными, в отличие от интенсивных (например, температура и, как правило, плотность итп).

Примеры аддитивных величин:

• Энергия;

• Импульс;

• Энтропия;

• Количество вещества (в случае смеси не взаимодействующих химически ингредиентов);

• Мощность;

• Давление, плотность (в случае смеси идеальных газов);

• Электрический заряд;

• Мощность электрического тока;

Свойство аддитивности для некоторых, нередко векторных, физических величин называется принципом суперпозиции:

Напряжённость электрического поля, Напряжённость магнитного поля;

Электромагнитный потенциал;

в том числе в трехмерной формулировке электродинамики отдельно скалярный и векторный потенциалы электростатический потенциал;

Напряженность гравитационного поля и гравитационный потенциал в ньютоновской теории гравитации (в ОТО может выполняться только приближенно в пределе слабых полей);

Сила.

Часто термин принцип суперпозиции подразумевает аддитивность полей, создаваемых источниками, в свою очередь аддитивными, и применяется к теориям, основные уравнения которых линейны.

Некоторые величины, такие как масса, скорость (относительное движение) или время (последовательные интервалы), допускают сложение в классической физике, но не в теории относительности.

Вообще в случае высоких или сверхвысоких энергий аддитивность как правило рано или поздно теряется, поскольку уравнения перестают быть линейными (а линейными являются лишь их низкоэнергетические приближения), однако принцип суперпозиции бывает полезен почти всегда в пределе слабых возмущений, а иногда оказывается справедливым для всего или почти для всего практически доступного диапазона величин. Теория же в этом случае сильно упрощается и может быть легче и лучше развита.

Аддитивные свойства в химии

Согласно ЭСБЕ, если смешать два совершенных (трудно сжижаемых, имеющих низкую критическую температуру) газа, то объем смеси окажется почти математически точно равным сумме объёмов смешанных газов; точно так же не изменятся при смешении их светопреломляющая способность, удельная теплоёмкость и т. д., и эти свойства такой смеси могут быть вычислены на основании свойств смешиваемых тел. Не то наблюдается, когда смешиваются между собою жидкости: сумма их объёмов обыкновенно не равна (больше, меньше) объёму смеси и т. д.; но иногда и здесь оказывается возможным вычислить (с достаточной степенью приближения к опытным данным) некоторые свойства смеси из свойств слагаемых, руководствуясь только правилом смешения и предполагая, что эти свойства при смешении не меняются. Подобные свойства называются, согласно предложению Оствальда, аддитивными (ср. Ostwald, «Allg. Ch.», 2-е изд. 1-й т., 1120—1122 [1891]). Математически строго аддитивны только массы смешиваемых тел, но иногда аддитивные объёмы, и если V есть объём смеси, а V1, V2, и т. д. объёмы смешиваемых жидкостей (жидкостей и твёрдых тел), то

V = V1 + V2 + …,

а если смешиваются массы m1, m2, … и уд. объём (объём единицы массы) смеси есть v, а смешиваемых тел v1, v2 …, то

v(m1 + m2…) = v1m1 + v2m2 +…

или v = v1[m1/(m1 + m2)] + v2[m2/(m1 + m2)] +…;

иногда А. теплоёмкость смеси, и в таком случае с (уд. теплоёмкость смеси)

с = c1[m1/(m1 + m2)] + c2[m2/(m1 + m2)] + …,

где с1 и с2 уд. теплоёмкости смешиваемых тел, имеющих массы m1 и m2, или же, так как

(100m1)/(m1 + m2) = p,

процентному содержанию в смеси тела с массой m1, то

с = c1(p/100) + c2[(100 — p)/100]

В теории растворов, начиная с XIX века аддитивность свойств рассматривается, как обоснованная электролитической диссоциацией растворённых солей[1].

Аддитивные методы в фотографии

Методы получения цветных изображений, основанные на аддитивном синтезе цветов. Методы цветной фотографии#Аддитивные методы

Аддитивные величины в быту и в экономике

Примером аддитивной величины можно считать деньги и другие материальные ценности, подлежащие количественному учету, а также рабочее время итд (хотя эффект их применения вообще говоря не аддитивен).

Теорема Котельникова

Теорема Котельникова (в англоязычной литературе — теорема Найквиста — Шеннона или теорема отсчётов) гласит, что, если аналоговый сигнал имеет финитный (ограниченный по ширине) спектр, то он может быть восстановлен однозначно и без потерь по своим дискретным отсчётам, взятым с частотой строго большей удвоенной верхней частоты :

Такая трактовка рассматривает идеальный случай, когда сигнал начался бесконечно давно и никогда не закончится, а также не имеет во временно́й характеристике точек разрыва. Именно это подразумевает понятие «спектр, ограниченный частотой ».

Разумеется, реальные сигналы (например, звук на цифровом носителе) не обладают такими свойствами, так как они конечны по времени и, обычно, имеют во временно́й характеристике разрывы. Соответственно, их спектр бесконечен. В таком случае полное восстановление сигнала невозможно и из теоремы Котельникова вытекают 2 следствия:

• Любой аналоговый сигнал может быть восстановлен с какой угодно точностью по своим дискретным отсчётам, взятым с частотой , где — максимальная частота, которой ограничен спектр реального сигнала.

• Если максимальная частота в сигнале превышает половину частоты дискретизации, то способа восстановить сигнал из дискретного в аналоговый без искажений не существует.

Говоря шире, теорема Котельникова утверждает, что непрерывный сигнал можно представить в виде интерполяционного ряда

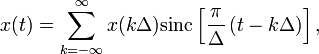
Где — функция sinc. Интервал дискретизации удовлетворяет ограничениям Мгновенные значения данного ряда есть дискретные отсчёты сигнала