1. Деление нормализованных двоичных чисел

Действительное число, записанное в прямом коде в формате, включающем позиций целой части называют нормализованным, если позиция старшего значащего разряда содержит цифру отличную от нуля. К нормализованным числам условно относят число ноль, содержащее во всех значащих разрядах цифру 0.

Например, десятичные числа в прямом коде 020310; 1143; 05670 и двоичные числа в прямом коде 110100; 011101; 11001 нормализованные, так как цифры в позициях старшего разряда не равны нулю. Десятичные 0020310; 100143; 005670 и двоичные 001011100; 1001110100; 101001 числа не нормализованы, поскольку позиции старшего значащего разряда содержат ноль.

Деление нормализованных чисел выполняют при делении операндов в формате с плавающей точкой. Деление нормализованных чисел можно выполнить любым рассмотренным выше способом. Однако поскольку частное от деления нормализованных чисел не равных нулю удовлетворяет условию вычислять разряды целой части частного, кроме младшего, не имеет смысла. Для этого достаточно сразу расположить операнды в исходной позиции в таком положении, которое они заняли бы при вычислении младшего разряда целого.

Рассмотрим деление нормализованных чисел на примерах.

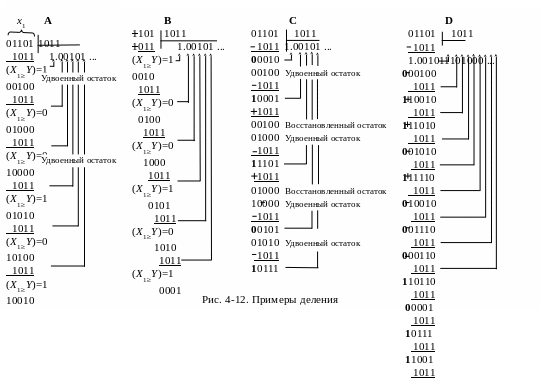
Пример 4-70. В вариантах A-D (рис.4-12) используются те же приемы деления, что и в примерах 4-67, 4-68, 4-65, 4-66 соответственно.

В варианте A в исходном состоянии делимое 1101 расширяют на один разряд, приписывая нуль слева, и размещают младшие разряды делимого и делителя в одной позиции. В дальнейшем остатки, сдвинутые на разряд влево с занесением нуля справа (удвоенные), записывают на место делимого, а результаты сравнения фиксируют в частном.

Так как в первом шаге делимое оказалось больше делителя разряд целого в частном 1, а остаток равен их разности 00010. Удвоенный остаток, записанный на место делимого 00100. Так как вычисленный удвоенный остаток меньше делителя новый результат сравнения , а новый удвоенный остаток 00100 равен предыдущему остатку 00010, сдвинутому на разряд влево.

Если предыдущий удвоенный остаток больше делителя, в частное заносят 1, а на место делимого записывают удвоенную разность предыдущего остатка и делителя. В противном случае в частное записывают 0, а предыдущий остаток сдвигают влево.

Если старший разряд удвоенного остатка 1, можно не выполнять сравнение, так как его результат очевиден. Нет необходимости вычислять старший разряд разности и перенос в старший разряд, так как при записи удвоенного остатка они будут отброшены. Это не приведет к ошибке, поскольку остаток не может превышать делитель.

В варианте B каждый очередной разряд частного и остаток вычисляет очередной работник (вычислитель) предназначенный специально для этой цели. Вычисленный остаток он передает последующему вычислителю.

Первый вычислитель отличается от остальных. Он игнорирует при сравнении и вычитании зачеркнутые в примере старшие разряды делимого и делителя, так как нормализованные операнды всегда содержат в старшем разряде 1, и поэтому результаты сравнения и вычитания от них не зависят. Первый вычислитель передает второму вычислителю при делимое, включая старший зачеркнутый разряд, или при разность делимого и делителя, т.е. остаток. Передаваемая разность всегда содержит в старшем разряде 0. Поэтому вычисляют только остальные разряды разности, приписывая к ним слева 0.

Второй и последующие вычислители идентичны. Они смещают делитель на разряд вправо относительно полученного остатка, выполняют их сравнение и вычитание и передают очередному вычислителю новый остаток.

Конструктор вычислителя, должен учитывать, что младший разряд уменьшаемого и старший разряд вычитаемого всегда равны нулю (поэтому в примере B они заданы по умолчанию). Так как вычисляемый остаток не может быть больше делителя, то при вычитании можно игнорировать старший разряд операндов и не вычислять заем в старший разряд. По этой же причине при нет надобности пересылать последующему вычислителю старший разряд предыдущего остатка. Если старший разряд полученного остатка 1, то сравнение остальных разрядов можно не выполнять, так как результат сравнения очевиден.

Последний вычислитель должен выполнять только сравнение, так как очередной остаток не нужен.

В варианте C выполняется деление с восстановлением остатка и с сохранением его на месте делимого. Делимое расширяется на разряд влево с занесением 0. Это необходимо сделать, чтобы образовать позицию для записи на место делимого удвоенного остатка иногда содержащего в этом разряде 1.

В примере в каждом шаге вычисляют разность удвоенного остатка (в первом шаге его роль исполняет делимое) и делителя. Разность записывают на место предыдущего остатка, а инверсию ее знака (в примере знак выделен жирным шрифтом) – в разряд частного. Предыдущий остаток стирается.

Если знак разности 0, то она является остатком, и для получения нового удвоенного остатка последний сдвигают на разряд влево

Если знак разности 1, то она не является остатком. Для получения нового остатка нужно восстановить потерянный остаток. Для восстановления остатка к разности прибавляют делитель и записывают полученный старый остаток на место разности. Затем остаток сдвигают влево для его удвоения.

В варианте D выполняется деление способом без восстановления остатка и с сохранением удвоенной разности на месте делимого.

В исходном состоянии делимое расширено нулем в старшем разряде.

Из предыдущей удвоенной разности (в первом шаге ее роль исполняет делимое) вычитают делитель, если ее знак 0, или к предыдущей удвоенной разности прибавляют делитель, если ее знак 1. Результат вычитания (сложения) записывают на место предыдущей разности со сдвигом на разряд влево. При записи инверсию знака (в примере знак выделен жирным шрифтом) сохраняют в частном, а значащие разряды, дополненные нулем справа – на месте делимого. Таким образом, о знаке предыдущей разности судят по значению последней вычисленной цифре частного. В исходном состоянии ее принимают равной 1.

Операции вычитания делителя можно заменить операциями сложения с дополнением делителя.