1. Сокращение матриц дополнительных кодов частных произведений

Трудоемкость вычислений, затраты времени и средств, вероятность ошибок и другие показатели эффективности зависят от:

• размерности матрицы частных произведений;

• количества нулевых строк;

• количества нулей в строке;

• типа и способа выполнения операций над строками и/или столбцами для вычисления произведения;

• способа вычисления частных произведений;

• системы счисления, в которой представлены операнды и результат.

Этот перечень можно продолжить.

В данном подразделе рассматриваются некоторые способы преобразования матриц дополнительных кодов частных произведений упрощающие вычисления. Они могут применяться независимо от того, каким именно способом матрицы вычислены.

1. Знаковый разряд дополнительного кода произведения можно вычислять по отдельному правилу (раздел 4.4.2). Это позволяет сократить левый столбец матрицы.

2. Старший значащий разряд дополнительного кода положительного произведения равен 1, только если код обеих операндов 1|00…0_доп. При отрицательном произведении он всегда равен 1 (раздел 4.4.2). Это позволяет старший разряд произведения вычислять по отдельному правилу и сократить второй столбец слева в матрице частных произведений (например, в примере 4-32 варианты E и F).

3. Вычисление произведения по отдельным правилам при операндах равных 0 и/или 1|00…0_доп (раздел 4.4.2) исключает умножение в столбик при этих операндах (пример 4-27) и строку в матрице при умножении на при иных значениях операндов (примеры 4-32, 4-34).

4. Если код 1|00…0 не применяется для кодирования числа , отпадает необходимость вычисления старшего значащего разряда, так как количество значащих разрядов в произведении будет (раздел 4.4.2). Исключение кода 1|00…0 из списка применяемых для кодирования чисел упрощает умножение.

5. В разделах 4.4.2.1 - 4.4.2.10 описаны разные способы умножения, причем в одних случаях строки матрицы складывались, в других вычитались из нуля, а например, в примерах 4-37 и 4-39 одни строки суммируются, другие вычитаются. В строках матрицы бывает записан код множимого или код множимого с обратным знаком , например в примере 4-45.

При реализации любого способа умножения следует учитывать взаимозаменяемость операций сложения и вычитания (раздел 4.3.7), выполняемых над строками матрицы. Для изменения операции достаточно изменить знак частного произведения записанного в строке. Напротив, можно изменить знак частного произведения, заменив операцию, выполняемую над строкой, обратной ей. Если учесть, что существует множество способов изменения знака числа в дополнительном коде, то у каждого способа умножения существует множество модификаций. Конструктор системы умножения должен выбрать не только способ умножения, а и целесообразную в его применении модификацию.

6. Расширение частных произведения влево цифрой 0 или обратной нулю существенно усложняет выполнение сложений/вычитаний строк матрицы при некоторых способах организации процесса вычислений, например при параллельном (матричном). Можно сократить количество расширяющих цифр и придать матрице форму подобную той, которая имеет место при умножении в прямом коде, воспользовавшись свойствами треугольной или трапецеидальной матрицы, образованной расширяющими цифрами и цифрой знака ¹⁰.

Рассмотрим свойства треугольной и трапецеидальной матрицы.

Пусть, например, треугольные матрицы в системах счисления с и имеют вид, показанный на рис.4-1. Их ненулевые строки содержат цифры обратные нулю. Жирным шрифтом показан столбец кода знака частных произведений в алфавите {0, 1}.

Утверждение 1. Результат вычитания из нуля строк треугольной матрицы, расширяющей влево дополнительные коды частных произведений, равен строке, образованной поворотом по часовой стрелке столбца знаков частных произведений в алфавите {0, 1}.

Утверждение 2. Сумма строк треугольной матрицы, расширяющей влево дополнительные коды частных произведений, равна дополнению строки, образованной поворотом по часовой стрелке столбца знаков частных произведений в алфавите {0, 1}.

Предоставим Читателю возможность самостоятельно доказать справедливость утверждений 1 и 2. В их справедливости можно убедиться на примерах, в том числе на примерах, приведенных на рис.4-1.

Результаты вычитания строк матриц из нуля по правилу вычитания дополнительных кодов в соответствующих системах счисления являются строками, содержащими цифры 0 и 1. Под строками разностей приведены их дополнения в десятичной и двоичной системе счисления соответственно.

Поворот строк разности на 90^о против часовой стрелки образует столбцы, показанные на рис.4-1 жирным шрифтом. Цифры в столбцах являются кодами знаков соответствующих частных произведений в алфавите {0,1}. Это свойство треугольной матрицы не зависит от основания системы счисления.

Результат сложения строк треугольной матрицы по правилу сложения дополнительных кодов является дополнением строки разности, что следует из их сопоставления. Это свойство треугольных матриц так же не зависит от основания системы счисления.

В некоторых случаях, например в примере 4-32 варианты A и B, матрица, расширяющая влево дополнительные коды частных произведений, является трапецеидальной. Примеры таких матриц приведены на рис.4-2.

З десь трапецеидальные матрицы ограничены снизу горизонтальными линиями, под которыми жирным шрифтом условно добавлены строки содержащие нули, чтобы придать матрицам треугольную форму. Приписывание нулевых строк не может изменить результаты сложения или вычитания из нуля строк трапецеидальных матриц.

Поскольку результаты сложения и вычитания из нуля строк трапецеидальной и треугольной матриц совпадают, то на основании Утверждений 1 и 2 можно сформулировать следующие утверждения.

Утверждение 3. Результат вычитания из нуля строк трапецеидальной матрицы равен строке, образованной поворотом по часовой стрелке столбца знаков частных произведений в алфавите {0, 1}, расширенной слева нулями до требуемого количества разрядов.

Утверждение 4. Сумма строк трапецеидальной матрицы равна дополнению строки, образованной поворотом по часовой стрелке столбца знаков частных произведений в алфавите {0, 1}, расширенной слева цифрами обратными нулю до требуемого количества разрядов.

Цифры, расширяющие результат вычитания и сумму строк, показаны на рис.4-2 жирным шрифтом.

Утверждения 1-4 справедливы при представлении чисел в системах счисления с основанием и алфавитом цифр .

Преобразования матриц дополнительных кодов частных произведений, использующие описанные свойства, рассмотрим на примерах.

Пример 4-56. Операнды в двоичном дополнительном коде имеют значащих разряда. Код 1|0000_д применяется для кодирования числа .

В варианте A выполнено умножение множимого на с вычислением всех разрядов произведения, включая разряд знака. Так как , частные произведения суммируются. Матрица, содержащая разряды знака, трапецеидальная и показана жирным шрифтом.

Воспользовавшись Утверждением 4, вычислим сумму строк трапецеидальной матрицы. После поворота левого столбца по часовой стрелке получим строку 01010, которую следует расширить одним нулем слева. После расширения получим строку 001010. Ее дополнение 110110 равно сумме строк трапецеидальной матрицы.

В варианте B трапецеидальная матрица заменена суммой ее строк показанной жирным шрифтом. Разумеется, что такое преобразование не может изменить сумму строк матрицы частных произведений.

В варианте C разряды суммы строк трапецеидальной матрицы кроме младшего опущены вниз и приписаны к значащим разрядам частных произведений. Очевидно, что и это преобразование не может изменить сумму строк матрицы частных произведений.

Сравним построчно левый столбец матрицы в варианте A с разрядами, показанными жирным шрифтом, в матрице варианта C. В варианте C к значащим разрядам частных произведений на два младших разряда приписаны их знаки, а к остальным частным произведениям приписаны инверсии их знаков. Почему так?

Ответ на этот вопрос вытекает из анализа выполненных преобразований. Код, выделенный в матрице варианта C жирным шрифтом, является дополнением кода знаковых разрядов левой колонки матрицы варианта A.

Если все строки матрицы частных произведений вычитаются из нуля, то треугольная или трапецеидальная матрица должна быть заменена суммой ее строк, поскольку именно сумму строк необходимо вычитать из нуля при вычислении произведения. Из этого следует, что правило приписывания дополнительных разрядов к значащим разрядам частных произведений не зависит от того сложение или вычитание строк матрицы выполняется при вычислении произведения. Вариант D примера 4-56 иллюстрирует это свойство. Здесь по сравнению с вариантами A, B и C изменен только знак множителя, и поэтому вместо сложения выполняется вычитание частных произведений.

В варианте E операнды те же, что и в варианте D, и вычисление произведения выполняется тем же способом, но принято решение о замене операции вычитания частных произведений сложением. Для этого частные произведения вычислены со знаком обратным знаку множимого, и все они имеют код знака 0. Дополнительный код колонки знака равен 00…0. Поэтому к частным произведениям приписаны слева нули.

Пример 4-57. В вариантах A-C операнды в десятичном дополнительном коде и имеют значащих разряда. Код 1|0000_д применяется для кодирования числа .

В варианте A выполнено умножение множимого на с вычислением всех разрядов произведения, включая разряд знака. Так как , частные произведения суммируются. Матрица, расширяющая частные произведения, треугольная и показана жирным шрифтом.

В варианте B дополнительный код разрядов знака частных произведений приписан к значащим разрядам подобно тому, как это сделано в варианте C примера 4-56.

В варианте C по сравнению с вариантами A и B изменен только знак множителя, и вместо сложения выполняется вычитание частных произведений.

В варианте D операнды те же, что и в варианте C, и вычисление произведения выполняется тем же способом, но принято решение о замене операции вычитания частных произведений сложением. Для этого частные произведения вычислены со знаком обратным знаку множимого, и все они имеют код знака 0. Дополнительный код колонки знака равен 00…0. Поэтому к частным произведениям приписаны нули слева.

При записи частных произведений с сокращенной треугольной или трапецеидальной матрицей приписывание дополнительных разрядов требует вычисления дополнения колонки разрядов знака. Это можно делать, применяя различные правила

1⁰. К значащим разрядам дополнительного кода частного произведения на младший разряд множителя следует приписывать слева 0, если его знак (+), иначе цифру обратную нулю.

Если ко всем предыдущим частным произведениям на младшие разряды множителя приписаны нули, к значащим разрядам очередного частного произведения следует приписывать слева 0, если его знак (+), иначе цифру обратную нулю.

Если хотя бы к одному предшествующему частному произведению приписан не 0, то к очередному частному произведению следует приписать цифру обратную 0, если его знак (+), иначе цифру меньшую обратной 0 на 1.

Если ширина матрицы после записи частных произведения на все разряды множителя меньше длины формата произведения, то частное произведение на старший разряд множителя следует расширить до формата произведения, приписывая слева нули, если ко всем частным произведениям, включая последнее, приписаны 0, иначе цифры обратные нулю.

В справедливости этого правила можно убедиться на примерах 4-56 и 4-57.

2⁰. Ко всем частным произведениям, кроме произведения на младший разряд множителя, приписать цифру обратную 0, если его знак (+), иначе приписать цифру обратную 1. К частному произведению на младший разряд множителя приписать пару цифр 10, если его знак (+), иначе приписать 0 и цифру обратную нулю.

Если ширина матрицы после записи частного произведения на все разряды множителя меньше длины формата произведения, то частное произведение на старший разряд множителя следует расширить до формата произведения, приписывая к нему цифры обратные 0.

Правила 1⁰ и 2⁰ справедливы, если над всеми строками матрицы выполняются одинаковые операции.

Примеры 4-58 и 4-59 иллюстрируют применение правила 2⁰.

A B С D

X: 1|2375_д (-7625) 1|2375_д 1|2375_д (-7625) 1|2375_д

Y: 0|1070 _д 1|8930 _д (-1070) 0|1069 _д 1|8931 _д (-1069)

+ 1000000 – 1000000 + 0931375 – 0931375

+ 846625 – 846625 + 854250 – 854250

+ 900000 – 900000 + 900000 – 900000

+ 892375 – 892375 + 892375 – 892375

+ 900000 – 900000 + 900000 – 900000

9991841250 _д 0008158750_д 9991848875 _д 0008151125_д

– 008158750 + 008158750 – 008151125 + 008151125

Пример 4-58. Умножение дополнительных кодов десятичных чисел выполняется тем же способом, что и в примере 4-57, но дополнительные разряды приписаны к частным произведениям по правилу 2⁰.

Пример 4-59. Умножение дополнительных кодов двоичных чисел выполняется тем же способом, что и в примере 4-56, но дополнительные разряды приписаны к частным произведениям по правилу 2⁰.

A B C D E

X: 1|1010_д (-6) 1|1010_д (-6) 1|1010_д (-6) 1|1010_д (-6) 1|1010_д (-6)

Y: 0|1010 _д (+10) 1|0110 _д (-10) 0|1011 _д (+11) 1|0101 _д (–11) 1|0000 _д (–16)

100000 – 100000 + 011010 – 011010 – 100000

01010 – 01010 + 01010 – 01010 – 10000

10000 – 10000 + 10000 – 10000 – 10000

01010 – 01010 + 01010 – 01010 – 10000

110000 – 110000 + 110000 – 110000 – 101010

1111000100_д 0000111100_д 1110111110 _д 0001000010 _д 0001100000_д

-60 +60 -66 +66 +96

Способ сокращения треугольной и трапецеидальной матрицы и правила приписывания дополнительных разрядов к частным произведению справедливы в случае замены операции над строками матрицы обратной ей путем изменения знака частного произведения и применения обратного кода, как это изложено в разделах 4.4.2.11 и 4.4.2.12.

В некоторых случаях матрица, расширяющая частные произведения, не является треугольной или трапецеидальной. Например, в примере 4-55 в вариантах C-F двойки строк каждого частного произведения имеют одинаковое количество разрядов расширения показанных жирным шрифтом. В этом случае можно матрицу расширения декомпозировать на две треугольные матрицы. В одну из них входят разряды расширения, приписанные к строкам переносов, а в другую – приписанные к строкам младших разрядов частных произведений. Каждую матрицу независимо от другой можно сократить по правилам 1⁰ или 2⁰.

Пример 4-60. Операнды в десятичном дополнительном коде имеют значащих разряда. Код 1|000_д применяется для кодирования числа . Поэтому разрядность произведения . В обоих вариантах вычисляются все 8 разрядов произведения, включая разряд знака.

В вариантах A и B применен способ умножения (раздел 4.4.2.2). Поскольку , выполняется вычитание частных произведений из нуля. Чтобы заменить вычитание сложением, знак частных произведений изменен. Для этого вычислен их обратный код, и в матрицу введена верхняя строка 01221, дополняющая обратные коды до дополнительных.

Поскольку в системах с произведение цифры на цифру содержит 2 разряда, то частное произведение представлено парой строк. Верхняя строка пары содержит цифры старших, а нижняя – младших разрядов произведений цифры на цифру. Кроме того, в таблице умножения результат записан в обратном коде. Например, . Поэтому частное произведение на младший разряд множителя содержит в верхней строке 9222, а в нижней 9777. Так как обе строки представлены в обратном коде, то каждая из них должна быть дополнена 1 в строке дополнения. Если в столбце размещены младшие разряды двух строк требующих дополнения 1, то верхняя строка должна иметь в этом столбце 2. Вот почему в верхней строке код 01221.

В

A B

X: 0|999_д (+999) 0|999_д (+999)

Y: 1|602 _д (-398) 1|602 _д (-398)

01221 01221

9999222 9222

99999777 99777

999111 + 8111

9999888 89888

99777 8777

999222 89222

0000 9000

00000 90000

99602398_д 99602398_д

-397602

варианте A умножение выполнено без сокращения треугольных матриц. При этом обратные коды отрицательных частных произведений расширены влево цифрами обратными нулю (9), а положительные (0).

В вариантах A и B частное произведение равное 0 представлено кодом (+0). Если его представить кодом (–0), то две нижние строки матрицы изменят значение на 1111 и 11111. Кроме того, для их дополнения 1 придется изменить код в строке дополнения на 12221.

Разряды, расширяющие строки частных произведений образуют две матрицы. Матрица, расширяющая строки переносов показана курсивом. Матрица, расширяющая строки младших разрядов произведений цифры на цифру показана жирным шрифтом. Обе матрицы треугольные. Каждая из них может быть заменена суммой ее строк независимо от другой.

В варианте B для сокращения матриц применено правило 1^о.

При малой разрядности операндов эффективность способа сокращения не достаточно наглядна. C ростом разрядности операндов n количество сокращаемых цифр возрастает пропорционально .

При умножении на два разряда множителя (разделы 4.4.2.8 – 4.4.2.10, примеры 4-44 – 4-47) матрица, расширяющая частные произведения, не является треугольной или трапецеидальной, так как каждая очередная строка короче предыдущей не на 1, а на 2 разряда. Для сокращения подобной матрицы достаточно сделать ее треугольной или трапецеидальной, вставив между строк матрицы строки констант равных нулю, как это сделано в примере 4-61.

Пример 4-61. В варианте A выполнено умножение дополнительных кодов двоичных чисел на два разряда множителя способом, описанным в разделе 4.4.2.9.

М атрица, расширяющая частные произведения, не является треугольной или трапецеидальной.

В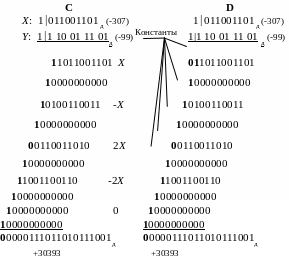 варианте B выполнена вставка в матрицу варианта A строк содержащих константы 0. Очевидно, что подобная вставка не может изменить значение произведения при любой операции выполняемой над строками матрицы, но теперь расширяющая матрица стала треугольной, и для ее сокращения можно применить правила 1⁰ или 2⁰.

В варианте C выполнена замена треугольной матрицы по правилу 1⁰, а в варианте D по правилу 2⁰.

В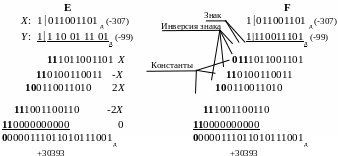 варианте C можно зачеркнуть строки констант 0, а приписанные к ним цифры (0 или 1) сместить в предшествующие строки. В варианте E приведен результат этого преобразования. Очевидно, что замена исходной матрицы (вариант A) матрицей в варианте E не может изменить значение произведения при любой операции выполняемой над строками матрицы.

На основании правила 1⁰ можно сформулировать правило приписывания дополнительных разрядов к частным произведениям при умножении дополнительных кодов двоичных чисел на два разряда множителя.

3⁰. К значащим разрядам дополнительного кода частного произведения на двойку младших разрядов множителя следует приписывать слева 00, если его знак (+), иначе 11.

Если ко всем предыдущим частным произведениям приписаны нули, к значащим разрядам очередного частного произведения следует приписывать слева 00, если его знак (+), иначе 11.

Если хотя бы к одному предшествующему частному произведению приписан код 11, то к очередному частному произведению следует приписать 11, если его знак (+), иначе 00.

Если ширина матрицы после записи частных произведений на все разряды множителя меньше длины формата произведения, то частное произведение на старший разряд множителя следует расширить до формата произведения, приписывая слева нули, если ко всем частным произведениям, включая последнее, приписаны 0, иначе единицы.

В варианте D примера 4-61 можно зачеркнуть константы 0, а приписанные к ним константы 1 сместить в предшествующие строки. В верхней паре строк константу 1 нужно сложить с инверсией знакового разряда частного произведения на двойку младших разрядов множителя. Сложение приведет к замене инверсии знака цифрой знака и к образованию переноса равного инверсии знака в следующий разряд. В варианте F приведен результат преобразования матрицы варианта D.

Исходя из анализа преобразования матрицы варианта A в матрицу варианта F и правила 2⁰, сформулируем правило приписывания дополнительных разрядов к частным произведениям при умножении дополнительных кодов двоичных чисел на два разряда множителя.

4⁰. К значащим разрядам дополнительного кода частного произведения на двойку младших разрядов множителя следует приписывать слева 100, если его знак (+), иначе 011. К остальным частным произведениям следует приписывать слева 11, если их знак (+), иначе 10.

Если ширина матрицы после записи частного произведения на все разряды множителя меньше длины формата произведения, то частное произведение на старший разряд множителя следует расширить до формата произведения, приписывая к нему 1.

При любом способе умножения на два разряда множителя конструктор может применить правило 3⁰ или 4⁰, если все строки матрицы суммируются или вычитаются.