1. Деление без восстановления остатка

Восстановление остатка существенно осложняет и замедляет процесс деления. Можно исключить восстановление остатка, если по известному отрицательному значению вычислять очередную разность .¹² Это можно сделать, прибавив делитель к сдвинутой влево отрицательной разности.

Рассмотрим деление с восстановлением остатка на примере 4-66.

П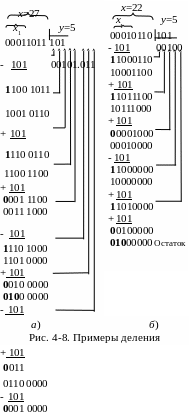 ример 4-66. Значения делимого и делителя на рис.4-8а такие же, как в примере 4-65. Приведем делимое и делитель к форматам аналогичным принятым в примере 4-65.

Выполним вычитание делителя из с записью разности на место , как это делали в примере рис.4-7. Сдвинем вычисленный код на разряд влево с занесением нуля справа (удвоим). Одновременно запишем в старший разряд частного инверсию знака разности, выделенного в примере жирным шрифтом. На месте получим код 10010110.

В следующем шаге, поскольку предыдущая разность отрицательна или вычисленный разряд частного равен 0, прибавим делитель для получения новой разности. Получим на месте код 11100110. Сравните его со значением разности при вычислении в примере 4-65 рис.4-8.

Во всех последующих шагах, в зависимости от значения вычисленной в предшествующем шаге цифры частного, выполняют сложение или вычитание делителя.

При делении целых с выделением целого частного и остатка (рис.4-8б) следует учитывать, что при последняя вычисленная разность отрицательна и не является остатком. В этой ситуации для получения остатка необходимо прибавить к ней делитель, как это показано на рис.4-8б на примере деления 22:5.

При делении целых с выделением целого частного и остатка можно вычисленную цифру частного записывать в позицию младшего разряда делимого. Для этого при сдвиге разности вправо следует выдвигать инверсию ее знака в освобождающуюся позицию младшего разряда. Тогда после завершения деления в младших позициях расширенного формата делимого будет записано частное, а в старших позициях расположен остаток.

Деление с восстановлением остатка позволяет исключить шаг восстановления остатка и тем самым уменьшить количество шагов и затраты времени на вычисление цифры частного. Однако для вычисления одной цифры частного необходимо выполнить два шага (сложить или вычесть и затем сдвинуть).

1. Деление с вычислением очередного сдвинутого влево остатка

Рассмотрим способ деления на примере.

Пример 4-67. Пусть ; . Количество разрядов в делимом ; в делителе – . Индексы старших разрядов частного и делимого равны . Вычислим разряды частного от до . Тогда ; .

Из (4-26) следует, что значение разряда равно значению отношения . Для его вычисления необходимо сравнивать предыдущий остаток с делителем, сдвинутым при на разрядов влево, а при на разрядов вправо.

При остаток , а делитель сдвинут на разрядов влево так, что младший значащий разряд делителя совмещен со старшим разрядом делимого в одной позиции.

Из (4-24) следует, что при очередной остаток равен предыдущему, а при очередной остаток равен .

Исходя из сказанного, выполним следующие действия.

Расширим формат делимого, приписав к нему слева нулей.

Разобьем формат расширенного делимого на две группы разрядов, старшую и младшую. К старшей группе (обозначим ее ) отнесем разрядов (рис.4-9).

Деление будем выполнять по шагам.

“Наймем трех работников – вычислителей”, которые будут, действуя одновременно и параллельно, выполнять в каждом шаге каждый свою работу.

1. Должен сравнивать количественные эквиваленты и , вычисляя значение отношения 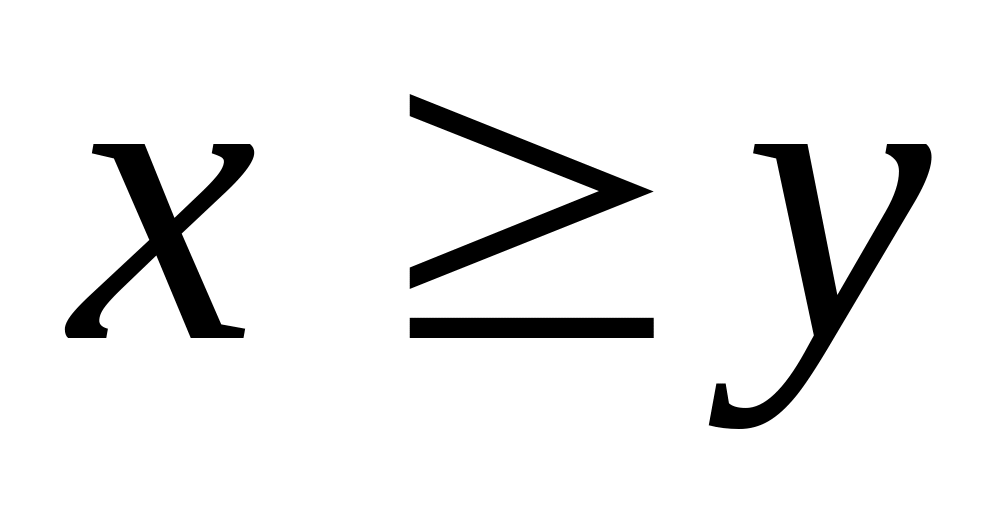, и заносить результат сравнения в разряд частного. При этом он сравнивает 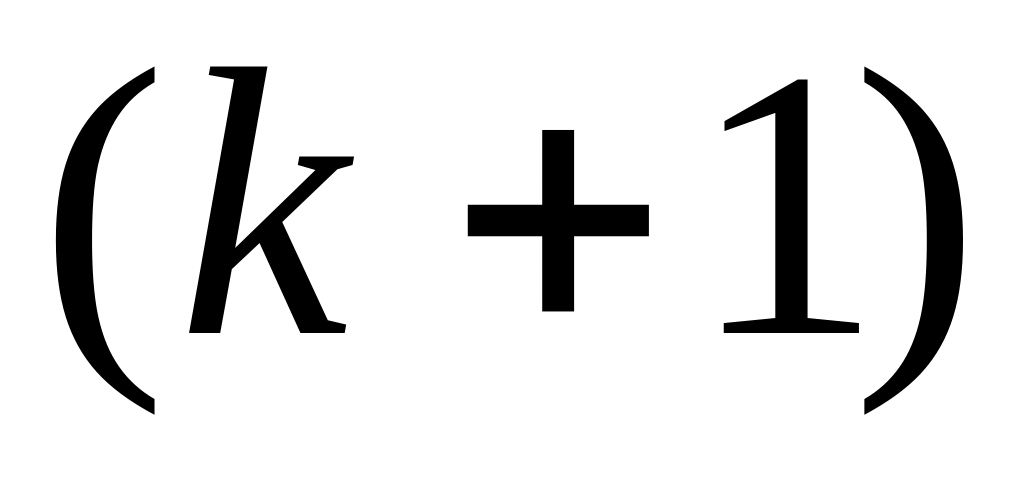разрядный код с разрядным кодом .

2. Должен вычислять значение разности .

Результат вычисления разности служит для определения очередного остатка и используется только в том случае, когда отношение , т.е. при . Поэтому можно разрешить: выполнять вычитание с ошибкой при ; вычислять только младших разрядов разности . Это позволит упростить и ускорить выполнение операции вычитания.

3. Должен записывать новый остаток, сдвинутый на 1 разряд влево, на место предыдущего остатка, передавая тем самым первому и второму работникам очередное новое для них исходное данное. Вначале предыдущий остаток равен расширенному делимому.

Новый остаток следует принять равным старому остатку, если первый работник вычислил 0. В противном случае для получения нового остатка следует к разности вычисленной вторым работником приписать справа младших разрядов предыдущего остатка (в данном примере 4 разряда).

Действительно. При очередной остаток равен предыдущему (4-24). Из (4-26) и (4-24) следует, что в очередном шаге следует повторить вычисления, сдвинув делитель на один разряд вправо по отношению к его положению в предыдущем шаге или, это то же самое, сдвинув делимое на разряд влево. При младшие разряды очередного остатка совпадают с младшими разрядами предыдущего остатка не участвовавшими в вычислениях, а старшие – равны разности вычисленной вторым работником. Поэтому при для получения очередного делимого нужно сдвинуть старое делимое на разряд влево с одновременной заменой старших разрядов вычисленной разностью. Поскольку при сдвиге старший разряд разности будет потерян, то нет смысла его вычислять, что учтено при вычислении .

В аппаратуре запись нового сдвинутого остатка на место старого, т.е. на место делимого в первом шаге, позволяет использовать в очередном шаге оборудование, выполнявшее сравнение и вычисление нового делимого в предыдущем шаге.

В примере рис.4-9 в первом шаге первый работник вычислит – старшую цифру частного. Результат работы второго работника не нужен. Одновременно с записью цифры частного 0 третий работник запишет на место делимого сдвинутый на разряд влево новый остаток равный делимому. Получим новое делимое и .

Во втором шаге результат сравнения снова 0. Третий работник выполнит те же действия, что и в первом шаге. Получим сдвинутый влево новый остаток или очередное делимое и .

В третьем шаге цифра частного 1, так как . Разность . Заменив, старшие три разряда в сдвигаемом делимом на разность, третий работник запишет очередной сдвинутый остаток .

Процесс деления может продолжаться до бесконечности. Для прекращения процесса используют следующие правила:

• При делении целых с вычислением целого частного и остатка выполняют шагов. Искомый остаток имеет формат делителя и размещен в старших разрядах делимого вычисленного в последнем шаге. В примере рис.4-8a и рис.4-8б он выделен жирным шрифтом и равен 010. ¹³

• При делении целых и действительных чисел с вычислением частного в заданном формате с фиксированной точкой шаги выполняют до заполнения всех разрядов формата частного.

• При делении целых и действительных чисел с вычислением заданного количества значащих разрядов частного выполняют отсчет числа выполненных шагов, начиная с шага, результатом которого является первая единица в частном, и продолжают выполнять шаги до тех пор, пока количество отсчитанных шагов не станет равным заданному количеству значащих разрядов.

Операцию вычитания можно заменить сложением с дополнением . Например, в примере рис.4-9 дополнение 101 будет равно 011. Значения суммы будут использоваться только при и только ее младших разрядов, что позволит упростить выполнение операции сложения. Убедитесь, что от такой замены результат вычисления не изменится.

Можно вместо сложения с дополнением выполнять сложение с инверсией кода и при этом перенос в младший разряд задавать равным 1.

Существенно, что вычисление цифры частного выполняется за один шаг. Кроме того, всегда выполняется только одна операция (вычитание или сложение).