1. Умножение с преобразованием операндов в прямой код и произведения в дополнительный

Справедливость этой схемы вычислений очевидна. Остановимся лишь на некоторых особенностях и возможностях ее упрощения.

Применим правила вычисления произведения, описанные в разделе 4.4.2. Тогда задача сводится к вычислению значащих разрядов произведения, причем коды значащих разрядов операндов не равны 00…0.

Для вычисления младших разрядов прямого кода произведения операнды преобразуем в прямой код и перемножим их значащие разряды. Если знак произведения (–), заменим значащих разрядов произведения их дополнением для получения результата в дополнительном коде.

Пример 4-28. Выполняется умножение двоичных операндов в дополнительном коде варианта B с преобразованием операндов в прямой код и произведения в дополнительный.

В примере код 1|00…0_доп применяется для кодирования числа . Разряд знака и дополнительный старший разряд результата, выделенные жирным шрифтом, определены по отдельным правилам.

О братите внимание, что фактически перемножаются модули операндов X и Y.

П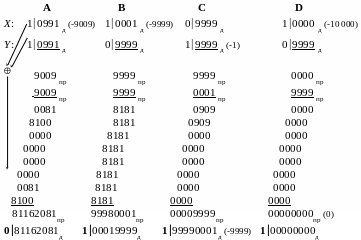 ример 4-29. Операнды представлены в дополнительном десятичном коде и код 1|00...0_доп не используется для представления числа . Поэтому старший дополнительный значащий разряд отсутствует, и при преобразовании в прямой код разрядность операндов не расширяется. Выполняется проверка операндов на 0. Поэтому знак произведения не равного 0 равен сумме по модулю 2 разрядов знака операндов.

Во всех вариантах примера вычислен прямой код значащих разрядов операндов, и матрицы частных произведений построены по тому же принципу, что и в примере 4-26 вариант D. Прямой код значащих разрядов произведения преобразован в дополнительный код с учетом знака произведения.

Вариант D демонстрирует, как будет вычислен ошибочный результат, если применить изложенные правила к кодам операндов 100...0 _доп.

Преобразование операндов в прямой код и результата в дополнительный требует затрат времени только при отрицательном значении преобразуемого кода. Если знак исходного кода (+), то результат преобразования уже известен. Так как длина кода произведения вдвое превышает длину операндов, то затраты на преобразование кода произведения примерно вдвое больше затрат на преобразование операнда, т.е. . Никогда не приходится выполнять преобразование двух операндов и результата, так как если оба операнда отрицательные, то произведение положительное.

В

Таблица 4.4

Знаки операндов X, Y и результата Z			Затраты времени на преобразование
X	Y	Z
+	+	+	0
+	–	–
–	+	–
–	–	+	2

табл.4.4 приведены суммарные затраты времени на преобразование операндов и результата при различных сочетаниях знаков операндов при условии, что отрицательные операнды преобразуются одновременно, а произведение после его вычисления.

Если принять, что знаки операндов независимые и равновероятные, то в среднем затраты времени на преобразования составят .

Преобразование операндов в прямой код можно частично совместить с вычислением суммы частных произведений. Для этого можно заменить значащие цифры отрицательных операндов обратными и выполнить умножение значащих разрядов. После замены цифр код значащих разрядов переменной равен , так как для получения значения к нему достаточно прибавить 1. Например, пусть . После замены значащих цифр обратными получим .

Умножение значащих цифр после преобразования операндов X и Y приведет к вычислению:

(4-04)

Чтобы получить прямой код значащих разрядов произведения т.е. , достаточно в процессе сложения строк матрицы частных произведений прибавить:

при (4-05)

при (4-06)

при (4-07)

П ример 4-30. Операнды в дополнительном двоичном коде и код 1|00...0_доп используется для представления числа . Разряды знака и дополнительный старший значащий разряд дополнительного кода произведения вычислены по отдельным правилам и показаны во всех вариантах примера жирным шрифтом.

В варианте A оба операнда отрицательные. Поэтому значащие цифры сомножителей заменены обратными. В матрицу частных произведений в соответствии с выражением (4-07) введены дополнительные слагаемые и 1, показанные жирным шрифтом. Так как знак произведения (+), то вычисленное произведение модулей операндов скопировано в соответствующие разряды результата.

В вариантах B и C один из операндов отрицательный. Его значащие цифры заменены обратными. В варианте B в соответствии с выражением (4-06) в матрицу частных произведений введено слагаемое , а в варианте C в соответствии с выражением (4-05) введено слагаемое . Так как знак произведения (–), то к разрядам знака и к дополнительному старшему разряду результата приписано дополнение произведения модулей операндов до веса старшего дополнительного разряда.

В варианте D оба операнда положительные. Поэтому замена цифр обратными не выполнялась и корректирующие поправки в матрице частных произведений равны 0.

Разумеется, что нулевые строки поправок в матрицу частных произведений можно не вводить, но это зависит от способа организации процесса вычислений.

Увеличение количества строк в матрице частных произведений усложняет вычисление их суммы. Можно сократить одну строку, если совместить частное произведение на младший разряд множителя со второй строкой корректирующих поправок в одну строку. Для этого в двоичной системе счисления совмещенную строку записывают по следующему правилу.

В совмещенную строку записывают:

• если 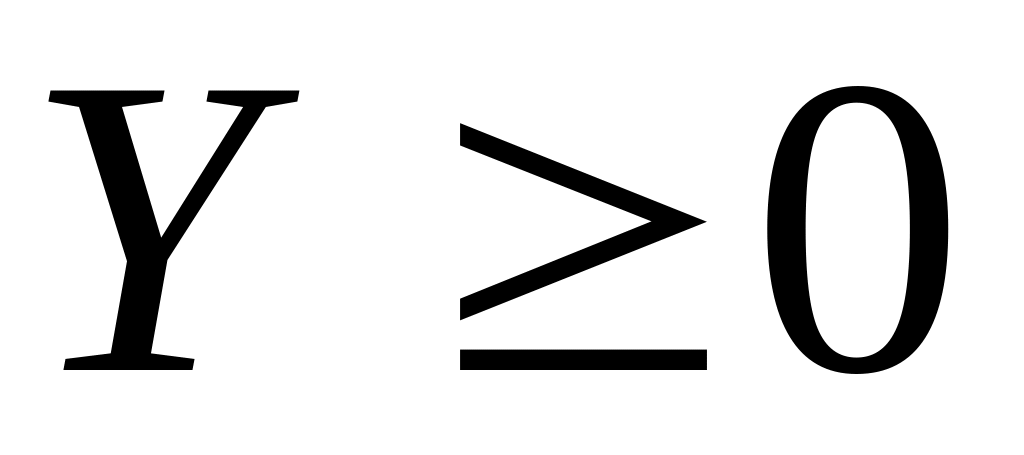, частное произведение на младший разряд Y;

• если и младший разряд равен 0, множимое, т.е. или ;

• если 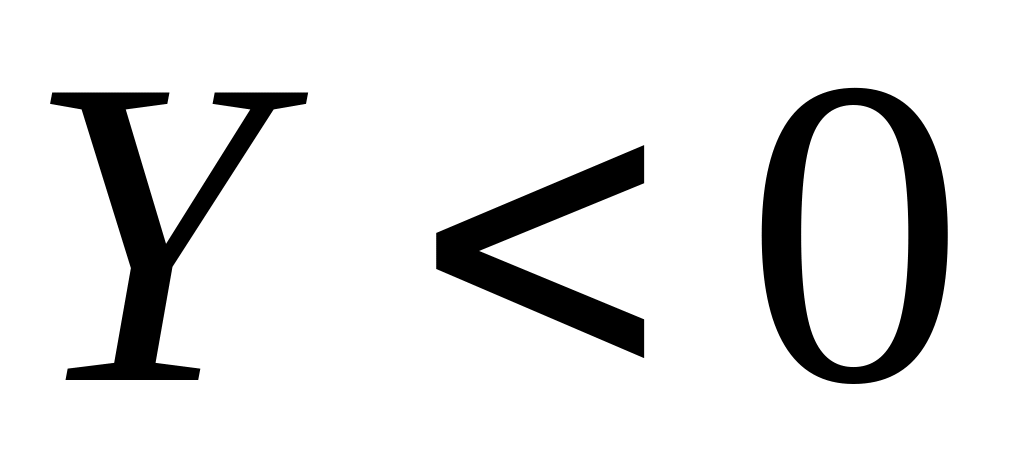и младший разряд равен 1, удвоенное множимое, т.е. сдвинутое на разряд влево с занесением 0 справа.

Действительно, совмещенная строка должна содержать сумму частного произведения на младший разряд множителя и корректирующей поправки второй строки. При (4-06) корректирующая поправка равна 0. Поэтому совмещенная строка должна содержать частное произведение на младший разряд множителя.

При (4-05), (4-07) и младшем разряде множителя равном 0 частное произведение равно 0, а корректирующая поправка в зависимости от знака X равна множимому или . Поэтому совмещенная строка должна содержать множимое.

При и младшем разряде множителя равном 1 частное произведение и корректирующая поправка равны множимому. Поэтому совмещенная строка должна содержать удвоенное множимое.

П ример 4-31. Операнды в дополнительном двоичном коде и код 1|00...0_доп используется для представления числа. Разряды знака и дополнительный старший значащий разряд дополнительного кода произведения вычислены по отдельным правилам. Вторая строка в матрицах частных произведений, показанная жирным шрифтом, совмещенная.

В вариантах A и С частное произведение на младший разряд множителя равно 0. Поэтому совмещенная строка содержит множимое.

В вариантах B и D частное произведение на младший разряд множителя и корректирующая поправка равны множимому. Поэтому совмещенная строка содержит удвоенное множимое, т.е. сдвинутое на разряд влево.

Рассмотренный способ умножения имеет самостоятельное значение в случае, когда операнды представлены в дополнительном двоичном коде, а результат необходимо получить в прямом коде.