1. Особенности сложения и вычитания в обратном коде

Результат выполнения операции в обратном коде равный нулю может быть (+0) или (–0). Знак нулевого результата зависит от значений операндов.

Результат сложения в обратном коде равен (+0) в единственном случае, когда оба операнда положительные нули: (+0) + (+0) = (+0).

Результат вычитания в обратном коде равен (–0) в единственном случае, когда из отрицательного нуля вычитается положительный ноль:

(–0) – (+0) = (–0).

Эти особенности выполнения операций в процессорах необходимо учитывать, чтобы исключить ошибки в результатах выполнения программ.

Пусть, например, необходимо изменить знак переменной x. Для этого можно воспользоваться операцией вычитания x из 0. Казалось бы, какая разница, из какого нуля вычитать x, из (+0) или из (-0). При в обоих случаях вычислим обратный код (-x).

Н апример,

При знак x изменится при вычитании x из (-0). При вычитании из (+0) случится ошибка (знак x не изменится).

Д

Займы: 00 00 11 11 00 00 00 00

0|000 (+0) 0|000 (+0) 1|111 (-0) 1|111 (-0)

x: - 0|000 (+0) - 1|111 (-0) - 0|000 (+0) - 1|111 (-0)

0|000 (+0) 0|001 1|111 (-0) 0|000 (+0)

- 1

Знак не изменился  0|000 (+0)

ействительно:

Если процессор заменяет вычитание сложением, используя отношение , и для этого изменяет знак обратного кода второго операнда, то ошибка случится только при вычитании (-0) из (-0), так как результат вычитания будет (-0).

Ошибка в определении знака может быть причиной грубейших ошибок в результатах выполнения программы. Например, при последующем делении на x результат вместо ( ) может стать равным ( ), а это далеко не одно и тоже. Или, если после ошибочного изменения знака необходимо вычислить . Разве и это одно и то же? В действительности , а .

При сложении (вычитании) в обратном коде в формате операндов обработчик прерывания по переполнению формата суммой (разностью) получит точный результат, приписав к полученному переполненному коду разряд знака инверсный цифре старшего разряда полученного кода. Кроме того, при P>2 обработчик должен заменить двоичный код цифры старшего значащего разряда кодом эквивалентным по значению и принятым для кодирования цифр в иных разрядах числа (см. раздел 4.3.1).

Если с целью вычисления или , где m – индекс младшего разряда, при выполнении операции сложения (вычитания), принять перенос (заем) в младший разряд операндов равным 1, количественный эквивалент суммы (разности) будет вычислен правильно при всех возможных сочетаниях операндов кроме при сложении, и при вычитании.

Д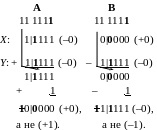 ействительно:

В вариантах A и B выполнено сложение и вычитание двоичных чисел в обратном коде с расширением формата операндов на один бит целого, показанный жирным шрифтом. При сложении перенос, а при вычитании заём, в младший разряд принят равным 1, показанной жирным шрифтом. Получены ошибочные результаты.

При прибавлении (вычитании) циклического переноса (займа) образуется новый перенос (заем) из знакового разряда (в примерах зачеркнут). Чтобы исключить ошибку необходимо зачеркнутый перенос (заем) считать циклическим и выполнять еще одно сложение (вычитание), что сильно осложняет вычисления. При любых иных сочетаниях значений операндов аналогичный перенос (заем) равен 0.

Предупреждение. При построении параллельного комбинационного сумматора (вычитателя) обратных кодов не следует соединять выход переноса (займа) из знакового разряда с входом переноса (займа) в младший разряд сумматора (вычитателя) для образования цепи циклического переноса (займа). В результате образуется многоранговая комбинационная схема, охваченная обратной связью. Эта схема неустойчивая и склонна к генерации. Неустойчивость вызвана задержками элементов схемы. Она проявляется, например, при сложении, когда коды операндов взаимно инверсные (их сумма должна быть равной нулю) и предшествовавшие операнды в одном из разрядов сформировали цепочку переносов равных 1. Новый набор операндов не препятствует распространению ранее сформированной и задержанной цепочке переносов распространяться по кольцу, что и приводит к генерации. Можно сказать, что в такой ситуации схема ”не знает”, какой 0 положительный или отрицательный она должна передать в результат.

Чтобы исключить неустойчивость схемы придется выполнять сложение посредством параллельного сумматора за два шага. В первом шаге вычисляется промежуточная сумма, а во втором – этот же сумматор прибавляет циклический перенос к промежуточной сумме.

Возможны иные решения. Например, параллельный сумматор передает промежуточную сумму со своего выхода схеме комбинационного счетчика, выполняющего учет значения циклического переноса.

Подобные решения усложняют аппаратуру сложения (вычитания) в обратном коде по сравнению со сложением (вычитанием) в дополнительном коде. Поэтому, несмотря на простоту преобразования прямого кода в обратный код и наоборот, и на простоту изменения знака числа в обратном коде, обратный код сравнительно редко применяют в устройствах вычислительной техники и автоматики.