Лабораторная работа №12

Моделирование динамических диссипативных систем

1. Моделирование нелинейной автоколебательной системы Ван дер Поля

Возможность существования периодического асимптотически устойчивого движения, изображаемого изолированной замкнутой траекторией в фазовом пространстве, к которой со временем притягиваются траектории из некоторой окрестности независимо от начальных условий, обеспечивается только в нелинейных диссипативных системах. Этот тип динамических систем называется автоколебательными системами. Математическим образом автоколебаний служит предельный цикл Пуанкаре – замкнутая изолированная траектория в фазовом пространстве, отвечающая периодическому движению.

В качестве примера динамической системы с предельным циклом Пуанкаре рассмотрим классический нелинейный осциллятор Ван дер Поля. Уравнение Ван дер Поля описывает простейший случай возникновения генерации в автоколебательной системе и имеет вид:

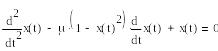
где – параметр системы характеризует подкачку энергии в систему от внешнего источника, и называется параметром возбуждения. Задает характер решения и начальные условия для и .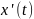

При положительных колебания в системе нарастают, но вследствие нелинейности системы их амплитуда ограничивается, а форма заметно отличается от синусоидальной. Система Ван дер Поля описывает сложный колебательный контур, характер диссипации в котором зависит от переменной .

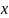Задание (1 вариант решения задачи):

1. пусть , а начальные условия , .

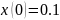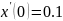2. уравнение Ван дер Поля решить с помощью блока Given…Odesolve.

3. получить фазовый портрет решения системы (рис. 1.1) и график колебаний (рис. 1.2)

Рис. 1.1. Фазовый портрет системы Ван дер Поля

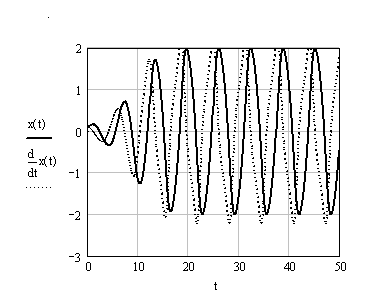
Рис. 1.2. Графики колебаний

Вывод: Положение равновесия в начале координат, в котором вблизи нуля можно пренебречь нелинейностью, является неустойчивым фокусом. Траектории из окрестности состояния равновесия асимптотически стремятся к предельному циклу. Как показывает анализ, предельный цикл является устойчивой изолированной структурой, притягивающей к себе траектории из любой точки на фазовой плоскости.

Таким образом, в динамических системах с нелинейной зависимостью диссипации энергии от переменной, совершающей колебания, впервые появляется принципиально новый тип устойчивого предельного множества фазовых траекторий – предельный цикл. На предельном цикле за время периода колебаний доли рассеиваемой и вносимой энергии строго компенсируются.

Развитием системы Ван дер Поля является система Ван дер Поля  Дуффинга, введенной по типу осциллятора Дуффинга. Эта модель учитывает возможность синхронизации автоколебательных систем импульсами.

Проанализируем систему Ван дер Поля – Дуффинга. Уравнение системы  дифференциальное уравнение второго порядка, которое можно разбить на два уравнения первого порядка:

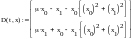
З адание (2 вариант решения задачи):

1. пусть , а вектор начальных условий:

2. систему нелинейных дифференциальных уравнений Ван дер Поля –Дуффинга решить с помощью функции rkfixed. Например,

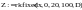
3. получить фазовый портрет решения системы (рис. 1.3) и график колебаний (рис. 1.4)

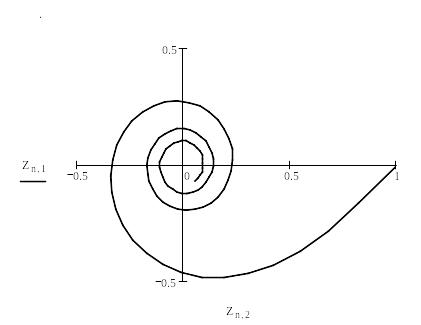
Рис. 1.3. Фазовый портрет системы Ван дер Поля – Дуффинга

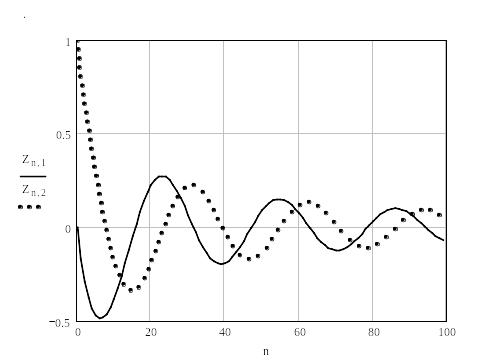
Рис. 1.4. График колебаний

Вывод: системы, колебания в которых возникают без внешних воздействий, называются автономными системами. К ним также относятся автогенераторы синусоидальных и релаксационных колебаний. Периодическая модуляция предельного цикла автономной системы приводит к тому, что фазовая траектория вращается вокруг предельного цикла и лежит на двумерной поверхности, представляющей собой поверхность тора. Эта поверхность будет устойчивым предельным множеством, к которому стягиваются со временем все траектории из некоторой окрестности тора (как изнутри него, так и снаружи). График колебаний показывает, что возникшие вначале колебания сразу же затухают во времени.