2.3 Уравнение сервопоршня
При выводе уравнения предполагается, что инерционные силы и силы трения малы по сравнению с силами давления. При принятых допущениях для описания динамики сервопоршня достаточно использовать уравнение, связывающее расход жидкости в подпоршневую полость и перемещение поршня:
,
(23)
где - плотность жидкости;
-площадь торца сервопоршня.
В безразмерных параметрах:
,
(24)
где
,
.
2.4 Уравнение дифференциального клапана
При выводе уравнения предполагается, что силы трения пренебрежимо малы по сравнению с силами давления жидкости и пружины.
С учетом принятых допущений уравнение баланса сил, действующих на поршень дифференциального клапана, имеет вид:
,
(25)
где
-сила,
обусловленная разностью давлений по
торцам поршня;
-сила
противодействия пружины;
-площадь торца поршня;
-жесткость
торца поршня;
-давление в полости под поршнем.
Подставляя
выражения для сил
и
в равенство (25) и выделяя составляющие
по отклонениям, можно получить:
,
в безразмерных параметрах:
,
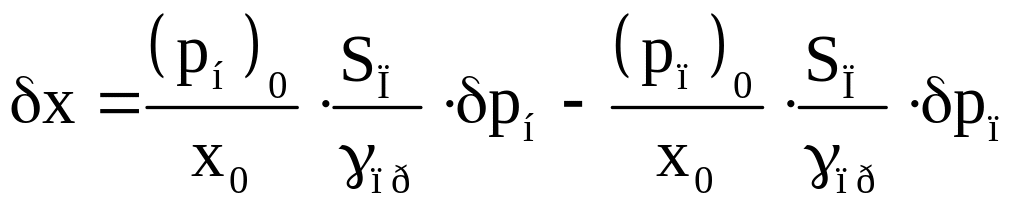(26)
где
,
,
.
Уравнение баланса расхода в подпоршневой полости записывается так:
,
(27)
где
-
расход жидкости, обусловленный движением
поршня;
- расход жидкости через жиклер;
- плотность жидкости;
- коэффициент расхода;
- площадь проходного сечения жиклера.
Уравнение (27) в отклонениях параметров перепишем в виде:
.
Принимая для отклонений расходов одно базовое значение , можно преобразовать последнее равенство к следующей безразмерной форме:
,
(28)
где , .
Для связи приращения расхода
с приращениями давлений в подпоршневой
полости
и за топливной форсункой
проводится линеаризация расходной
характеристики для
.
После линеаризации в безразмерных
параметрах получим:
.
(29)
Имея в виду,
что
,
можно выразить перемещение расхода,
обусловленного движением поршня, в
безразмерных параметрах:
.
(30)
Выражения (29) и (30) для приращений и подставляются в равенство (28), которое затем преобразовывается к виду:
.
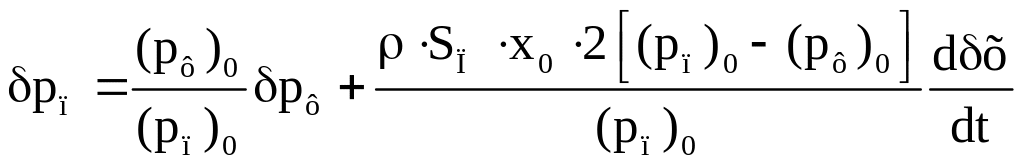(31)
Из совместного решения уравнений (26) и (31) можно получить уравнение дифференциального клапана:
,
(32)
где
;
;
.