2. Вывод дифференциального уравнения Уравнение дроссельного крана
При выводе дифференциальных уравнений звеньев за положительные направления координат принимаются такие, которые соответствуют направлениям, указанным в бланке задания.
При некотором установившемся режиме
верно равенство (если считать расход
через слив очень мал):
(закон
сохранения масс), где
- производительность насоса при
установившемся режиме;
- расход через дроссельный кран.
Производительность насоса можно
представить в виде:
,
где
- частота оборотов привода;
- параметр, от которого зависит угол
поворота наклонной шайбы.
Разложим
в ряд Тейлора, пренебрегая бесконечно
малыми членами второго порядка:
.
Если учесть, что мы рассматриваем малые отклонения параметров, то все зависимости можно считать линейными, а это значит:
,
где
- некоторые константы (коэффициенты
пропорциональности). Перепишем с учётом
этого ряд Тейлора:
.
Расход через дроссельный кран можно
представить в виде:
,
где
- перемещение дроссельного крана;
- давление, создаваемое насосом.
Разложим
в ряд Тейлора, пренебрегая бесконечно
малыми членами второго порядка:
.
Если учесть, что мы рассматриваем малые отклонения параметров, то все зависимости можно считать линейными, а это значит:
,
где
- некоторые константы (коэффициенты
пропорциональности). Перепишем с учётом
этого ряд Тейлора:
.
Запишем уравнение сохранения массы в
случае отклонения рабочих параметров:
;
;
;
;
;
;
,
где
- коэффициент усиления элемента по
воздействию
.
- коэффициент усиления элемента по
воздействию
.
- коэффициент усиления элемента по
воздействию
.
3. Построение структурной схемы и определение передаточных функций
Уравнения звеньев САР сведем в систему:
дроссельный кран;
чувствительный элемент;
сервопоршень.
Система уравнений содержит 6 переменных
(
),
т. е. за исключением управляющего
воздействия
и возмущающих воздействий
число переменных равно числу уравнений.
Систему дифференциальных уравнений
записываем в операторной форме:
Изобразим структурную схему дроссельного крана, описываемого уравнением:
Рисунок 3 – Структурная схема дроссельного крана.
Изобразим структурную схему чувствительного элемента, описываемого уравнением:
Предварительно
выразив для упрощения построения:
Рисунок 4 – Структурная схема чувствительного элемента.
Изобразим структурную схему сервопоршня, описываемого уравнением:
Предварительно выразим
для упрощения построения схемы:
Рисунок 5 – Структурная схема сервопоршня.
Изобразив схемы отдельных элементов системы, сгруппируем эти схемы. С помощью такой операции получим структурную схему САР. При группировке учтем, что у нас одно управляющее воздействие , и два возмущающих воздействия .
Рисунок 6 – Структурная схема САР.
Рисунок 7 – Структурная схема САР при возмущающем воздействии δx.
По структурной схеме легко прослеживается взаимодействие звеньев в системе регулирования давления топлива.
Для определения передаточной функции САР в разомкнутом состоянии в структурной схеме условно размыкается основная обратная связь и вводятся входной δpвх и выходной δpвых параметры разомкнутой системы. Тогда передаточная функция разомкнутой САР определяется как отношение:
При этом предполагается:
Выражение для
определяется как произведение:
где
В результате подстановки формул для
в выражение для
и
преобразований можно получить:
где
Передаточная функция замкнутой САР по
управляющему воздействию δpу,
определяется по формуле:
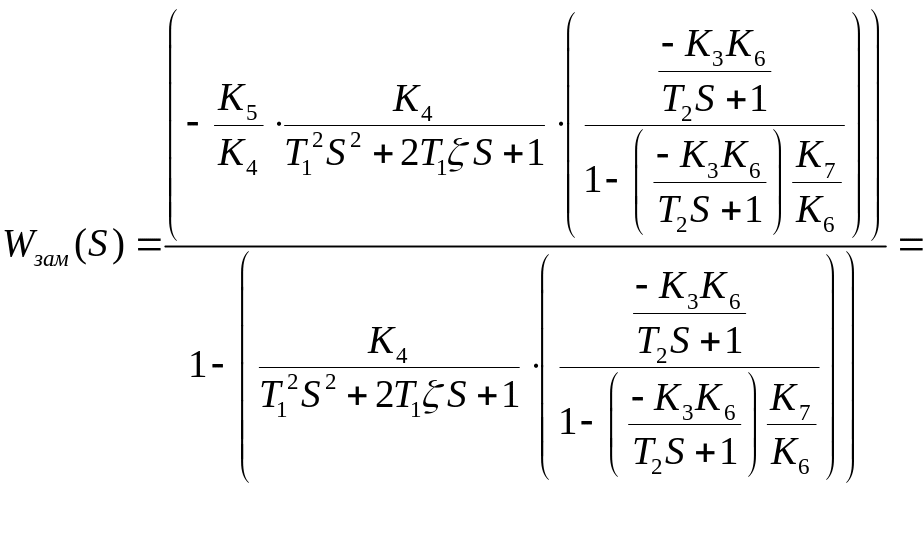
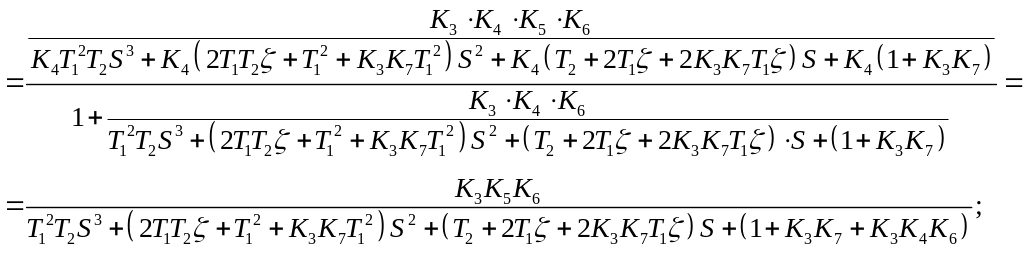
где
Собственные операторы замкнутой и разомкнутой САР имеют вид:
Передаточная функция замкнутой САР по
возмущающему воздействию
определяется по формуле:
.
Преобразуем это выражение:
;
;
,
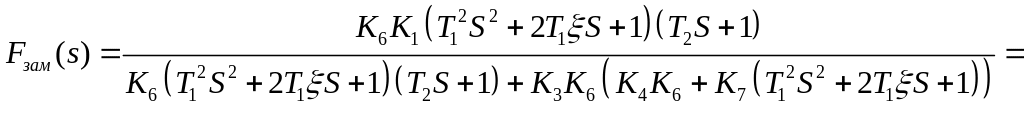
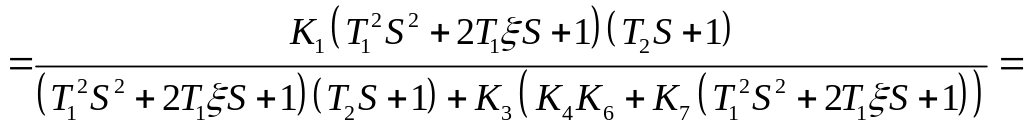где
.