
- •Образец титульного листа
- •1.Статика плоская произвольная система сил
- •Определение реакций опор составной конструкции
- •Определение реакций опор вала при действии пространственной произвольной системы сил
- •2.Кинематика Определение кинематических характеристик движения точки
- •2.Кинематика поступательного и вращательного движения твердого тела
- •3.Плоское движение твердого тела
- •4.Сложное движение точки
- •1. Определение . По теореме о сложении скоростей имеем .
2.Кинематика Определение кинематических характеристик движения точки
Задача 1.Заданы уравнения движения точки М:
![]()
где х,у- координаты движущейся точки, см.
Установить вид траектории точки и для момента времени t=1 с найти положение точки на траектории, её скорость, полное, касательное и нормальное ускорения, а также радиус кривизны траектории.
Решение.
1. Преобразуем параметрические уравнения движения точки:

Получено уравнение окружности с центром в точке с координатами х=-2 см; у = 3 см и радиусом R = 2 см. После определения траектории имеется возможность изобразить её в декартовой системе координат (рис. 11.16) и установить положение точки М момент времени t = 1 с:
![]()
Если положение точки окажется вне траектории, следует прекратить дальнейшие расчёты и найти ошибку в предыдущих расчётах.
2. Найдём проекции скорости на оси координат:

В момент времени t = 1 с Vx= -3,628 см/с; Vy = -2,094 см/с.
3.
Определим модуль скорости:
![]() В момент времени t=
lc
V=4,189
см/с. Покажем на рис. 11.16 в масштабе
составляющие скорости
В момент времени t=
lc
V=4,189
см/с. Покажем на рис. 11.16 в масштабе
составляющие скорости
![]() ,
,
![]() и
вектор скорости
и
вектор скорости
![]() ,
который
должен быть направлен по касательной
к траектории. Если это не произошло, в
расчётах допущена ошибка.
,
который
должен быть направлен по касательной
к траектории. Если это не произошло, в
расчётах допущена ошибка.
4.
Найдём проекции ускорения на оси
координат, учитывая, что
и
-
сложные функции:
![]()
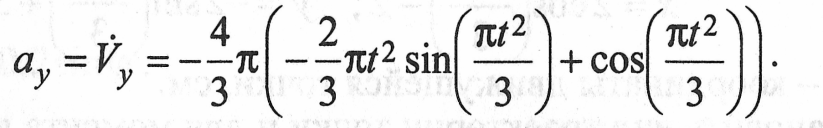
В момент времени t = 1 с ax= -8,014 см/с2; ay =- 5,503 см/с2.
5.
Определим модуль ускорения:
![]() В
момент времени t
= 1с
В
момент времени t
= 1с
а = 9,721 см/с2.
Покажем
на рис. 11.16 в масштабе составляющие
ускорения ах,
ау
и
вектор ускорения
![]() n,
который должен быть направлен в сторону
вогнутости траектории.
n,
который должен быть направлен в сторону
вогнутости траектории.
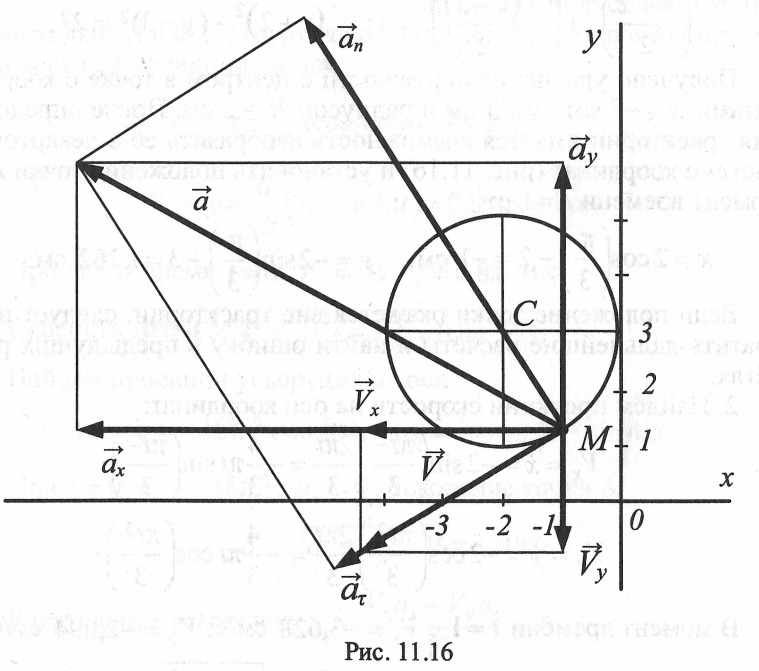
Вычислим касательное ускорение по формуле (11.28):
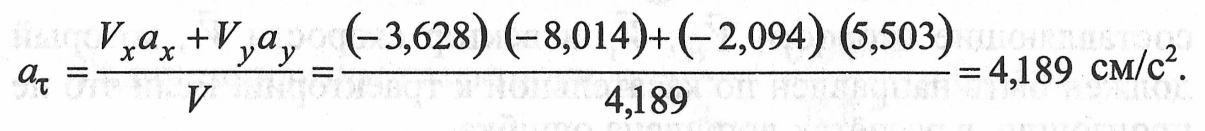
Положительный знак показывает, что движение точки М ускоренное, то есть направления векторов скорости и касательного ускорения совпадают.
Определим нормальное ускорение:
![]()
Покажем на рисунке векторы τ и n,.
8.Определим
радиус кривизны траектории:
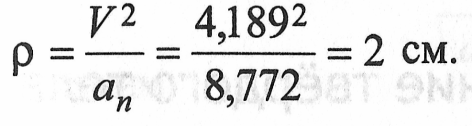
Для окружности радиус кривизны траектории совпадает с радиусом окружности: ρ= R = 2 см. Результаты расчётов сведём в табл. 11.1.
Таблица 11.1

2.Кинематика поступательного и вращательного движения твердого тела
Задача
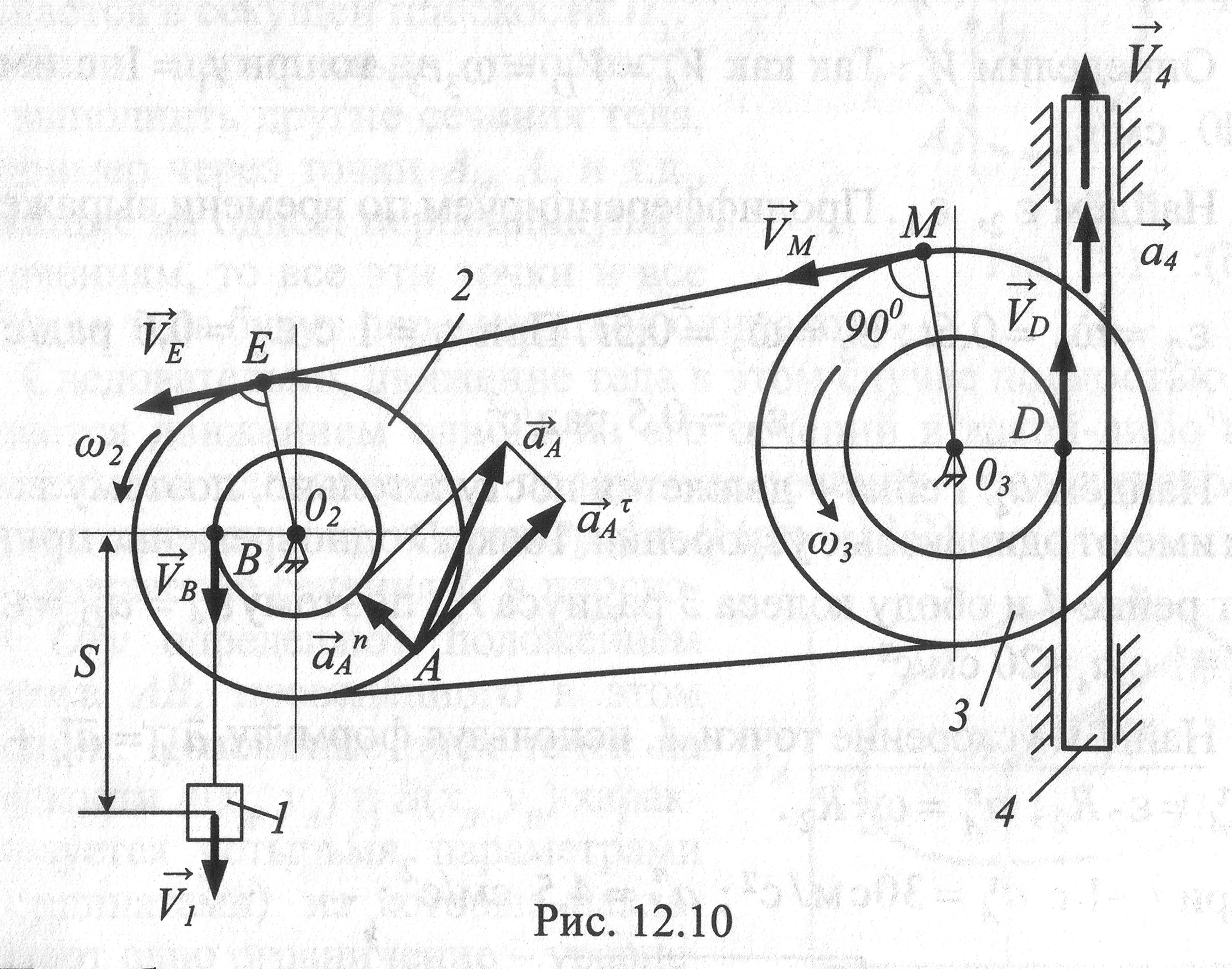
2. Груз
1
(рис.
12.10), опускаясь, согласно уравнению s
= 3
![]() +15,
где s
- расстояние груза от места схода нити
с поверхности вала в сантиметрах; t
- время
в секундах, приводит в движение колесо
2, ременную передачу, колесо 3 и рейку 4.
+15,
где s
- расстояние груза от места схода нити
с поверхности вала в сантиметрах; t
- время
в секундах, приводит в движение колесо
2, ременную передачу, колесо 3 и рейку 4.
Пренебрегая
скольжением ремня по ободам колес,
определить для момента времени
![]() =1
с скорость и ускорение рейки 4, угловые
скорости и ускорения колёс 2, 3 и ускорение
точки А,
если
=1
с скорость и ускорение рейки 4, угловые
скорости и ускорения колёс 2, 3 и ускорение
точки А,
если
![]() =30
см;
=30
см;
![]() =50
см - радиусы ступеней колеса 2;
=50
см - радиусы ступеней колеса 2;
![]() =40
см;
=40
см;
![]() =60
см -
радиусы
ступеней колеса 3.
=60
см -
радиусы
ступеней колеса 3.
Дано:
![]() ;
=30
см;
=50
см;
=60
см.
;
=30
см;
=50
см;
=60
см.
Определить:
![]() при
при
![]() с.
с.
Найдём
 ,
,
 .
Зная уравнение движения груза 1, определим
его скорость как функцию времени
.
Зная уравнение движения груза 1, определим
его скорость как функцию времени
 =
= =
9
=
9 .
Груз подвешен на нерастяжимом канате,
поэтому скорость груза 1 такая же, как
скорости точек на ободе колеса 2 радиуса
,
т.е.
.
Груз подвешен на нерастяжимом канате,
поэтому скорость груза 1 такая же, как
скорости точек на ободе колеса 2 радиуса
,
т.е.
 .
Найдем
как функцию времени:
.
Найдем
как функцию времени:
 .
(а)
.
(а)
Так
как колёса 2 и 3 связаны ременной передачей
(ремень нерастяжим), то
![]() ,
но
,
но
![]() ;
;
![]() .
.
![]() ,
,
поэтому
 . (б)
. (б)
При =1 с из (а) и (б) найдем = 0,3 рад/с; =-,25 рад/c.
Определим
 .
Так как
=
.
Так как
= ,
то при
=1
с имеем
=10
см/c.
,
то при
=1
с имеем
=10
см/c.Найдем
 .
Продифференцируем по времени выражения
(а), (б):
.
Продифференцируем по времени выражения
(а), (б):
![]() ;
;
![]() .
При
=1с
.
При
=1с
![]() =0,5
рад/
=0,5
рад/![]() .
.
Найдем
 .
Рейка 4 движется поступательно, поэтому
все её точки имеют одинаковые ускорения.
Точка D
одновременно принадлежит рейке 4 и
ободу колеса 3 радиуса
,
поэтому
.
Рейка 4 движется поступательно, поэтому
все её точки имеют одинаковые ускорения.
Точка D
одновременно принадлежит рейке 4 и
ободу колеса 3 радиуса
,
поэтому
 ;
при
=1с
и
=20
см/
;
при
=1с
и
=20
см/
Найдем ускорение точки А, используя формулу
 ;
; .
.
При
=1с
и
![]() =30
см/
;
=30
см/
;
![]() =4,5
см/
;
=4,5
см/
;
![]() см/
.
см/
.
