Questions
5.1 What kind will a matrix of double errors have? How will it change in comparison with a matrix of single errors (5.11)?
5.2 How are parameters of binary syndrome representation (see table 5.1) connected with general number of possible configurations variants which detected and corrected errors by syndrome decoding?
5.3 How will the syndrome format change if to apply a method of syndrome decoding to decoding double errors?
5.4 Give the generalized block diagram of syndrome decoder of a block (n, k) code. What is the function of syndrome analyzer?
Tasks
5.1 By the principles stated in the Example 5.1 represent structure a systematic block code intended for detection of double errors with the generating matrix (4.6).
5.2 The generator matrix of a code (7,4) is set:
.
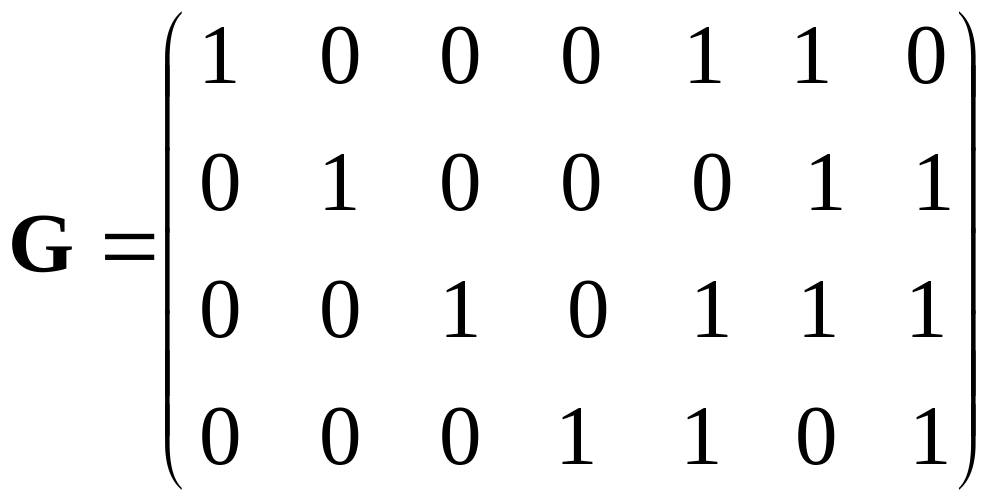Define allowed code word of this code b if the word of a primary code on a coder input a = (1110) is set.
5.3 Define code distance of a code (7, 4) with a generator matrix from the Task 5.2.
5.4 Represent a encoder structure of a code (7, 4) with the same generator matrix.
6 Boundaries of block codes parameters
The problem of the coding theory is the search of codes which at given block length n and rate Rcode provides a maximum of code distance dmin. Limits of these parameters are defined by the code boundaries.
6.1 Hamming upper bound
The
conclusion of the upper bound is based on reasons of spherical
packing (bound of spherical packing). At
given minimum distance between the allowed code words dmin.
The greatest rate can be reached, if the spheres surrounding each
word will be most densely packed. volume
of each sphere is equal
and
the number of spheres (number of code words) is equal 2k.
For best code the total quantity of spheres and number of all
possible words 2n should coincide.
Equality is reached for
densely packed
(perfect)
codes. area
of each code word represents sphere with radius (dmin
– 1)/2, and these areas of such codes not being crossed densely
fill with themselves all n-dimensional
space of code words. The inequality from here follows:
.
After simple transformations it is possible to receive obvious expression for rate of the perfect code:
. (6.1)
The dependence of Hamming upper bound is shown on figure 6.1 (curve «Hamming upper bound»). Hamming bound is fair both for linear and nonlinear codes.
6.2 Varshamov-Gilbert lower bound
For block codes it is possible to get the Varshamov-Gilbert lower bound which defines the possibility of codes existence with both parameters Rcode and dmin. The asymptotic form (for long codes) of this bound looks like:
Rcode 1 – H(dmin /n), (6.2)
where H (x) – binary entropy.
dependence of Varshamov-Gilbert lower bound for binary codes is shown on figure 6.1 (curve «Varshamov-Gilbert lower bound»). The bound guarantees existence of the codes which performances correspond to points arranged at least on a curve (or above it). Search of the codes ensuring the given minimum distance dmin and high enough rate Rcode at n→∞, ensuring at the same time a possibility of algorithms decoding realization with low complexity is one of important problem of the theory of coding.
