5.3 Majority decoding of block codes

Some block codes suppose realization of simple majority algorithm which is based on a possibility to express each information code symbol of a word by several ways through other received symbols. Let’s consider a systematic code (7,3):

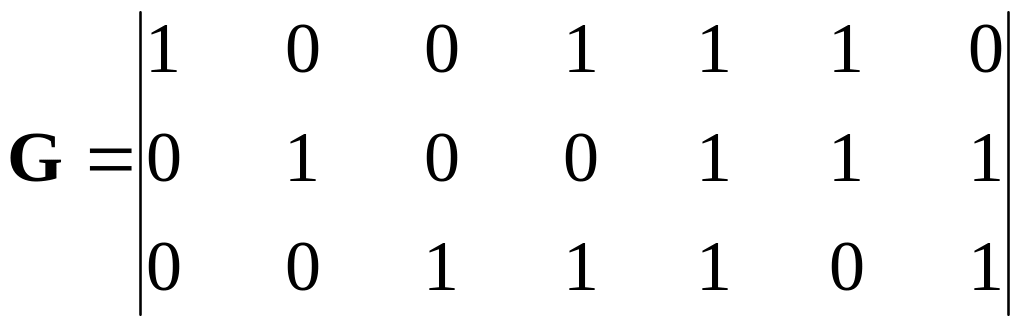. (5.13)

To this matrix corresponds transposed parity check matrix:

. (5.14)

Let's designate the received from the channel code word as

b = (b₁, b₂, b₃, b₄, b₅, b₆, b₇).

As considered code – systematic, first three symbols (b₁, b₂, b₃) are information symbols. Using structural properties of this code, it is possible to form during decoding both trivial and compound estimations of information symbols which are presented to table 5.2. On the basis of columns of parity check matrix (5.15) we will write down verifying parities:

b₁  b₃  b₄ = 0, b₁  b₂  b₃  b₅ = 0, b₁  b₂  b₆ = 0, b₂  b₃  b₇ = 0, (5.15)

which allow to form compound estimations. For example, on the basis of the first equality from (5.15) follows the compound estimation of the first information symbol b₁ = b₃  b₄. The trivial estimation of this symbol also is, actually, this symbol b₁ = b₁, as a code is systematic. Expressions for other information symbols are made similarly. They are presented in the table5.2.

Table 5.2 – Majority decoding of block code

Estimations of information symbols
Symbol b1	Symbol b2	Symbol b3
trivial
b1 = b1	b2 = b2	b3 = b3
compound
b1 = b3  b4 b1 = b5  b7 b1 = b2  b6	b2 = b4  b5 b2 = b6  b1 b2 = b3  b7	b3 =b5  b6 b3 =b7  b2 b3 =b4  b1

After formation of estimations they move on a majority element in which the decision on each information symbol is taken out on «the majority of voices».

For example, if estimations of information symbol b1 look like:

b₁ = b₁ = 1, b₁ = b₃  b₄ = 1, b₁ = b₅  b₇ =1, b₁ = b₂  b₆ = 0,

in which the quantity of estimations «1» exceeds quantity of estimations «0» the majority element passes the decision «on the majority»: b₁ = 1. The compound estimations enumerated in table 5.2 are called as orthogonal estimations as incoincident numerals enter into them. The number of orthogonal estimations N and a multiplicity of errors q_corr, corrected by majority decoding are in the ratio:

q_corr.  (N – 1)/2. (5.16)

The code with generator matrix (5.13) allows to form N = 3 orthogonal estimations and, accordingly, to correct unitary errors in information symbols by considerable simplification of decoding algorithm. It is necessary to notice that formation rules of estimations can have cyclic properties that simplifies decoding procedure.

Example 5.4 Structure of the majority decoder for the code (7, 3).

Let's generate structure of majority decoder of code (7, 3) on the basis of estimations system from table 5.2. It is easy to see, that checks have cyclic properties.

For example, indexes in compound estimations b₁ = b₃  b₄, b₂ = b₄  b₅ and b₃ =b₅  b₆ change on 1 towards increase. Taking it into account the decoder structure of code (7, 3) realizing majority decoding algorithm looks like shown on figure 5.3. The decoder consists of the shift register, the switchboard on the input, operated from system for block synchronization, schemes of estimations formation and the majority element. The decoder works as follows. At the beginning the switchboard on an input is established in position «1» and decoded code word b = (b₁, b₂, b₃, b₄, b₅, b₆, b₇) is entered in shift register cells. Thus on inputs of majority element the compound estimations defined by table 5.2 operate both trivial and compound estimations. The decision about transmitted information symbol b₁ is read out from an exit of majority element. Then the switchboard is established in position «2» and there is on one symbol shift of word. On this step, owing to cyclic properties of estimations the second information symbol are formed and the decision on an information symbol b₂ is read out from exit of majority element. Further process repeats up to reception on a output symbol b₃ etc.