6 Description of laboratory model
Laboratory work is executed on a computer in the HP VEE environment with using a virtual model, the block diagram of which is resulted on the figure 2. A model is intended for cyclic codes: (7, 4), (10, 5), (10, 6), (11, 7), (12, 8), (13, 9), (14, 10), (15, 11), encoding and decoding processes research.
A model allows research consistently encoding, transmission by a telecommunication channel and decoding. It contains the marked by a red color options which a student must set. The blue color windows are used for the model work results indication.
Coder forms the permitted code word by the r = n – k checking symbols calculation and add to them information symbols. The got code word is indicated on the encoder output.
For the transmission by a telecommunication channel implementation it is necessary to enter errors word, length п, consisting of 1 and 0. The symbol 1 is set in those positions, which an error at the transmission by a telecommunication channel must be in. In a telecommunication channel code word from encoder is added with combination of errors by XOR. The got code word is indicated on the telecommunication channel output.
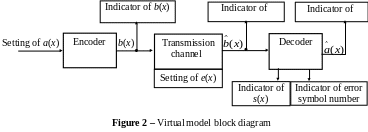
A decoder divides code word on his input, on a generate polynomial. A window under a decoder shows the code word syndrome (in binary presentation); a window left shows the decoder decision about the error symbol number (all codes researched in a model allow to correct single errors).
If a syndrome is zero, a decoder gives message "No errors". If a syndrome is not zero, on the syndromes table a decoder determines the error symbol number and "Error in хр " message, where р is error symbol number.
The syndromes table contains only п syndromes which correspond to п symbols of the decoded code word. The possible syndromes number is equal 2n – k. If n < 2n – k – 1, a syndrome which is absent in the syndromes table can appear in a decoder. In this case a decoder gives out the message "Unknown error".
If a decoder defined the error symbol number it gives out the message "Error in хр", it corrects this symbol and takes away n – k last symbols. If syndrome is zero or it is absent in the syndromes table, a decoder only takes away n – k last symbols. The information code word appear on the decoder output.
7 Requirements to the report
7.1 Title and objectives of laboratory work.
7.2 Results of the homework execution
7.3 Results of execution of items 5.2...5.5 of laboratory task.
7.4 Conclusions on every item of the laboratory task, with analysis of the got results (coincidence of experimental and theoretical information).
7.5 Signature of student about the laboratory work execution, teacher’s signature for the laboratory work defend with estimation and date.
Lw 4.3 Noise immunity of block error-control codes researching
1 Objectives
1.1 Study of block diagram of (n, k) block error-control codes decoder with the errors correction.
1.2 Experimental researches of noise immunity of (n, k) block error-control codes with the errors correction.
1.3 Calculations of coding gain (CG) from data of experimental researches of noise immunity of (n, k) block error-control codes.