3.3.4.6. Оценка точности результатов угловых и линейных измерений
Перед
уравниванием всей системы полигонометрических
ходов на объекте необходимо оценить
реальную точность измерений углов и
сторон в ходах. Правильно подсчитанные
СКО измерения углов и сторон
позволяют правильно назначить веса
угловых и линейных измерений и,
следовательно, обеспечить оптимальные
условия для уравнивания отдельных ходов
и систем ходов.
Оценка точности измерения углов может выполняться:
по уклонениям от среднего в приёмах;
по разностям двойных измерений;
по значениям угловых невязок в отдельных полигонометрических ходах.
Соответственно
есть и три разных набора формул для
вычисления СКО измерения углов
.
Для
одного приёма измерения угла
,
где
-
количество приёмов,
-
уклонение угла в каждом приёме от
среднего из всех приёмов. На пункте
число приёмов бывает от 2 до 6, поэтому
надёжность такого подсчёта
невелика, тем более, что на разных пунктах
значение
может получиться разным. При использовании
результатов измерений на
пунктах хода СКО измерения угла одним
приёмом вычисляют по формуле
,
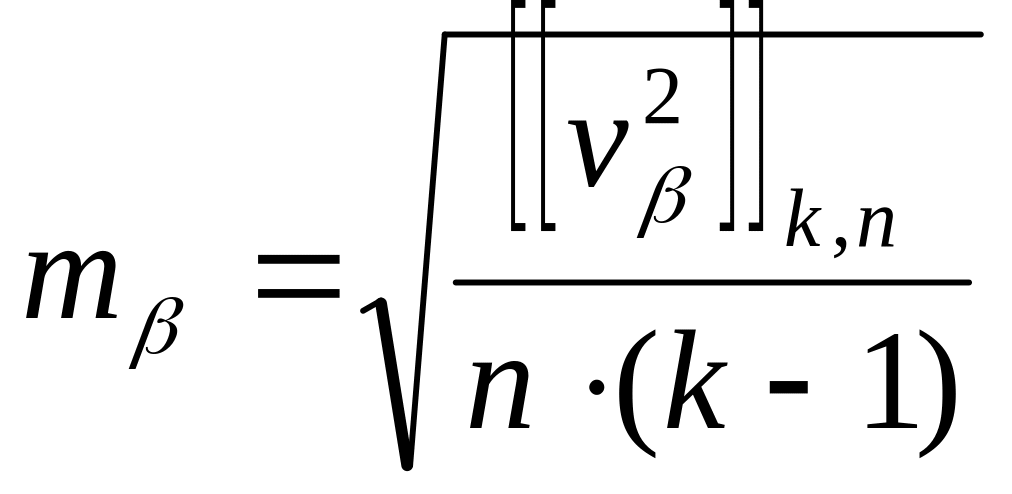а СКО среднего значения угла из приёмов – по формуле
.
Набор формул для оценки точности измерения углов по разностям двойных измерений мы приводить не будем.
СКО измерений углов по значениям невязок в отдельных ходах (полигонах) вычисляется по формуле
;
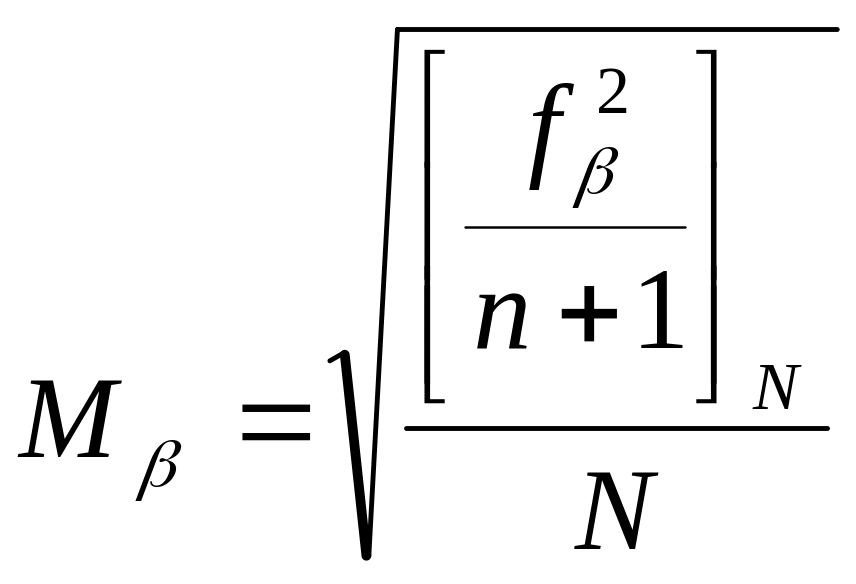здесь:
-
угловая невязка в ходе,
-
количество сторон в ходе,
-
количество ходов (полигонов).
3.3.5. Уравнивание полигонометрического хода коррелатным способом мнк
В
полигонометрическом ходе, как и в любом
построении, выделяют три типа данных:
исходные данные (это – координаты
первого и последнего пунктов хода и
дирекционные углы примычных направлений
в начале и в конце хода); измеренные
данные (это – горизонтальные углы, их
количество равно
,
и длины сторон хода, их количество равно
);
определяемые данные (это – координаты
определяемых пунктов, их количество
равно
).
Метод наименьших квадратов имеет две модификации: параметрический и коррелатный способы уравнивания. В первом из них количество нормальных уравнений равно количеству определяемых неизвестных, во втором – количеству избыточных измерений; при ручном счёте тот или иной способ выбирали в зависимости от соотношения этих чисел; уравнивание полигонометрического хода, как правило, выполнялось коррелатным способом. При машинной обработке на персональном компьютере количество нормальных уравнений большого значения не имеет, и на первый план выступает простота алгоритма того или иного способа. По этому показателю параметрический способ уравнивания оказался предпочтительнее коррелатного, и в настоящее время большинство программ уравнивания геодезических построений составлены в соответствии с алгоритмом параметрического уравнивания. Коррелатный способ мы рассматриваем в историческом и теоретическом аспектах проблемы уравнивания.
Как отмечалось в главе 2, в матричной записи теория коррелатного способа МНК-уравнивания имеет следующий вид. Система уравнений поправок записывается в виде матричного уравнения
;
здесь
-
матрица коэффициентов уравнений поправок
размером
(
строк и
столбцов);
-
вектор поправок размером
(
строк,
1 столбец);
-вектор
невязок размером
(
строк,
1 столбец);
-
количество измерений,
-
количество определяемых неизвестных,
-
количество избыточных измерений, равное
количеству условий
.
Условие
минимума суммы квадратов поправок
записывается так
.
Система нормальных уравнений коррелат имеет вид
,
где
-
матрица коэффициентов нормальных
уравнений коррелат,
;
-
матрица обратных весов измеренных
элементов,
;
-
вектор коррелат размером
.
Поправки в измерения выражаются через
коррелаты по формуле
.
В отдельном полигонометрическом ходе три избыточных измерения и три условных уравнения связи.
Первое уравнение – условное уравнение дирекционных углов
,
где
-
угловая невязка хода; для левых углов
;
-
количество сторон в ходе;
-
поправки в измеренные значения углов.
Ещё два уравнения – это условные уравнения координат (X и Y):
;
.
Здесь
и
-
координатные невязки;
,
.
Поправки
и
- это поправки к вычисленным значениям
приращений координат, которые являются
зависимыми величинами; по теории МНК в
уравнениях должны стоять поправки к
измеренным элементам
и
.
Преобразование условных уравнений
координат выполняется с помощью
дифференциальных формул приращений
координат
;
.
В
этих формулах через
и
обозначены приращения координат по
сторонам хода;
и
- поправки в дирекционные углы и длины
сторон хода. Если выразить
в километрах, поправки в углы – в
секундах, поправки в длины сторон – в
сантиметрах, то значение
.
Условные уравнения координат запишутся в виде
,
.
Эти уравнения ещё не являются окончательными, так как поправки в дирекционные углы нужно выразить через поправки в измеренные углы. Выразив каждый дирекционный угол через измеренные углы, получим
,
.
Таким образом, все условные уравнения получены.
Нормальные уравнения коррелат имеют вид
,
,
.
В
этих уравнениях через
обозначен обратный вес измеренных
величин
.
Приведём полную запись нормальных уравнений коррелат:
,
Из
решения нормальных уравнений коррелат
находят значения трёх коррелат
.
Поправки в измеренные значения углов и сторон хода вычисляют по формулам
,
.
Поправки
в дирекционные углы получают по поправкам
.
Уравненные
углы, дирекционные углы и длины сторон
находят путём введения поправок
.
Уравненные значения приращений координат
находят по уравненным длинам и дирекционным
углам сторон хода. Заключительным
контролем вычислений являются равенства
,
.