
- •2 Станция
- •2.2. Влияние кривизны Земли и вертикальной рефракции на измеряемое превышение
- •2.3.2.3. Исследование правильности хода фокусирующей линзы.
- •2.3.2.4. Определение диапазона и ошибки работы компенсатора.
- •2.4. Устройство, поверки и исследования нивелирных реек
- •2.5. Нивелирование III класcа
- •2.6.2. Обработка нивелирной сети с одной узловой точкой
- •2.6.3. Обработка нивелирной сети по способу эквивалентной замены
- •2.6.4. Обработка нивелирной сети по способу узлов
- •2.6.5. Обработка нивелирной сети по способу полигонов
- •2.6.6. Обработка нивелирной сети параметрическим способом мнк
- •2.7. Проектирование нивелирования III класса
- •2.9. Поиск грубых ошибок измерений в нивелирных сетях
- •После умножения выражения (2.4) слева на матрицу p получим
2.6.6. Обработка нивелирной сети параметрическим способом мнк
В параметрическом способе МНК-уравнения приняты следующие обозначения:
- измеренные величины (превышения) с весами соответственно ; количество измеренных превышений равно ;
![]() -
уравненные значения превышений;
-
уравненные значения превышений;
![]() -
поправки из уравнивания к измеренным
превышениям; связь уравненных превышений,
поправок в измерения и измеренных
превышений выражается формулой
-
поправки из уравнивания к измеренным
превышениям; связь уравненных превышений,
поправок в измерения и измеренных
превышений выражается формулой
![]() ;
;
![]() -
определяемые неизвестные (отметки
реперов); их количество равно
,
причём
-
определяемые неизвестные (отметки
реперов); их количество равно
,
причём
![]() .
.
Далее
выражают уравненные значения превышений
в виде функций от определяемых неизвестных
![]() и вводят понятие приближённые значения
определяемых неизвестных
и вводят понятие приближённые значения
определяемых неизвестных
![]() ;
приближённые значения неизвестных
можно либо вычислить каким-либо способом,
либо принять произвольными, но так,
чтобы отличие приближённых и уравненных
значений неизвестных различались на
малые величины
;
приближённые значения неизвестных
можно либо вычислить каким-либо способом,
либо принять произвольными, но так,
чтобы отличие приближённых и уравненных
значений неизвестных различались на
малые величины
![]() .
Значения неизвестных представляют в
виде суммы
.
Значения неизвестных представляют в
виде суммы
![]() и раскладывают функции
и раскладывают функции
![]() в ряд Тейлора относительно поправок
,
ограничиваясь членами первого порядка
малости. Полученные таким образом
уравнения называются параметрическим
уравнениями поправок
в ряд Тейлора относительно поправок
,
ограничиваясь членами первого порядка
малости. Полученные таким образом
уравнения называются параметрическим
уравнениями поправок
![]() .
.
В
этой формуле буквами
![]() обозначены частные производные функции
по определяемым неизвестным
.
Свободный член
получается по формуле
обозначены частные производные функции
по определяемым неизвестным
.
Свободный член
получается по формуле
![]() .
Функция
.
Функция
![]() представляется
в виде
представляется
в виде
![]() ,
,
и для выполнения условия минимума функции приравнивают нулю её частных производных по .
На
следующем этапе составляют
нормальных уравнений с
параметрами – поправками к приближённым
значениям неизвестных. Из решения
системы нормальных уравнений (по схеме
Гаусса, методом квадратных корней или
путём обращения матрицы коэффициентов)
находят поправки
к приближённым значениям неизвестных.
Далее вычисляют уравненные значения
неизвестных
![]() ,
поправки в измерения, уравненные значения
измеренных элементов и выполняют оценку
точности. При оценке точности вычисляют
ошибку единицы веса
,
поправки в измерения, уравненные значения
измеренных элементов и выполняют оценку
точности. При оценке точности вычисляют
ошибку единицы веса
![]()
и
сравнивают её с проектным значением
ошибки единицы веса
;
затем для любого параметра геодезического
построения вычисляют вес
![]() и среднюю квадратическую ошибку
уравненного значения этого параметра
и среднюю квадратическую ошибку
уравненного значения этого параметра
![]() .
.
В нивелирных сетях значения всех частных производных измерений равны либо плюс единице, либо минус единице, либо нулю, так как превышение по линии равно разности отметок реперов в конце линии и в её начале
![]() ;
;
если один из реперов – начальный или конечный, - является исходным, то частная производная по его отметке равна нулю. Уравнения поправок содержат в левой части всего два члена (или один член) с неизвестными поправками в отметки реперов. Приближённые значения отметок вычисляют обычно по измеренным превышениям, начиная от исходных реперов, поэтому часть свободных членов параметрических уравнений поправок будут равны нулю.
В матричной записи параметрический способ МНК-уравнивания имеет вид
-
параметрические уравнения поправок
![]() ;
;
нормальные уравнения параметров-поправок
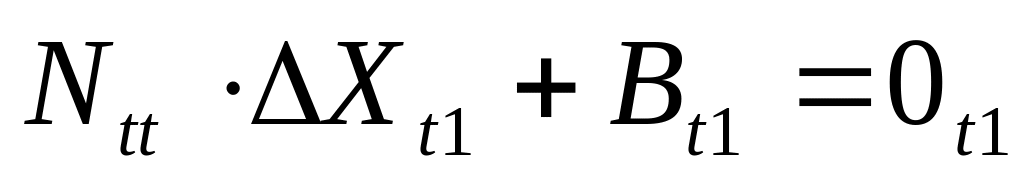 ;
;матрица коэффициентов нормальных уравнений
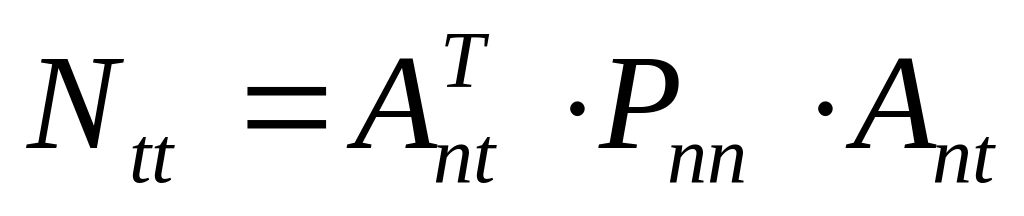 ;
;вектор свободных членов нормальных уравнений
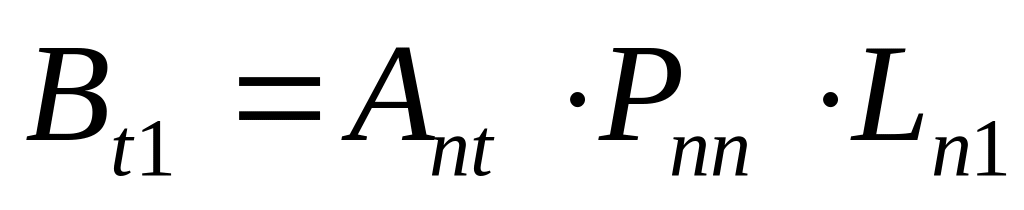 ;
;вектор поправок к приближённым значениям неизвестных
 .
.
В этих формулах:
![]() -
вектор свободных членов параметрических
уравнений поправок,
-
вектор свободных членов параметрических
уравнений поправок,
![]() ;
;
![]() -
диагональная матрица весов измерений;
-
диагональная матрица весов измерений;
![]() -
матрица коэффициентов параметрических
уравнений поправок размером
строк и
столбцов.
-
матрица коэффициентов параметрических
уравнений поправок размером
строк и
столбцов.
- вектор поправок в результаты измерений.
