2.6.2. Обработка нивелирной сети с одной узловой точкой

В связи с широким внедрением компьютеров в практику геодезических вычислений исчезла актуальность "ручных" способов обработки сложных нивелирных сетей, и в настоящее время обработка нивелирных сетей выполняется на ПК по программам, в которых реализованы алгоритмы строгого МНК-уравнивания.

Из применяемых в прежние времена "ручных" способов: - способ эквивалентной замены, способ узлов, способ полигонов, - особый теоретический интерес представляет первый способ, в котором путем несложных вычислений нивелирная сеть с несколькими узловыми точками может быть преобразована в сеть с одной узловой точкой. В способе узлов и способе полигонов уравнивание выполняется методом приближений; оба они были разработаны русским учёным геодезистом В.В. Поповым.

Пусть в репере 1 сходятся n ходов; длины ходов обозначим через , измеренные превышения по ним - через (рис.18). Отметку репера 1 можно получить раз (на рис.18 ):

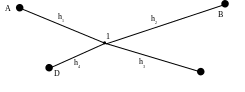
C

Рисунок 18 – Схема нивелирной сети с одной узловой точкой

- из 1-го хода,

  - из 2-го хода,

- из 3-го хода,

- из 4-го хода.

При разной длине ходов ошибки превышений по ходам также различны, следовательно, отметки  будут получены с разными весами, и для вычисления средней отметки репера 1 нужно применить формулу весового среднего

,

где - вес i-того хода; ( - константа).

После вычисления сеть разделяется на четыре изолированных одиночных хода, каждый из которых обрабатывается по известной методике.

2.6.3. Обработка нивелирной сети по способу эквивалентной замены

Идея способа эквивалентной замены заключается в том, что два нивелирных хода, сходящихся в одной точке, можно заменить одним эквивалентным ходом, вес которого равен сумме весов составляющих его двух ходов, и превышение по которому равно средне-весовому из превышений двух ходов. Рассмотрим нивелирную сеть, изображенную на рис.19.

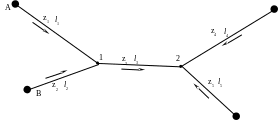
C

D

Рисунок 19 – Схема нивелирной сети

Сначала заменим ходы 1 и 2 одним эквивалентным ходом , вес которого равен

.

Длину хода выразим через длины ходов 1 и 2

.

Отметка репера 1, вычисленная по превышениям ходов 1 и 2 или из эквивалентного хода , будет равна

После первой замены вид сети изменится (рис.20).

C

z₄

l₄

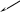
K

1

2

z₁₂

z₃

l_z12

l₃

z₅

l₅

D

Рисунок 20 – Вид нивелирной сети после первой замены

Следующим шагом будет "сложение" хода с ходом 3; эквивалентный им ход обозначим ; его длина будет

.

Отметка репера 2, полученная из ходов 1, 2, 3 или из эквивалентного хода   , будет равна

.

Вес отметки репера 2, полученной из эквивалентного хода , будет равен

.

Вид нивелирной сети после второй эквивалентной замены изображён на рис.21.

C

z₄

l₄

z₁₂₃

l_z123

K

2

z₅

l₅

D

Рисунок 21 – Схема нивелирной сети после второй замены

В узловой точке - репере 2, - сходятся три хода, и дальнейшая обработка сети выполняется по методике обработки нивелирной сети с одной узловой точкой, описанной выше, то есть,

, , , , .

.

Поправки в измеренные превышения получают по следующим формулам

; ; ;

; ; ; .

Оценка точности уравненной нивелирной сети заключается в вычислении средней квадратической ошибки единицы веса , средней квадратической ошибки превышения на один километр хода  и ошибок отметок реперов

,

,

.

В этих формулах: - вес i-того хода; - поправка из уравнивания в превышение по i-тому ходу; - количество ходов в сети (количество измеренных превышений); - количество определяемых реперов в сети; - константа при вычислении весов, как правило ; - длина i-того хода; - вес репера 2.

Чтобы получить вес репера 1, нужно уравнять сеть заново, заменяя ходы 4 и 5 эквивалентным ходом и затем “складывая” ход 3 и полученный эквивалентный ход. В результате таких замен узловым репером, в котором будут сходиться три хода, должен стать репер 1.

Для нивелирных сетей сложной формы разработаны методики эквивалентной замены “звезда - треугольник”, “треугольник - звезда” и другие. Как отмечается в литературе, такие замены интересны прежде всего с теоретической точки зрения, а практически они очень громоздки и неудобны, а потому способ эквивалентной замены рекомендуется применять для обработки или предрасчёта точности небольших по размерам и относительно простых по форме нивелирных сетей.