Графическое представление равноускоренного прямолинейного движения

График скорости

Для построения этого графика на оси абсцисс откладывают время движения, а на оси ординат - скорость (проекцию скорости) тела. В равноускоренном движении скорость тела с течением времени изменяется. Если тело движется вдоль оси О_х, зависимость его скорости от времени выражается формулами v_x=v_0x+a_xt и v_x=at (при v_0x = 0).

И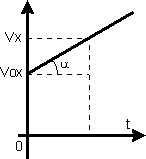 з этих формул видно, что зависимость v_х от t линейная, следовательно, графиком скорости является прямая линия. Если тело движется с некоторой начальной скоростью, эта прямая пересекает ось ординат в точке v_0x. Если же начальная скорость тела равна нулю, график скорости проходит через начало координат.

Г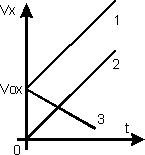 рафики скорости прямолинейного равноускоренного движения изображены на рис. 9. На этом рисунке графики 1 и 2 соответствуют движению с положительной проекцией ускорения на ось О_х (скорость увеличивается), а график 3 соответствует движению с отрицательной проекцией ускорения (скорость уменьшается). График 2 соответствует движению без начальной скорости, а графики 1 и 3 - движению с начальной скоростью v_ox. Угол наклона a графика к оси абсцисс зависит от ускорения движения тела. Как видно из рис. 10 и формулы (1.10),

tg=(v_x-v_0x)/t=a_x.

П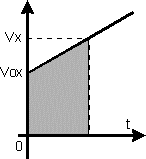 о графикам скорости можно определить путь, пройденный телом за промежуток времени t. Для этого определим площадь трапеции и треугольника, закрашенных на рис. 11.

В выбранном масштабе одно основание трапеции численно равно модулю проекции начальной скорости v_0x тела, а другое ее основание - модулю прокции его скорости v_х в момент времени t. Высота трапеции численно равна длительности промежутка времени t. Площадь трапеции

S=(v_0x+v_x)/2t.

Использовав формулу (1.11), после преобразований находим, что площадь трапеции

S=v_0xt+at²/2.

Правая часть последнего равенства представляет собой выражение, определяющее путь, пройденный телом. Следовательно, путь, пройденный в прямолинейном равноускоренном движении с начальной скоростью, численно равен площади трапеции, ограниченной графиком скорости, осями координат и ординатой, соответствующей значению скорости тела в момент времени t.

В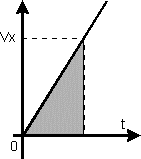 выбранном масштабе высота треугольника (рис. 11,б) численно равна модулю проекции скорости v_х тела в момент времени t, а основание треугольника численно равно длительности промежутка времени t. Площадь треугольника S=v_xt/2.

Использовав формулу 1.12, после преобразований находим, что площадь треугольника

S= at²/2.

Правая часть последнего равенства представляет собой выражение, определяющее путь, пройденный телом. Следовательно, путь, пройденный в прямолинейном равноускоренном движении без начальной скорости, численно равен площади треугольника, ограниченного графиком скорости, осью абсцисс и ординатой, соответствующей скорости тела в момент времени t.

График зависимости координаты от времени (график движения)

Для построения этого графика на оси абсцисс откладывают время движения, а на оси ординат - координату движущегося тела.

Пусть тело движется равноускоренно в положительном направлении О_х выбранной системы координат. Тогда уравнение движения тела имеет вид (1.16):

x=x₀+v_0x·t+a_xt²/2.

Выражению (1.16) соответствует известная из курса математики функциональная зависимость у=ах²+bх+с (квадратный трехчлен). В рассматриваемом нами случае a=|a_x|/2, b=|v_0x|, c=|x₀|.

Как известно, графиком этой зависимости является парабола, ветви которой направлены вверх, если a>0, или вниз, если а<0.

Вершина этой параболы находится в точке, абсцисса которой х=-b/2a, а ордината у=c-b²/4a. В рассматриваемом нами случае

x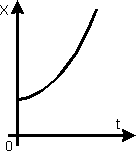 =-|v_0x|/|a_x|, y=|x₀|-|v₀x₂|/2|a_x|.

Как видно из этих формул, при движении тела без начальной скорости (v_0x=0) вершина этой параболы находится в точке х= x₀. График зависимости от времени координаты тела, движущегося равноускоренно без начальной скорости в положительном направлении оси О_х, изображен на рис. 12.

График пути

Для того чтобы построить этот график, на оси абсцисс откладывают время, а на оси ординат - длину пути, пройденного телом. В равноускоренном прямолинейном движении зависимость пути от времени выражается формулами

s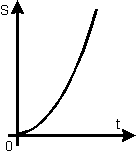 =v₀t+at²/2, s= at²/2 (при v₀=0).

Как видно из данных формул, эта зависимость квадратичная. Из обеих формул следует также, что s = 0 при t = 0. Следовательно, графиком пути прямолинейного равноускоренного движения является ветвь параболы. На рис. 13 показан график пути при v₀ =0.