
- •Завдання для розрахунково-графічної роботи
- •11) Жодне с не є d. Всі а є d. Всі в є с. Отже, всі в не є а.
- •13) Деякі с не є d. Всі а є не d. Всі в є с. Отже, всі в є а.
- •15) Деякі с не є d. Всі а є d. Всі в є не с. Отже, всі в є а.
- •11)├ , Якщо х не вільна в в.
- •12)├ , Якщо х не вільна в в.
- •22)├ , Якщо х не вільна в в.
- •V. Довести примітивну рекурсивність функцій:
- •VI. Знайти результат застосування машини Тьюрінга з програмою р до
- •VII. Побудувати нормальний алгоритм Маркова для перетворення
Завдання для розрахунково-графічної роботи
(2 семестр)
І. Звести формули А та В до випередженої нормальної форми,
записати сколемівську форму:
1)
![]() ;
;
![]() .
.
2)
![]() ;
;
![]() .
.
3)
![]() ;
;
![]() .
.
4)
![]() ;
;
![]() .
.
5)
![]() ;
;
![]() .
.
6)
![]() ;
;
![]() .
.
7)
![]() ;
;
![]() .
.
8)
![]() ;
;
![]() .
.
9)
![]() ;
.
;
.
10)
;
![]() .
.
11)
![]() ;
;
![]() .
.
12)![]() ;
;
![]() .
.
13)![]() ;
;![]() .
.
14)
![]() ;
;
![]() .
.
15)
![]() ;
;
![]() .
.
16)
![]() ;
;
![]() .
.
17)
![]() ;
;
![]() .
.
18)
![]() ;
;
![]() .
.
19)
![]() ;
;
![]() .
.
20)
![]() ;
;
![]() .
.
21)
![]() ;
;
![]() .
.
22)
![]() ;
;
![]() .
.
23)
![]() ;
;
![]() .
.
24)
![]() ;
;
![]() .
.
ІІ. Записати речення у вигляді формули логіки предикатів. Методом резолюцій встановити, чи буде висновок логічним наслідком гіпотез. Результат зобразити за допомогою діаграм Ейлера-Венна:
1) Жодне С не є D. Всі А є D. Всі В є С. Отже, всі В не є А.
2) Всі С не є D. Всі А не є D. Всі В є С. Отже, всі В є А.
3) Деякі С не є D. Всі А є не D. Всі В є С. Отже, всі В є А.
4) Всі А не є В. Деякі В є С. Отже, не існує А, таких що В або С.
5) Деякі С не є D. Всі А є D. Всі В є не С. Отже, всі В є А.
6) Жодне С не є D. Всі А є не D. Деякі В є не С. Отже, всі В є А.
7) Всі не В є А. Жодне А не є D. Всі В є С. Отже, всі D є С.
8) Всі D є Е. Всі С є А. Жодне В не є не D. Всі Е є не А. Отже, деякі А є D.
9) Всі А є В. Деякі В є С. Отже, існує А, таке що В і С.
10) Деякі С є D. Всі А є D. Всі В є не С. Отже, всі В є А.
11) Жодне с не є d. Всі а є d. Всі в є с. Отже, всі в не є а.
12) Всі С не є D. Всі А є не D. Всі В є С. Отже, всі В є А.
13) Деякі с не є d. Всі а є не d. Всі в є с. Отже, всі в є а.
14) Всі А є не В. Деякі В є С. Отже, не існує А, таких що В або С.
15) Деякі с не є d. Всі а є d. Всі в є не с. Отже, всі в є а.
16) Жодне С не є D. Всі А є D. Деякі В є С. Отже, всі В є А.
17) Всі не В є А. Жодне А не є D. Всі В є С. Отже, всі D є C.
18) Всі D є не Е. Всі С є А. Жодне В не є D. Всі Е є А. Отже, деякі А є D.
19) Не всі С є D. Всі А є D. Всі В є не С. Отже, деякі В є А.
20) Всі С є D. Деякі А є D. Всі не В є С. Отже, всі В є А.
21) Жодне С не є D. Всі А є D. Деякі В є С. Отже, всі В не є А.
22) Всі С є не D. Всі А є D. Всі В є С. Отже, деякі В є не А.
23) Деякі С є D. Всі А є не D. Всі В є С. Отже, всі В є А.
24) Жодне С не є D. Всі А є D. Всі В є С. Отже, деякі В є А.
ІІІ. Побудувати виведення в численні предикатів:
1)
├
![]() .
.
2)
├
![]() .
.
3)
├
![]() .
.
4)
├
![]() .
.
5)
├
![]() .
.
6)
├
![]() .
.
7)
├
![]() .
.
8)
├
![]() .
.
9)
├
![]() .
.
10)├
![]() ,
якщо х
не вільна в В.
,
якщо х
не вільна в В.
11)├ , Якщо х не вільна в в.
12)├ , Якщо х не вільна в в.
13)├
![]() .
.
14)├
![]() .
.
15)├
![]() .
.
16)├
![]() .
.
17)├
![]() .
.
18)├
![]() .
.
19)├
![]() .
.
20)├
![]() .
.
21)├
![]() .
.
22)├ , Якщо х не вільна в в.
23)├ .
24)├ .
ІV. Встановити, чи рівносильні формули в тризначній логіці
Лукасевича:
1)
![]() .
.
2)
![]() .
.
3)
![]() .
.
4)
![]() .
.
5)
![]() .
.
6)
![]() .
.
7)
![]() .
.
8)
![]() .
.
9)
![]() .
.
10)
![]() .
.
11)
![]() .
.
12)
![]() .
.
13)
![]() .
.
14) .
15)
![]() .
.
16)
![]() .
.
17)
![]() .
.
18)
![]() .
.
19)
![]() .
.
20)
![]() .
.
21)
![]() .
.
22)
![]() .
.
23) .
24)
![]() .
.
V. Довести примітивну рекурсивність функцій:
-
1)
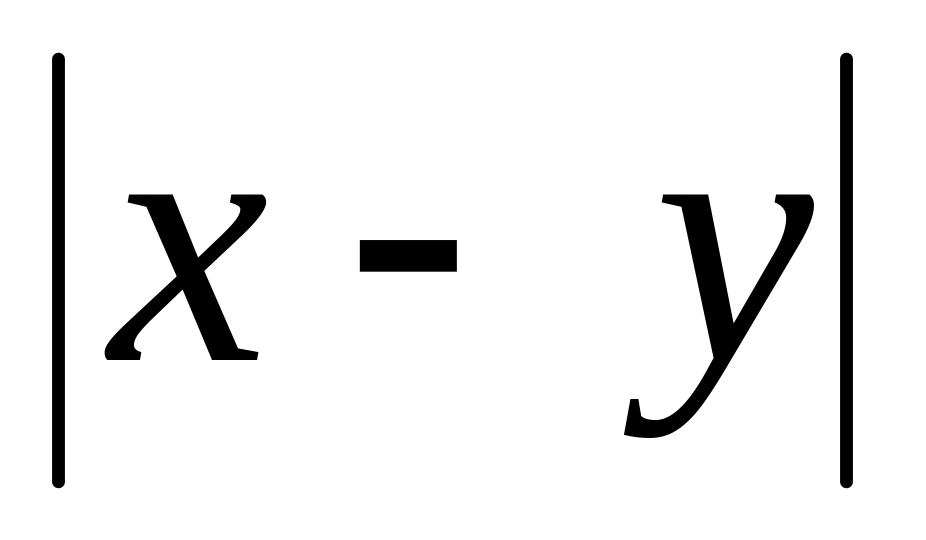 .
.2)
 .
.3)
 .
.4)
 .
.5)
 .
.6)
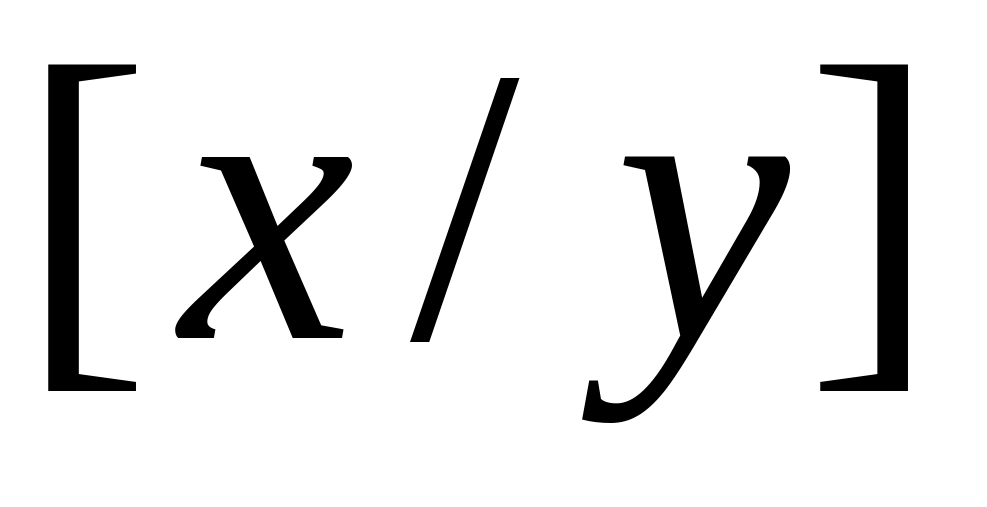 .
.7)
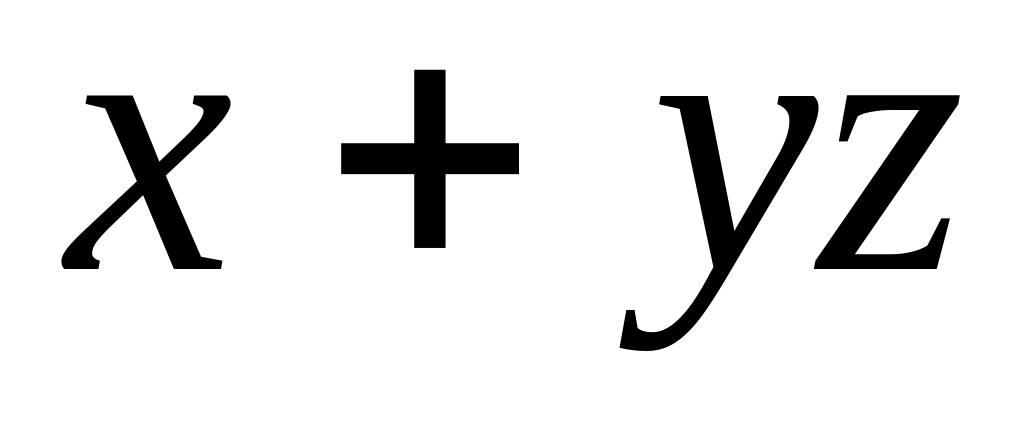 .
.8)
 .
.9)
 .
.10)
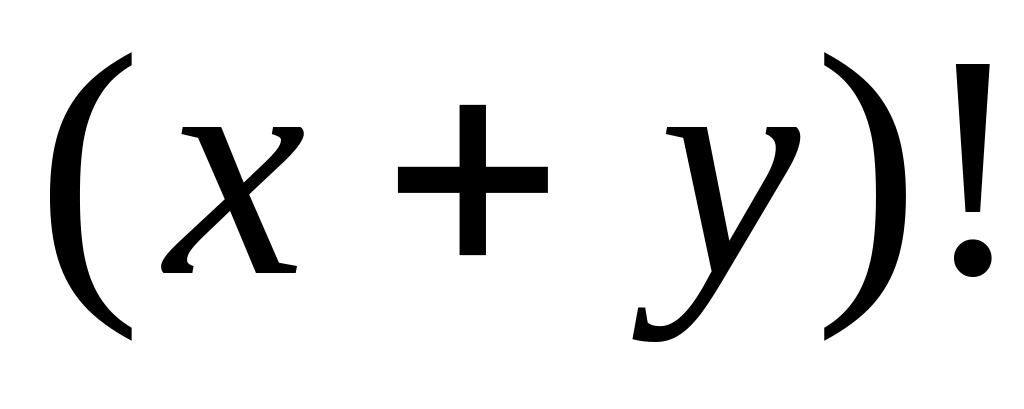 .
.11)
 .
.12)
 .
.13) .
14)
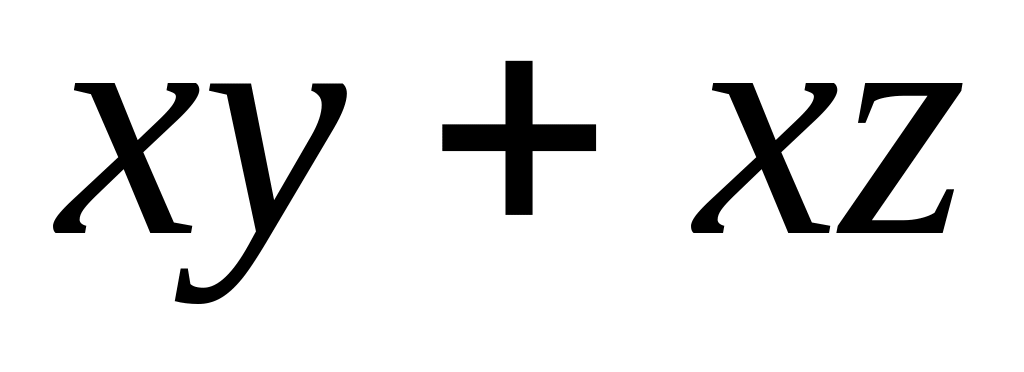 .
.15)
 .
.16)
 .
.17)
 .
.18)
 .
.19)
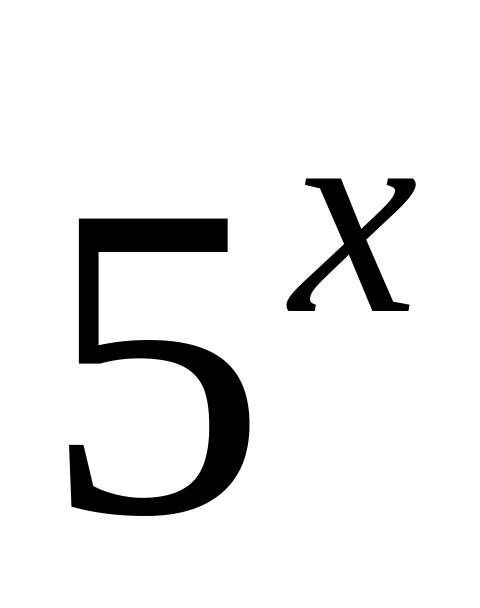 .
.20)
 .
.21)
 .
.22)
 .
.23)
 .
.24)
 .
.
