
- •Н. В. Бердинская, о. Ю. Павловская, д. В. Постников волновая оптика Практикум по решению задач
- •Введение
- •1. Явление интерференции света
- •1.1. Краткие теоретические сведения для решения задач
- •1.2. Примеры решения задач
- •1.3. Задачи, рекомендуемые для решения на аудиторных занятиях
- •1.4. Задачи для самостоятельного решения
- •2. Дифракция света. Поляризация световых волн
- •2.1. Краткие теоретические сведения для решения задач
- •2.1.1. Дифракция света
- •2.1.2. Поляризация световых волн
- •2.2. Примеры решения задач
- •2.3. Задачи, рекомендуемые для решения на аудиторных занятиях
- •2.4. Задачи для самостоятельного решения
- •Варианты домашнего задания
- •Библиографический список
1.2. Примеры решения задач
Задача
1. В опыте
Юнга расстояние между щелями
![]() ,
расстояние от щелей до экрана
,
расстояние от щелей до экрана
![]() .
Щели освещаются монохроматическим
светом с длиной волны
.
Щели освещаются монохроматическим
светом с длиной волны
![]() .
Определить расстояние между темными
полосами третьего порядка, расположенными
симметрично относительно центральной
полосы. Сколько темных полос находится
на центральном участке интерференционной
картины протяженностью 9,75 мм, если по
краям участка находятся темные полосы.
Какой должна быть толщина прозрачной
пластинки, с показателем преломления
n=1,6,
помещенной на пути одного из
интерференционных лучей, чтобы в
интерференционной картине на экране
первая светлая полоса сместилась на
место шестой темной?
.
Определить расстояние между темными
полосами третьего порядка, расположенными
симметрично относительно центральной
полосы. Сколько темных полос находится
на центральном участке интерференционной
картины протяженностью 9,75 мм, если по
краям участка находятся темные полосы.
Какой должна быть толщина прозрачной
пластинки, с показателем преломления
n=1,6,
помещенной на пути одного из
интерференционных лучей, чтобы в
интерференционной картине на экране
первая светлая полоса сместилась на
место шестой темной?
Дано: |
Решение |
= 650 нм = 65·10-8 м |
На пути световой волны, идущей от источника света S (рис.1.1) Юнг поместил экран с одной щелью, а за ним экран с двумя щелями расположенными симметрично. Полусферическая волна, идущая от первой щели, одновременно достигает двух щелей. Образуются две когерентные волны. Опыт Юнга можно представить в виде следующей схемы: источники света S1 и S2 находятся на расстоянии d друг от друга (рис.1.1). |
d =2 мм = 2·10-3 м |
|
L=4 м |
|
S = 9,75мм = 9,75·10-3 м |
|
n = 1,6 |
|
N = 10 |
|
Z3-3 - ? NТ - ? h - ? |
|
На
экране Э, который находится на расстоянии
L
от источников, наблюдается
интерференционная картина в виде
чередующихся светлых и темных полос,
параллельных щелям. В центре
интерференционной картины расположена
светлая полоса. Опыт выполняется при
условии, что
1)
Проведем расчет интерференционной
картины. Рассмотрим одну из
интерференционных полос, расположенную
в точке М на расстоянии Z
от центра экрана т. О (рис.1.1). Найдем
связь оптической разности хода лучей
с параметрами установки. ИзMS1A:
ИзS2MB:
Темная
полоса в точке М будет наблюдаться
при выполнении условия
2)
Аналогично расстояние от центра экрана
до светлой полосы определяется из
условия (1.2)
3)
Если на пути одного из интерферирующих
лучей поместить прозрачную пластинку,
то изменится оптическая разность хода
лучей (рис. 1.1). Оптический путь первого
луча останется равным его геометрическому
пути l1'
=r1
, а оптический путь второго луча станет
равным
Отсюда
Ответ: 1) Z3-3 = 6,5мм. 2) NТ = 8. 3) h = 5,85мкм. |
|
Задача
2. На поверхность
стеклянного объектива (![]() )
нанесена тонкая прозрачная пленка (
)
нанесена тонкая прозрачная пленка (![]() ).
Пленка освещается параллельным пучком
белого света, падающим на нее под углом
450
. Найти минимальную толщину пленки, при
которой в проходящем свете она будет
окрашена в желтый цвет (
).
Пленка освещается параллельным пучком
белого света, падающим на нее под углом
450
. Найти минимальную толщину пленки, при
которой в проходящем свете она будет
окрашена в желтый цвет (![]() ).
).
Дано: n2 = 1,5 n1 = 1,6 = 450 = 0,785 рад = 580 нм = 58·10-8 м |
Решение Пусть на тонкую прозрачную пленку толщиной h и показателем преломления n падает плоская световая волна, образующая угол с нормалью (рис. 1.2). Представим волну одним лучом. На верхней поверхности волна частично отразится под углом , частично преломится под углом и пройдет внутрь пленки. |
hmin - ? |
В
точке А волна касается второй поверхности,
где она частично отразится, а частично
преломится и выйдет из тонкой пленки.
В точке В волна снова разделится на две
части и т. д. В результате многократного
отражения и преломления падающая на
пленку волна разделится на ряд волн,
отраженных и проходящих ч ерез
пленку. При наложении волны интерферируют.
Волны, получившиеся в результате
3–5–кратного отражения и т. д., имеют
очень малую интенсивность, и при расчете
интерференционной картины мы их учитывать
не будем. Рассмотрим только те лучи
(1',2'), которые участвуют в образовании
интерференционной картины в проходящем
свете. По условию задачи пленка в
проходящем свете окрашена в желтый
цвет. Это означает, что для лучей желтого
света выполняется условие максимума.
Найдем оптическую разность хода для
лучей 1' и 2'. Оптический путь луча будет
считаться от точки О до фронта преломленной
волны DC.
Для луча 1':
ерез
пленку. При наложении волны интерферируют.
Волны, получившиеся в результате
3–5–кратного отражения и т. д., имеют
очень малую интенсивность, и при расчете
интерференционной картины мы их учитывать
не будем. Рассмотрим только те лучи
(1',2'), которые участвуют в образовании
интерференционной картины в проходящем
свете. По условию задачи пленка в
проходящем свете окрашена в желтый
цвет. Это означает, что для лучей желтого
света выполняется условие максимума.
Найдем оптическую разность хода для
лучей 1' и 2'. Оптический путь луча будет
считаться от точки О до фронта преломленной
волны DC.
Для луча 1':
![]() . Для луча 2':
. Для луча 2':
![]() В точках А и В луч отражается от сред с
меньшим показателем преломления, поэтому
потери
В точках А и В луч отражается от сред с
меньшим показателем преломления, поэтому
потери
![]() не происходит. Оптическая разность хода
лучей 1' и 2'
не происходит. Оптическая разность хода
лучей 1' и 2'
![]() .
Из
AKB:
.
Из
AKB:
![]() ,
AB=BC.
Из
AСD
,
AB=BC.
Из
AСD
![]() ,
,
![]() .
Из закона преломления света
.
Из закона преломления света
![]() .
Таким образом
.
Таким образом
![]() .
.
Используя условие максимума интерференции:
![]() ,
где m
= 1,2,3, ….
,
где m
= 1,2,3, ….
Очевидно,
минимальной толщине пленки соответствует
m=1
![]() .
Отсюда
.
Отсюда
 .
Подставим числовые данные задачи: hmin
= 0,2 мкм.
.
Подставим числовые данные задачи: hmin
= 0,2 мкм.
Ответ: hmin = 0,2 мкм.
Задача
3. На тонкий
стеклянный клин (![]() )
падает параллельный пучок монохроматического
света длиной волны
)
падает параллельный пучок монохроматического
света длиной волны
![]() под углом 45º. Угол между поверхностями
клина равен 0,51'. Найти, сколько темных
интерференционных полос наблюдается
в отраженном свете на поверхности клина
длиной
под углом 45º. Угол между поверхностями
клина равен 0,51'. Найти, сколько темных
интерференционных полос наблюдается
в отраженном свете на поверхности клина
длиной
![]() ,
если по краям наблюдаемого участка
расположены светлые полосы.
,
если по краям наблюдаемого участка
расположены светлые полосы.
О
т
На
участке
Ответ: NТ = 10.
|
Задача
4. Плосковыпуклая
стеклянная линза с радиусом кривизны
сферической поверхности
![]() прижата к стеклянной пластинке (
прижата к стеклянной пластинке (![]() ).
Диаметр пятнадцатого темного кольца
Ньютона в отраженном свете равен 6,4 мм.
Найти: 1) длину волны монохроматического
света, падающего на установку
перпендикулярно поверхности пластинки;
2) диаметр третьего светлого кольца
Ньютона в проходящем свете.
).
Диаметр пятнадцатого темного кольца
Ньютона в отраженном свете равен 6,4 мм.
Найти: 1) длину волны монохроматического
света, падающего на установку
перпендикулярно поверхности пластинки;
2) диаметр третьего светлого кольца
Ньютона в проходящем свете.
Дано: |
Решение |
d=6,4мм = 6,410-3 м |
Явление интерференции света можно наблюдать и на установке предложенной Ньютоном, которая состоит из плосковыпуклой линзы большого радиуса кривизны R (рис. 1.5), соприкасающейся с плоской отполированной пластинкой. Остающаяся между ними прослойка из воды имеет форму клина. При освещении установки монохроматическим светом, направленным перпендикулярно поверхности пластинки, наблюдается интерференционная |
R = 1,25 м |
|
n3 = 1,5 |
|
n2 = 1,33 |
|
n1 = 1 |
|
- ? d - ? |
|
Отсюда
Из OAB
Толщина
клина h
– величина очень маленькая, поэтому
членом h2
можно пренебречь. Из (1.5) и (1.6)
Ответ: 1) 726 нм; 2) d = 1,43 мм. |
|



 птический
путь луча 1’, отраженного от верхней
поверхности клина:
птический
путь луча 1’, отраженного от верхней
поверхности клина:
 огда
огда
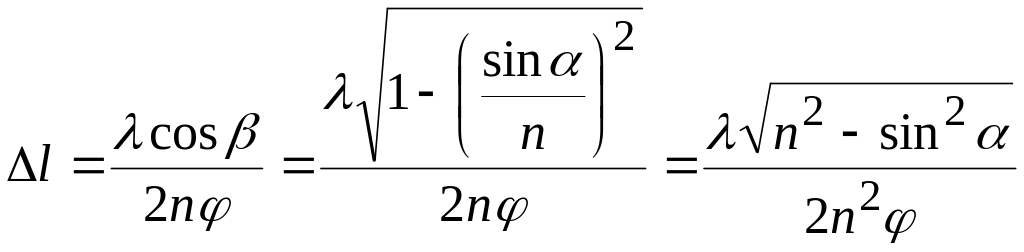 .
. картина
в виде системы чередующихся темных и
светлых полос, называемых кольцами
Ньютона. Пространство между линзой и
пластинкой заполнено жидкостью. Кольца
Ньютона наблюдаются как в отраженном,
так и проходящем свете. Проследим ход
одного из лучей, упавшего на поверхность
водяного клина в точку В. Он частично
отражается от верхней поверхности
клина (т. В), частично проходит внутрь
клина и, отражаясь от поверхности
стеклянной пластинки (т. D),
возвращается назад, образуя два
когерентных луча 1 и 2 направленных
перпендикулярно к поверхности
пластинки. Найдем оптическую разность
хода этих лучей. Луч 1 отражается от
раздела границы стекла (n3)
с водой (n2).
Так как n2<
n3,
потери
картина
в виде системы чередующихся темных и
светлых полос, называемых кольцами
Ньютона. Пространство между линзой и
пластинкой заполнено жидкостью. Кольца
Ньютона наблюдаются как в отраженном,
так и проходящем свете. Проследим ход
одного из лучей, упавшего на поверхность
водяного клина в точку В. Он частично
отражается от верхней поверхности
клина (т. В), частично проходит внутрь
клина и, отражаясь от поверхности
стеклянной пластинки (т. D),
возвращается назад, образуя два
когерентных луча 1 и 2 направленных
перпендикулярно к поверхности
пластинки. Найдем оптическую разность
хода этих лучей. Луч 1 отражается от
раздела границы стекла (n3)
с водой (n2).
Так как n2<
n3,
потери