
- •Математика Интегральное исчисление
- •I курса очной формыобучения
- •Предисловие
- •Оглавление
- •Глава 1 Неопределенный интеграл………………………………..5
- •Глава 2. Определенный интеграл………………………………….17
- •Глава 3. Кратные интегралы………………………………………23
- •Глава 4. Криволинейные интегралы………………………………29
- •Глава 1. Неопределенный интеграл
- •1.5. Метод интегрирования по частям
- •1.6. Интегрирование рациональных функций
- •1.7. Интегрирование тригонометрических функций
- •1.8. Интегрирование иррациональных функций
- •Глава 2. Определенный интеграл
- •2.1. Определение и вычисление определенного интеграла
- •2.2. Замена переменной и интегрирование по частям в определенном интеграле
- •2.3. Применение определенного интеграла
- •2.3.1. Полярная система координат
- •2.3.2. Вычисление площадей фигур
- •2.3.3. Вычисление длины дуги плоской кривой
- •2.3.4. Вычисление объема тел вращения
- •2.4. Несобственные интегралы
- •Глава 3. Кратные интегралы
- •3.1. Двойной интеграл
- •3.2. Применение двойного интеграла
- •3.3. Двойной интеграл в полярных координатах
- •Глава 4. Криволинейные интегралы
- •4.1. Криволинейный интеграл I рода (по длине дуги)
- •Приложение криволинейного интеграла 1-го рода
- •4.2. Криволинейный интеграл II рода (по координатам)
- •Вычисление криволинейных интегралов II рода
- •Приложения криволинейного интеграла II рода
- •Список рекомендуемой литературы
1.8. Интегрирование иррациональных функций
Некоторые часто встречающиеся интегралы от иррациональных функций можно вычислить методом рационализации подынтегральной функции. Этот метод заключается в отыскании такой подстановки, которая преобразует интеграл от иррациональной функции в интеграл от функции рациональной. Можно выделить следующие типы интегралов от иррациональных функций:
1.
 .
Для таких интегралов рационализация
достигается подстановкой
.
Для таких интегралов рационализация
достигается подстановкой
 ,
гдеm
– общий знаменатель рациональных чисел
Р1,
Р2,…,
Pn.
,
гдеm
– общий знаменатель рациональных чисел
Р1,
Р2,…,
Pn.
2. Интегралы типа

 сводятся к табличным
после выделения под радикалами полного
квадрата и последующей подстановкой
сводятся к табличным
после выделения под радикалами полного
квадрата и последующей подстановкой
 .
.
3. Интегралы типа

 приводятся к
рационально зависящим от тригонометрических
функций выражениям с помощью следующих
тригонометрических подстановок
соответственно: х=asint
или x=acost,
x=atgt,
приводятся к
рационально зависящим от тригонометрических
функций выражениям с помощью следующих
тригонометрических подстановок
соответственно: х=asint
или x=acost,
x=atgt,
 .
.
________________________
Найти интегралы:
1.
 ;
2.
;
2.
 ;
3.
;
3.
 ;
;
4.
 ;
5.
;
5.
 ;
6.
;
6.
 ;
;
7.
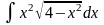 ;
8.
;
8.
 ;
9.
;
9.
 ;
10.
;
10.
 ;
;
11.
 ;
12.
;
12.
 .
.
Ответы:
1.
 ;
;
2.
 ;
;
3.
 ;
4.
;
4.
 ;
;
5.
 ;
;
6.
 ;
;
7.
 ;
8.
;
8.
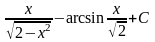 ;
;
9.
 ;
10.
;
10.
 ;
11.
;
11.
 ;
;
12.
 .
.
Глава 2. Определенный интеграл
2.1. Определение и вычисление определенного интеграла
Пусть на отрезке
[a,b]
определена функция f(x).
Разобьем отрезок [a,b]
на n
частей точками a=x0<x1<…<xn=b
и на каждом интервале (xi-1,xi)
выберем произвольную точку i.
Составим сумму
 ,
где xi=xi
-xi-1,
которая называется интегральной суммой.
,
где xi=xi
-xi-1,
которая называется интегральной суммой.
Предел
 называется определен-ным интегралом
от функции f(x)
в пределах от а
до b.
Вычисляется определенный интеграл по
формуле Ньютона-Лейбница, т.е.
называется определен-ным интегралом
от функции f(x)
в пределах от а
до b.
Вычисляется определенный интеграл по
формуле Ньютона-Лейбница, т.е.
 значения
первообразной функции для f(x)
в точках верхнего и нижнего пределов.
значения
первообразной функции для f(x)
в точках верхнего и нижнего пределов.
2.2. Замена переменной и интегрирование по частям в определенном интеграле
Пусть функция x=(t) и ее производная x'='(t)непрерывны при t[,], и множеством значений функции x=(t) при t[,] является отрезок [a,b], и пусть()=а, ()=b, тогда
 или
или
 .
.
Эта формула называется формулой замены переменной в определенном интеграле.
Интегрирование по частям в определенном интеграле осуществляется по следующей формуле:
 .
.
___________________
Вычислить определенные интегралы:
1.
 ;
2.
;
2.
 ;
3.
;
3.
 ;
4.
;
4.
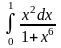 ;
5.
;
5.
 ;
;
6.
 ;
7.
;
7.
 ;
8.
;
8.
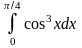 ;
9.
;
9.
 ;
10.
;
10.
 ;
;
11.
 ;
12.
;
12.
 .
.
Ответы:
1. 0; 2.
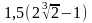 ;
3. /6;
4. /12;
5. ;
6. 7+2ln2;
7.
;
3. /6;
4. /12;
5. ;
6. 7+2ln2;
7.
 ;
;
8.
 ;
9.
;
9.
 ;
10.
;
10.
 ;
11.
;
11.
 ;
12.
;
12.
 .
.
2.3. Применение определенного интеграла
2.3.1. Полярная система координат
Как известно, положение точки М на плоскости в прямоугольной системе координат определяется парой чисел (х,у) – координатами точки.
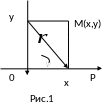 В
полярной системе координат та же точка
может быть определена так называемым
полярным углом
и длиной радиуса – вектора
В
полярной системе координат та же точка
может быть определена так называемым
полярным углом
и длиной радиуса – вектора
 (рис.1). Луч ОР
называется полярной осью, т.О – полюсом.
Связь между декартовым и полярными
координатами состоит в следующем:
(рис.1). Луч ОР
называется полярной осью, т.О – полюсом.
Связь между декартовым и полярными
координатами состоит в следующем:
 ;
;
 .
.
Построить кривые, заданные уравнением в полярной системе координат:
1. r=a; 2. r=3(1-cos); 3. r=asin3; 4. r=acos2; 5. r2=a2cos2.
