
- •Математика Интегральное исчисление
- •I курса очной формыобучения
- •Предисловие
- •Оглавление
- •Глава 1 Неопределенный интеграл………………………………..5
- •Глава 2. Определенный интеграл………………………………….17
- •Глава 3. Кратные интегралы………………………………………23
- •Глава 4. Криволинейные интегралы………………………………29
- •Глава 1. Неопределенный интеграл
- •1.5. Метод интегрирования по частям
- •1.6. Интегрирование рациональных функций
- •1.7. Интегрирование тригонометрических функций
- •1.8. Интегрирование иррациональных функций
- •Глава 2. Определенный интеграл
- •2.1. Определение и вычисление определенного интеграла
- •2.2. Замена переменной и интегрирование по частям в определенном интеграле
- •2.3. Применение определенного интеграла
- •2.3.1. Полярная система координат
- •2.3.2. Вычисление площадей фигур
- •2.3.3. Вычисление длины дуги плоской кривой
- •2.3.4. Вычисление объема тел вращения
- •2.4. Несобственные интегралы
- •Глава 3. Кратные интегралы
- •3.1. Двойной интеграл
- •3.2. Применение двойного интеграла
- •3.3. Двойной интеграл в полярных координатах
- •Глава 4. Криволинейные интегралы
- •4.1. Криволинейный интеграл I рода (по длине дуги)
- •Приложение криволинейного интеграла 1-го рода
- •4.2. Криволинейный интеграл II рода (по координатам)
- •Вычисление криволинейных интегралов II рода
- •Приложения криволинейного интеграла II рода
- •Список рекомендуемой литературы
1.5. Метод интегрирования по частям
Пусть u=u(x) и v=v(x) – дифференцируемые функции, тогда d(uv)=udv+vduи
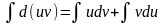 или
или
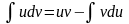 .
.
Полученная формула называется формулой интегрирования по частям.
Выделим три типа интегралов, для которых метод интегрирования по частям наиболее эффективен
I.
 где Pn(x)
– многочлен n-й
степени. За функцию u
принимается многочлен Pn(x),
dv
– все остальные сомножители. Формула
интегрирования по частям применяется
последовательно n
раз.
где Pn(x)
– многочлен n-й
степени. За функцию u
принимается многочлен Pn(x),
dv
– все остальные сомножители. Формула
интегрирования по частям применяется
последовательно n
раз.
II.
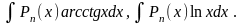 Pn(x)dx=dv,
за u
принимаются осталь-ные сомножители.
Pn(x)dx=dv,
за u
принимаются осталь-ные сомножители.
III.
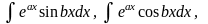 гдеa,
b
– действительные числа.
гдеa,
b
– действительные числа.
За u(x) можно принимать любую из двух функций. Формулу интегрирования по частям нужно применить дважды. Каждый раз за функцию u(x) принимается одинаковая по типу функция.
_________________
Найти интегралы:
1.
|
2.
|
3.
|
4.
|
5.
|
6.
|
7.
|
8.
|
9.
|
10.
|
11.
|
12.
|
13.
|
14.
|
Ответы:
1.
–xcosx+sinx+C;
2.
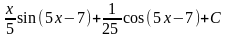 ;
;
3.
(x2-2x+2)ex+C ;
4.
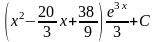 ;
;
5.
 ;
6. x2sinx+2xcosx-2sinx+C ;
7. xlnx-x+C ;
;
6. x2sinx+2xcosx-2sinx+C ;
7. xlnx-x+C ;
8.
 ;
9. xarcsinx+
;
9. xarcsinx+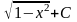 ;
;
10.
 ;
11. xtgx+ln|cosx|+C ;
;
11. xtgx+ln|cosx|+C ;
12.
 ;
;
13.
0,5lx(sinx+cosx)+C ;
14.
 .
.
1.6. Интегрирование рациональных функций
Дробно-рациональной
функцией (рациональной дробью) называется
функция, равная отношению двух многочленов:
 ,
где Pn(x),
Qm(x)
– многочлены степени n
и m
соответственно.
,
где Pn(x),
Qm(x)
– многочлены степени n
и m
соответственно.
Рациональная дробь называется правильной, если степень многочлена числителя меньше степени многочлена знаменателя.
Из неправильной дроби всегда можно выделить целую часть, интегрирование которой трудностей не составляет.
Любую правильную
рациональную дробь
 ,
знаменатель которой разложен на множители
как
,
знаменатель которой разложен на множители
как

можно представить в виде суммы простейших дробей следующим образом:


_____________
Найти интегралы:
1.
|
2.
|
3.
|
4.
|
5.
|
6.
|
7.
|
8.
|
9.
|
10.
|
11.
|
12.
|
13.
|
14. . |
Ответы:
1.
 ;
2.
;
2.
 ;
3.
;
3.
 ;
;
4.
 ;
5.
;
5.
 ;
6.
;
6.
 ;
;
7. ;8.x+3ln(x2-6x+10)+8arctg(x-3)+C;
9.
;8.x+3ln(x2-6x+10)+8arctg(x-3)+C;
9.
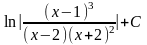 ;
10.
;
10.
 ;
;
11.
 ;
;
12.
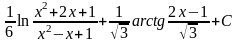 ;
;
13.
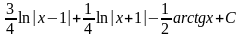 ;
;
14.
 .
.
1.7. Интегрирование тригонометрических функций
Функция с переменными sinx и cosx, над которыми выполняются операции сложения, вычитания, умножения и деления, называется рациональной функцией и обозначается как R(sinx, cosx).
В процессе интегрирования различных тригонометрических выражений часто используются известные тригонометрические формулы:
 .
(1)
.
(1)
 .
(2)
.
(2)
 .
(3)
.
(3)
Можно выделить несколько типов интегралов от тригонометрических функций:
1.
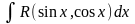 .
Он находится с помощью универсальной
тригонометрической подстановки:
.
Он находится с помощью универсальной
тригонометрической подстановки:
 .
.
2. Если подынтегральная функция R(sin x, cos x) нечетна относительно sin x, то можно cos x принять за t; если она нечетна относительно cos x, то за t принимается sin x.
3. Если подынтегральная
функция четна относительно sin x
и cos x,
то за переменную t
принимается tgx,
т.е. tgx=t;
x=arctgt,
 ;
sin2x=
;
sin2x= .
.
4.
 находятся после понижения степени
подынтегральной функции.
находятся после понижения степени
подынтегральной функции.
5.
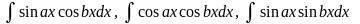 вычисляются
после применения к подынтегральным
функциям формул (3).
вычисляются
после применения к подынтегральным
функциям формул (3).
____________________
Найти интегралы:
1.
|
2.
|
3.
|
4.
|
5.
|
6.
|
7.
|
8.
|
9.
|
10.
|
11.
|
12.
|
13.
|
14.
|
15.
|
16.
|
Ответы:
1.
 ;
2.
;
2.
 ;
3.
;
3.
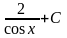 ;
;
4.
 ;
5.
;
5.
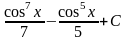 ;
;
6.
 ;
7.
;
7.
 ;
;
8.
 ;
9.
;
9.
 ;
;
10.
 ;
11.
;
11. ;
;
12.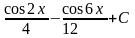 ;
13.
;
13.
 ;
;
14.
 или
или
 ;
15.
;
15.
 ;
;
16.
 .
.

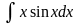 .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
.
 .
.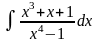 .
. ;
; ;
; ;
; ;
; ;
; ;
;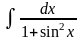 ;
; ;
;
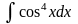 ;
; ;
; ;
; ;
; ;
; ;
; .
.