Сохоцкого формулы

- формулы, найденные впервые Ю. В. Сохоцким [1] и выражающие граничные значения интеграла типа Коши. С более полными доказательствами, но значительно позже С. ф. были получены независимо Й. Племелем [2]. Пусть Г : t=t(s), t(0)=t(l), - замкнутая гладкая жордаиова кривая на плоскости комплексного неременного - заданная на Г комплексная плотность интеграла типа Коши, относительно к-рой предполагается, что она удовлетворяет условию Гёльдера

D⁺ - область внутри Г , D ^-- внешняя область;

- интеграл типа Коши. Тогда для любой точки существуют пределы

к-рые выражаются формулами Сохоцкого

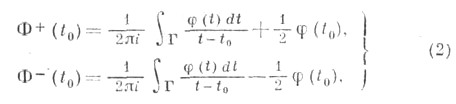
или, иначе,

Интеграл вдоль Г в правых частях С. ф. понимается в смысле главного значения по Коши и наз. сингулярным интегралом. Таким образом, принимая при высказанных условиях Ф+(t)(или Ф ^-(t)) в качестве значений интеграла Ф(z) на Г , получают функцию Ф(z), непрерывную в замкнутой области (соответственно в в целом Ф(z) иногда описывают как кусочно аналитич. цию. Если то Ф ⁺(t)и Ф ^-(t) также непрерывны по Гёльдеру на Г с тем же показателем а если то с любым показателем Для угловых точек t₀ (см. рис.) кусочно гладкой кривой Г С. ф. принимают вид

В случае разомкнутой кусочно гладкой кривой Г С. ф. (2) и (3) остаются в силе для внутренних точек дуги Г. С. ф. играют основную роль при решении граничных задач теории функций и сингулярных интегральных уравнений (см. [3], [5]), а также при решении различных прикладных задач теории функций (см. [4]).

Естественно возникает вопрос о возможном расширении условий на контур Г и плотность с тем, чтобы С. ф., хотя бы с нек-рыми оговорками, сохраняли силу. Наиболее значительные результаты в этом направлении принадлежат В. В. Голубеву и И. И. Привалову (см. [6], [8]). Напр., пусть Г - спрямляемая жорданова кривая, а плотность по-прежнему непрерывна по Гёльдеру на Г. Тогда С. ф. (2) имеют место почти всюду на Г, причем под Ф ⁺(t₀) и Ф ^-(t₀) понимаются угловые граничные значения интеграла типа Коши соответственно изнутри и извне Г, но функции Ф ⁺(z) и Ф ^- (z), вообще говоря, уже не непрерывны в замкнутых областях О пространственных аналогах С. ф. см. в [7].

Аналитическое продолжение

В комплексном анализе аналитическим продолжением функции , определённой на множестве , называется аналитическая функция, которая:

• определена на более широком множестве , содержащем ;

• в области совпадает с исходной функцией .

Определение

Задача нахождения аналитического продолжения функции, определённой на некотором множестве, заключается в таком распространении определения этой функции на возможно более широкую область, при котором она была бы аналитической и в новой области. Простейшим примером аналитического продолжения может служить переход от функций действительного переменного (то есть функций, определённых только на действительной оси) к функциям комплексного переменного, аналитическим во всей (или почти во всей) плоскости и совпадающим с соответствующими функциями действительного переменного при действительных значениях аргумента.

Для каждой конкретной аналитической функции существование и единственность аналитического продолжения определяются теоремой единственности