8.7. Учет временной стоимости денег в управлении денежными потоками

 

Необходимость учета временной стоимости денег в управлении финансовыми ресурсами и денежными потоками вытекает из самой природы проведения различных финансовых операций, инвестирования денежных средств и связана с двумя основными факторами: обесценением денежных средств в процессе инфляции и их способностью приносить дополнительный доход в случае пуска в оборот.

Для учета фактора времени в финансовом менеджменте используют операции дисконтирования и наращения. Данные методы предназначены для приведения денежных средств, получаемых в разные периоды к требуемому моменту времени в настоящем или будущем. Данные операции осуществляются с использованием процентной ставки (r). С точки зрения финансового менеджмента процентная ставка может выступать в качестве нормы доходности от проводимых операций или в качестве альтернативы показателя стоимости капитала. Наращение – это процесс, в котором заданы исходная сумма (PV) и процентная ставка. Смысл операции наращения состоит в определении величины той суммы, которой будет или желает располагать инвестор по окончании операции (FV).

Дисконтирование – это процесс, котором заданы ожидаемая в будущем к получению сумма (FV) и ставка. Смысл операции дисконтирования заключается в определении величины текущей суммы (PV), которую необходимо иметь сейчас для получения ожидаемой суммы в будущем (FV).

Графически операции дисконтирования и наращения выглядят следующим образом.

 

 

 

PV – текущая сумма;

FV – будущая сумма;

I = FV – PV – приращение капитала;

 

Простые и сложные проценты

 

В теории и практике финансово-экономических расчетов принято выделять две схемы начисления процентов:

  Простые проценты – предполагают неизменность величины, с которой происходит начисление, т.е. сумма процента, начисленного в предыдущем периоде, не принимается в расчет в процессе последующего наращения.

  Сложные проценты – предполагают увеличение базы, с которой происходит начисление с каждым шагом времени, т.е. сумма процента, начисленного в предыдущем периоде, присоединяется к основной сумме долга в процессе последующего наращения (капитализируется).

 

Наращение по простому проценту выглядит следующим образом:

 

, где

 

r – процентная ставка;

n – длительность операции (под ней чаще всего подразумевают целое количество лет).

В случае, если длительность операции не равна целому количеству лет, вместо n используют показатель:  , где T – количество дней в году.

Дисконтирование по простому проценту можно представить следующим образом:

 

 

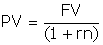
Эта операция называется математическим дисконтированием.

Однако, в практике финансово-экономических расчетов используют еще один вид дисконтирования – банковское дисконтирование, применяющееся, как правило, при учете банком векселей. В этом случае вместо процентной ставки r используют дисконтную (учетную) ставку d. Таким образом, операция дисконтирования выглядит следующим образом:

 

 

Наращение с использованием сложной схемы начисления процентов можно представить следующим образом:

 

 

Выразив из этой формулы показатель текущей стоимости, можно аналогично осуществить процесс математического дисконтирования:

 

 

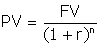
Таким же образом можно представить процесс банковского дисконтирования:  .

В том случае если продолжительность финансовой операции не равна целому количеству лет используют две схемы начисления сложных процентов:

 Сложную – 

 Смешанную –  , где

w – целое число лет, а f – дробная часть

 

Графически связь между простой и сложной схемой начисления процентов можно представить следующим образом.

 

 

При периоде менее 1 года более выгодна схема начисления простого процента. При периоде более 1 года – схема начисления сложного процента. Если период равен 1 году, то обе схемы дают одинаковый результат.