
X0пр1, x0пр2 – начальная координата пути смещения груза на пружине 1 и 2.
Таблица 2
N |
1 |
2 |
3 |
4 |
5 |
nпр1 |
15 |
16 |
15 |
17 |
16 |
nпр2 |
22 |
21 |
23 |
22 |
21 |
где nпр1, nпр2 – число колебаний, за которое амплитуда колебаний измениться
с 20мм до 15мм.
Таблица 3
N |
1 |
2 |
3 |
4 |
5 |
||||||
ti,c |
m=600г |
5,66 |
5,71 |
5,62 |
5,60 |
5,64 |
|||||
m=500г |
5,21 |
5,19 |
5,21 |
5,23 |
5,19 |
||||||
m=400г |
4,77 |
4,71 |
4,74 |
4,73 |
4,76 |
||||||
m=300г |
4,08 |
4,10 |
4,12 |
4,15 |
4,10 |
||||||
где ti – время 10 колебаний, при весе груза m.
Вычисление:
Находим коэффициент жесткости для пружины 1:
для массы 200г

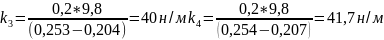
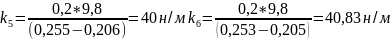
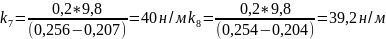

 н/м
н/м
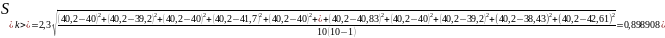 н/м
н/м
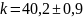 н/м
н/м
для массы 400г

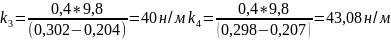
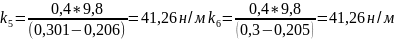

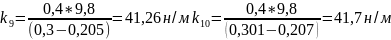
 н/м
н/м
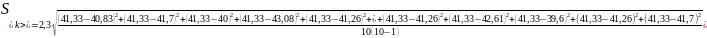 =
=
=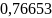 н/м
н/м
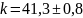 н/м
н/м
для массы 600г
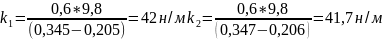
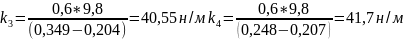


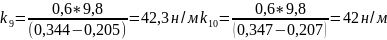
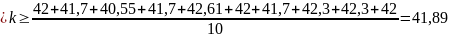 н/м
н/м
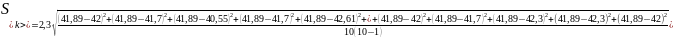 =
=
=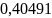 н/м
н/м
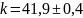 н/м
н/м
Находим коэффициент жесткости для пружины 2:
для массы 200г
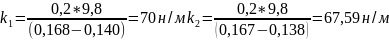
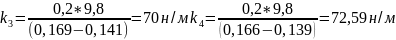
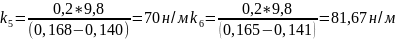
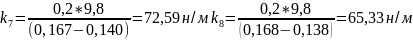
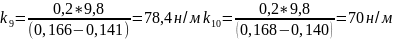
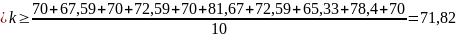 н/м
н/м
 =
=
 н/м
н/м
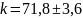 н/м
н/м
для массы 400г
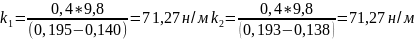
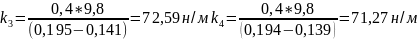
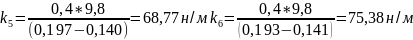
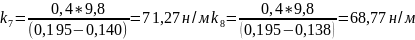
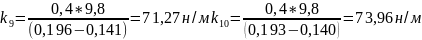
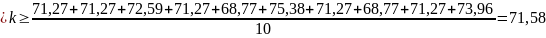 н/м
н/м
 =
=
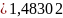 н/м
н/м
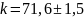 н/м
н/м
для массы 600г
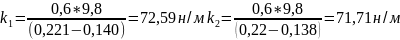
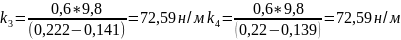

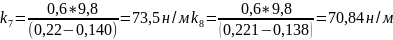

 н/м
н/м
 =
=
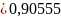 н/м
н/м
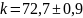 н/м
н/м
Определение логарифмического декремента затухания:
А1=20мм, А2=15мм.
для пружины 1
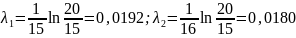 ;
;
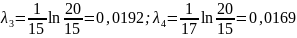 ;
;
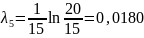 ;
;
<
>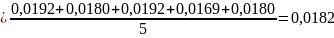
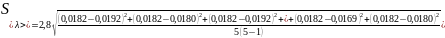 =0,001193424
=0,001193424
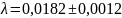
для пружины 2
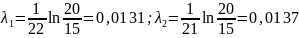 ;
;
 ;
;
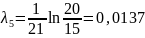 ;
;
<
>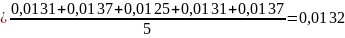
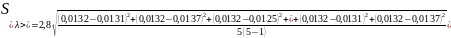 =0,000628318
=0,000628318
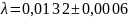
Определение коэффициента жесткости при динамическом нагружении:
для груза массой m=600г
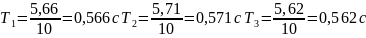
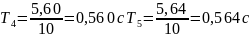
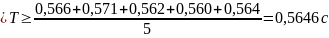
для груза массой m=500г
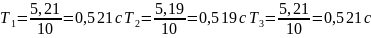

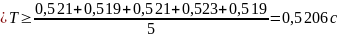
для груза массой m=400г
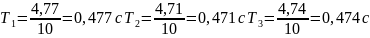
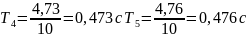

для груза массой m=300г

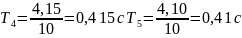
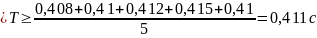

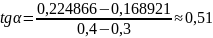


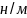
Вывод
и анализ результатов:
Я исследовал
зависимость параметров колебательного
движения от свойств пружины и выяснил,
что период колебания зависит от массы
подвешенного груза и коэффициента
жесткости пружины. Затем определил
логарифмический декремент затухания
пружинного маятника, который показывает
быстроту затухания колебаний. Полученные
значения жесткости пружины статическим
методом и из углового коэффициента ( )
сходятся лишь при массе 200г (
)
сходятся лишь при массе 200г (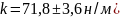 ,
а в остальных случаях (
,
а в остальных случаях (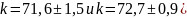 близки по значениям.
близки по значениям.
