Тема: Изучение собственных колебаний пружинного маятника.

Цель работы: Исследовать зависимость параметров колебательного движения от свойств пружины.

Приборы и принадлежности: набор пружин различной жесткости: длинная, короткая; штатив, секундомер, набор грузов различной массы.

Теоретическая часть:

1. Гармонические колебания — колебания, при которых колеблющаяся величина изменяется со временем по закону синуса (косинуса). Основными характеристиками колебаний является амплитуда, частота, период.

2. Пружинный маятник — это груз массой m, который подвешен на абсолютно упругой пружине и совершает гармонические колебания под действием упругой силы F = –kx, где k — жесткость пружины.

Период колебания пружинного маятника зависит от жесткости пружины k и массы груза m.

3. Затухающие колебания — колебания, энергия которых уменьшается с течением времени.

Получим дифференциальное уравнение свободных затухающих колебаний на примере реального пружинного маятника, совершающего колебания в среде с сопротивлением (простейший случай - трение о воздух). Пусть масса маятника m, коэффициент упругости пружины k, сила сопротивления, действующая на маятник, F = - bv, v - скорость маятника, b - коэффициент сопротивления среды, в которой находится маятник. Так как мы рассматриваем только линейные системы, b = const, k = const. x - смещение маятника от положения равновесия. Второй закон Ньютона в нашем случае запишется так:

Это уравнение и есть дифференциальное уравнение свободных затухающих колебаний пружинного маятника. Его, однако, принято записывать в следующем, так называемомканоническом виде:

   - коэффициент затухания,     - собственная частота свободных (незатухающих) колебаний пружинного маятника.

4. Коэффицент затухания - скорость затухания колебаний системы.

Декремент затухания 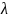 - количественная характеристика быстроты затухания колебаний в линейной системе; представляет собой натуральный логарифм отношения двух последующих максимальных отклонений колеблющейся величины в одну и ту же сторону.

,

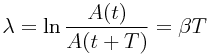где А – амплитуда колебаний, м

T – период колебаний, с

t – время колебаний, с

Методическая часть:

Рисунок 1 Пружинный маятник.

Если окружность имеет радиус 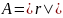, а угловая скорость вращения точки постоянна, то проекция:

Период изменения x, очевидно, будет равен T=2π/ω, где T – время одного оборота

точки, через которое весь процесс в точности повторяется; ω – циклическая (круго-

вая) частота; ϕo – начальный угол поворота относительно оси x. Следовательно,

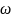
отличается множителем 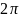от частоты ν:

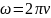
Так как максимальное значение косинуса равно единице, то максимальное значение x равно A. Это максимальное значение называется амплитудой колебаний. Аргумент косинуса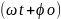 носит название фазы колебаний, а ϕo – начальной фазы колебаний.

Пусть теперь гармонические колебания вдоль оси x совершает материальная точка массой m. Выясним какая при этих условиях на нее должна действовать сила. Проекция скорости точки на ось x:

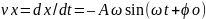
проекция ускорения:

.

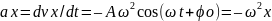По второму закону Ньютона:

,

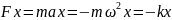Таким образом, для того чтобы материальная точка совершала гармонические ко-

лебания, действующая на нее сила должна быть пропорциональна x и направлена в

сторону, противоположную смещению x. Такая сила называется упругой.

Рассмотрим систему, состоящую из груза массой m, подвешенного на пружине, массой которой можно пренебречь. Пусть lo – длина пружины без подвешенного к ней груза, тогда под тяжестью груза пружина растянется на . В положении равновесия модуль силы тяжести 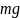равен модулю упругой силы :

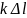, (1)

где k – коэффициент упругости пружины.

Коэффициент k численно равен силе, которую нужно приложить к пружине при упругой деформации, чтобы растянуть (или сжать) пружину на единицу длины. Если вывести груз из положения равновесия 0, то на груз будет действовать дополнительная сила упругости, проекция которой на направленную вниз ось x будет равна F = – kx (закон Гука). Под действием этой силы груз, после смещения на x = A и предоставленный самому себе, будет совершать гармонические колебания. Основное уравнение динамики поступательного движения (второй закон Ньютона) для груза принимает вид:

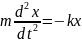(2)

Решение этого уравнения имеет вид:

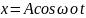(3)

Функция (3) – это закон движения груза на пружине, где A – амплитуда колебания,

т.е. наибольшее отклонение груза от положения равновесия.

Подставляя решение (3) в (2), получаем

Отсюда собственная частота системы

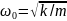
Так как , то

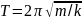(4)

В рассмотренном примере не учитывалась сила сопротивления, поэтому колебания считались незатухающими.