1. Требоания к выбираемому варианту структуры задаются в виде некоторых граничных значений для каждого показателя ( ).

Вариант считается лучшим и выбирается, если капитальные затраты на его создания не превосходят значения эксплуатационные затраты - оперативность -

надежность – . При этом вариант, удовлетворяющий всем требованиям, обычно не является единственным и принадлежит некоторому множеству допустимых вариантов Ω ( ). Очевидно, если требования к варианту предъявлены слишком жесткие, Ω=Ø. Рассмотренный подход является наиболее распространенным и широко используется в настоящее время при проектировании систем. Обычно выбирается некоторый один вариант, принадлежащий Ω. Если учесть, что Ω может содержать до нескольких тысяч вариантов, то становится ясно, что при таком подходе могут быть пропущены варианты, принадлежащие Ω и имеющие по ряду или даже по всем показателям лучшие значения, чем у выбранного варианта. Это является основным недостатком рассмотренного подхода.

2. Рассмотрим варианты, принадлежащие ω. Введем понятие сравнимых вариантов. Варианты 1 и 2 считаются сравнимыми, если

либо

Очевидно, если хотя бы одно неравенство выполняется строго, то худший вариант может быть отброшен, так как другой имеет по крайней мере по одному показателю лучшие значения при равных значениях по остальным. Проведя попарное сравнение вариантов из Ω и отбрасывая заведомо худшие, получаем множество Π попарно несравнимых вариантов или вариантов, оптимальных по Парето. Очевидно, Π Ω. Дальнейшее выделение лучшего варианта из Π сводится к выбору некоторой схемы компромисса, которая явно или неявно учитывает предпочтение одних показателей перед другими. Причем в зависимости от выбранной схемы компромисса лучшим вариантом может быть признан любой из Π. Если схема компромисса основывается на явном предпочтении одних показателей перед другими, то приходим к модели математического программирования (подход 3).

3.Предположим, что выбрана некоторая функция F, зависящая от показателей K, C, T, R, P и определяющая некоторую схему компромисса. Функция F(K, C, T, R, P) имеет смысл обобщенного критерия, учитывающего важность каждого показателя. В этом случае задача выбора лучшего варианта сводится к следующей задача математического программирования:

extr F(K, C, T, R, P) (3-25)

{Π}

Выбор схемы компромисса (выбор функции F) позволяет учесть желания и стремления разработчиков системы. Однако он остается творческим процессом, при котором могут быть допущены ошибки. Неудачный выбор функции F в сочетании с недостаточно точной информацией о показателях вариантов может в значительной степени уменьшить эффективность оптимизации. Этот недостаток может быть устранен путем отказа от полной формализации процесса выбора лучшего варианта. Предполагается следующий подход к решению задачи. Зададим схему компромисса (функцию F), наиболее полно отвечающую стремлению разработчика к назначению будущей системы. Пусть = extr F(K, C, T, R, P). Определим множество близких {Π} вариантов с точки зрения принятой схему компромисса D(F). Вариант принадлежит D(F), если значение обобщенного критерия F варианта лежит в интервале [ -δ, ]. Можно ограничить множество D(F) и по числу входящих в него вариантов. Ясно, что множество D Π. Задача состоит в поиске множества D. Очевидно, что при δ=0 она сводится к экстремальной задаче (3-25), которая является ее частным случаем.

Множество D должно состоять из небольшого числа вариантов, например из 10 вариантов, включая оптимальный (3-25). Окончательный выбор варианта, по которому будет построена система управления, остается за главным конструктором или комиссией экспертов. При этом могут быть учтены дополнительные факторы, неформализуемые в рамках математической модели.

Математическая модель задачи выбора варианта КУ основывается на следующих положениях.

Контур управления представляет собой цепочку последовательно выполняемых операций или задач управления (i= ). Каждая из задач может быть реализована на основе некоторых КУ принципов (алгоритмов). Выбор принципа реализации задачи определяет необходимый набор технических средств l= . Возможен случай, когда одно и то же техническое средство служит для выполнения нескольких различных операций, при этом его стоимость должна быть учтена только один раз.

Каждая задача управления должна выполняться в одном из узлов системы (j= ). При этом необходимо учитывать затраты на создание и эксплуатацию каналов связи между узлами, а также время передачи информации между последовательно выполняемыми задачами.

Для формализации задачи введем следующие переменные:

Каждый вариант построения контура должен включать в себя лишь один способ распределения задач по узлам системы и один принцип выполнения каждой задачи. Это учитывается следующим ограничением:

, i= (3-26)

Очевидно, множество значений переменной , удовлетворяющих ограничению (3-26), задает некоторый вариант построения КУ.

Переменные и зависят от и служат для удобства записи аналитических выражений расчета различных показателей качества вариантов КУ.

Используя обозначения, приведенные в табл. 3-2, характеристики любого варианта КУ можно выразить следующими формулами, где капитальные затраты К включают в себя стоимость технических средств в узлах системы ( ), стоимость создания каналов связи между узлами системы ( ), затраты на разработку алгоритмов и процедур выполнения задач ( ):

+ +

Таблица 3-2

Обозначение	Наименование
	Стоимость серийного технического средства l либо затраты на разработку и изготовление перспективных средств
	Стоимость создания канала связи включает стоимость технических средств приема и передачи информации между узлами j и j’
	Затраты на разработку информационного и математического обеспечения решения i-й задачи в k-м варианте в j-м узле
	Эксплуатационные затраты на решение i-й задачи в k-м варианте в j-м узле
	Затраты на передачу информации от i-й задачи, решаемой в j-м узле, к (i+1)-й задаче, решаемой в( j+1)-м узле
	Время решения i-й задачи k-м способом в j-м узле
	Время передачи информации от ij к (i+1), j’
	Надежность решения задачи (технического средства)
	Надежность передачи информации (канала связи)
	Масса технического средства l

Эксплуатационные расходы (С) состоят из эксплуатационных расходов на выполнение каждой задачи управления и затрат на передачу информации между различными узлами системы в процессе ее функционирования

Время выполнения цикла, характеризующее оперативность управления, вычисляется аналогично:

Надежность системы равна произведению показателей надежности элементов, входящих в последовательную цепочку, и после логарифмирования имеет следующий вид:

Масса приборов на борту ЛА:

Множество допустимых вариантов построения КУ, удовлетворяющих поставленным требованиям, задается с помощью системы неравенств:

Исходная оптимизационная задача выбора структуры типового КУ, минимальной по затратам на ее создание и эксплуатацию (3-25), может быть записана следующим образом:

(3-27)

при ограничениях

(3-28)

(3-29)

(3-30)

(3-31)

Сформулированная задача (3-27)-(3-31) является частным случаем обобщенной квадратичной задачи о назначениях с фиксированными доплатами, рассмотренной в [3-3].

Запишем эту задачу в более общем виде:

(3-32)

(3-33)

(3-34)

(3-35)

где функция имеет следующий вид:

В задаче (3-32)-(3-35) учитывается показателей качества функционирования системы.

Для построения эффективного алгоритма решения задачи перейдем от матричной модели (3-27) – ( 3-31) к сетевой.

Рассмотрим сетевой граф (рис. 3-2). Множество вершин графа состоит из непересекающихся подмножеств ( = ). Множества соответствуют различным вариантам реализации -ой задачи ( ) в различных узлах системы ( = ) и упорядочены

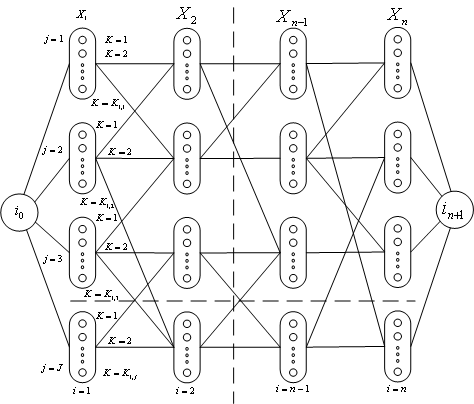
Рис. 3-2.

в соответствии со схемой выполнения задач КУ. Отображение Г задается матрицей смежности вершин графа

Причем смежными являются лишь вершины, принадлежащие множествам и =( ). Вершины принадлежащие одному и тому же множеству , не смежены.

Рассмотрим произвольный путь , связывающий миноранту графа с его мажорантой . Очевидно, является простым путем фиксированной длины и включает в себя кроме и еще вершин – по одной из каждого множества ( = ). Так как ограничение (3-26) выполняется автоматически, каждый такой путь соответствует некоторому варианту построения КУ (для каждой задачи выбраны вариант ее решения и узел ). И наоборот, каждому варианту построения КУ поставлен в соответствии единственный путь . Таким образом задача выбора оптимального варианта построения КУ эквивалентна задаче выбора экстремального пути на построенном сетевом графе .

Будем говорить, что на графе задана функция, если каждому простому пути , соединяющему вершины и , соответствует некоторое число , называемое обобщенной длиной пути .

Рассмотрим функции на графе, задаваемые выражением (3-36), в которых первая и вторая суммы соответствуют сумме весов вершин ( ) и дуг ( ) по показателю , входящих в . Эту часть будем обозначать .

Задача (3-32)-(3-35) в сетевых терминах формулируется следующим образом: найти путь на графе , имеющий минимальную длину при и ограниченные длины при .

Введем понятие прямого и обратного потенциалов вершин графа . Прямым потенциалом вершины относительно вершины и функции будем называть величину . Обратным потенциалом вершины относительно вершины и функции будем называть величину . Тогда для прямого и обратного потенциалов справедливы следующие свойства:

Свойство 1. , оно непосредственно следует из определения прямого и обратного потенциалов.

Свойство 2. , так как длина минимального пути, связывающего вершины и , не может быть больше суммы длин его частей для рассматриваемых .

Свойство 3. , так как при замене на .

115

122-125

мый программой при полном объеме исходных данных не превышает 160 Кбайт. Время счета на ЭВМ третьего поколения для размерности в 500 переменных не превышает 10 мин, а для размерности в 1500 переменных – 60 мин. Отметим, что большинство практических задач

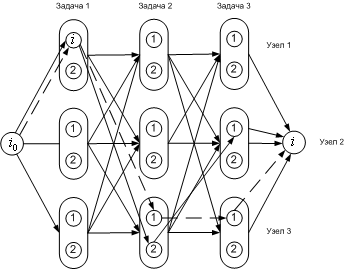
Рис. 3-4.

имеет размерность, не превышающую 1000 переменных. Исходная информация и результат решения выдаются на ЭВМ в виде табл. 3-3 – 3-7 рассматриваемого ниже примера [3-5].