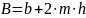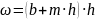2.1.2. Определение критической глубины

Критической глубиной h_к называется глубина, отвечающая минимуму удельной энергии сечения [1].

Если задано поперечное сечение русла, а также расход Q₀, то критическая глубина определяется из уравнения:

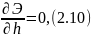
где Э – удельная энергия сечения, м, определяемая по формуле:

Для дорожно-мостового и аэродромного строительства при движении жидкости в каналах коэффициент Кориолиса принимают α =1,1.

Дифференцируя выражение (2.11) по h из условия при глубине, равной критической, получаем уравнение критического состояния потока:

где g – ускорение свободного падения, м/с²; ω_k – площадь живого сечения при критической глубине, м²; ширина канала поверху при критической глубине, м (рис. 2.3).

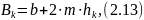
B_k

h_k

b

Рис. 2.3 Поперечное сечение подводящего канала

Для определения критической глубины буду использовать метод подбора.

Расчёт

1) из уравнения критического состояния потока при заданном расходе Q₀ определю числовое значение величины;

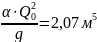
2) задавая числовые значения произвольно выбранным глубинам, вычислю соответствующие значения 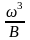. Для удобства расчёт сведу в таблицу 2.2.

Таблица 2.2. Определение критической глубины.

0,5	1,85	5,2	1,22
0,6	2,40	5,8	2,38
0,7	3,01	6,4	4,26

3) построю кривую =f(h). Масштаб для построения графика выбираю следующий: для оси глубин в 1 см по вертикали вкладывается 0,1 м (1:10), для оси ‒ масштаб произвольный (рис 2.4)

Рис. 2.4. График к определению h_k методом подбора.

Из графика видно, что при , .

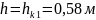В качестве второго метода применю графический метод.

Удельную энергию протекающей жидкости в соответствии с уравнением Бернулли можно определить относительно произвольной плоскости сравнения. Обозначив удельную энергию сечения через Э, запишем трехчлен Бернулли:

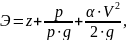
В открытых руслах для любой точки в потоке:

т. е. величина удельной потенциальной энергии равна глубине воды в сечении.

Тогда:

Таким образом, удельная энергия сечения складывается из удельной потенциальной энергии и удельной кинетической энергии 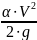. С учетом выражения средней скорости движения через расход ,

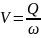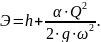
Из этого уравнения видно, что даже при постоянном расходе Q удельная энергия сечения при неравномерном движении меняется с изменением глубины потока h и, соответственно, площади живого сечения ω. Характер зависимости, определяемый уравнением 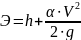, приведен на графике рис. 2.5

1) Задаюсь числовыми значениями произвольно выбранных глубин и вычислю соответствующие расходные характеристики.

Для удобства расчёт сведу в таблицу 2.3.

Таблица 2.3. Определение удельной энергии сечения.

			Э
0,40	1,36	0,56	0, 96
0,50	1,85	0,30	0,80
0,60	2,40	0,18	0,78
0,70	3,01	0,11	0,81
0,80	3,68	0,08	0,88

2) Построю кривую . Масштаб для построения графика выбираю следующий: для оси глубин в 1 см по вертикали вкладывается 0,1 м (1:10), для оси удельной энергии масштаб произвольный (рис. 2.5)

Рис. 2.5. График к определению h_k графическим способом.

Из графика видно, что минимальному значению удельной энергии сечения соответствует .

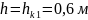В расчет принимаю .