1.4 Эффективный коэффициент теплоотдачи

2 Постановка задачи

2.1 Физическая постановка задачи

Область исследования – стенка сталеразливочного ковша, состоящая из футеровки и кожуха. Футеровка ковша состоит из двух слоев: рабочего толщиной 0,2м и арматурного толщиной 0,1м, выполненного из шамотного кирпича.

Рабочий слой представляет собой набивную футеровку, состоящую из муллитокорунда марки ММК-65 содержащего 65% Al₂O₃.

Передачу тепла через футеровку ковша следует рассматривать как нестационарный процесс теплопроводности через два слоя с различными теплофизическими свойствами.

Таблица 1

Теплофизические свойства муллитокорунда и шамотного кирпича

№ п/п	Наименование слоя	Теплофизические свойства
		Коэффициент температуропроводности а,м2/с	Плотность ,кг/м3	Удельная теплоемкость Ср, кДж/(кг К)	Коэффициент теплопроводности , Вт/(м К)
1	Рабочий	2,7·10-7	2360	1,10	0,68
2	Арматурный	6,74·10-7	2000	1.00	0,413

При выборе краевых условий необходимо исходить из следующего:

1. нестационарную теплопроводность в футеровке следует рассматривать как периодический процесс;

2. температура металла в ковше от выпуска из конвертера до окончания разливки непрерывно изменяется;

3. перед подачей нового ковша под выпуск металла, последний проходит операцию сушки и прогрева футеровки в результате чего в огнеупорных слоях устанавливается определенное начальное распределение температуры;

4. потери тепла с поверхности кожуха ковша в окружающую среду зависят от его температуры и являются переменной величиной по ходу компании его эксплуатации.

Поэтому для определения краевых условий были проведены дополнительные исследования.

В процессе футеровки ковша в различных точках арматурного и рабочего слоев были вмонтированы термопары, с помощью которых были определены температурные поля в соответствующих слоях перед подачей ковша под выпуск металла из конвертера (начальные условия).

2.2. Математическая модель.

Сформулируем математическую модель задачи о теплопотерях в стенке на примере сталеразливочного ковша, учитывая следующие предположения:

1. Даны габаритные размеры ковша и стенки: высота Н=4,3м; внутренний и внешний диаметры ковша d₁=4,2м и d₂=4,4м.; толщина стенки стенки, где 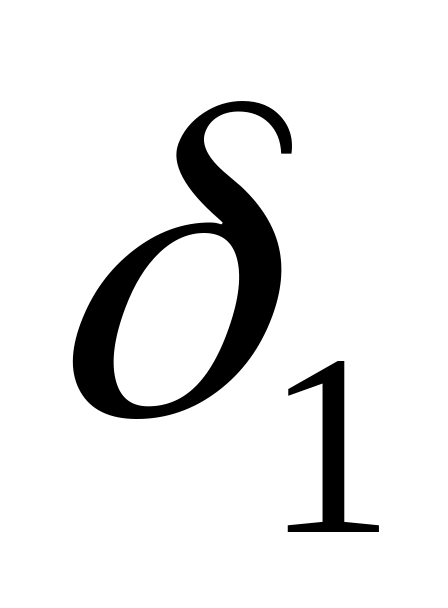– толщина рабочего слоя, 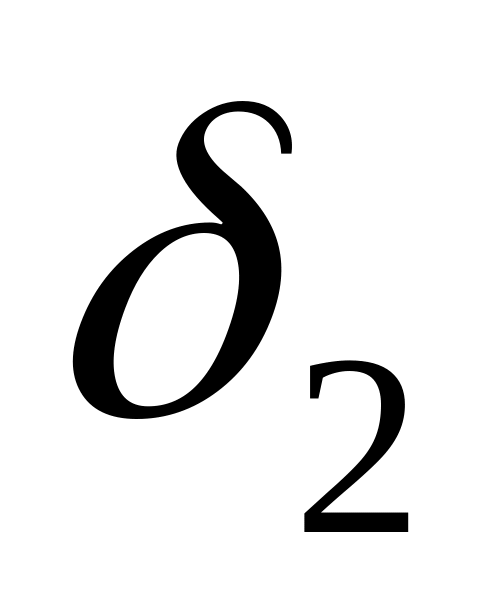– толщина арматурного слоя.

2. Термическим сопротивлением металлического кожуха принебрегаем, т.к. его толщина значительно меньше толщины футеровки, полагая t_кож.=t_2.

3. Между слоями стенки обеспечен идеальный тепловой контакт.

4. Материалы рабочего и арматурного слоев имеют следующие теплофизические свойства, приведенные в таблице 1.

5. Распростронение теплового потока в продольных направлениях стенки не учитываем в связи с однородностью режимов подвода тепла на границе контакта с металлом и теплосъема на внешней поверхности кожуха для всего ковша.

6. Кривизной стенки ковша принебрегаем, т.к. толщина стенки значительно меньше ее габаритных размеров.

В следствии того, что работа сталеразливочного ковша состоит из двух периодов, наша задача разобъется на две части: первая будет описывать процесс нагрева футеровки, определяемая временем пребывания металла в ковше ( ), где начальными условиями будут являться распределения температуры, полученные эксперементально; вторая часть будет описывать процесс охлаждения футеровки, время от окончания разливки до подачи ковша к последующему выпуску металла из конвертера ( ), для которой начальным условием будет являтся конечное распределение температуры из первой части.

Данный процесс можно описать системой дифференциальных уравнений в частных производных:

; (1)

, (2) где и - текущие температуры в соответствующих слоях, С; и - соответственно коэффициенты температуропроводности в слоях, м²/с; -текущее время, С; - текущая координата, м.

Для решения поставленной задачи уравнения (1) и (2) необходимо дополнить начальными и граничными условиями. Если принять границу раздела металл- наружная поверхность рабочего слоя за начало координат (рис.3), то исходные уравнения (1) и (2) можно дополнить следующими краевыми условиями:

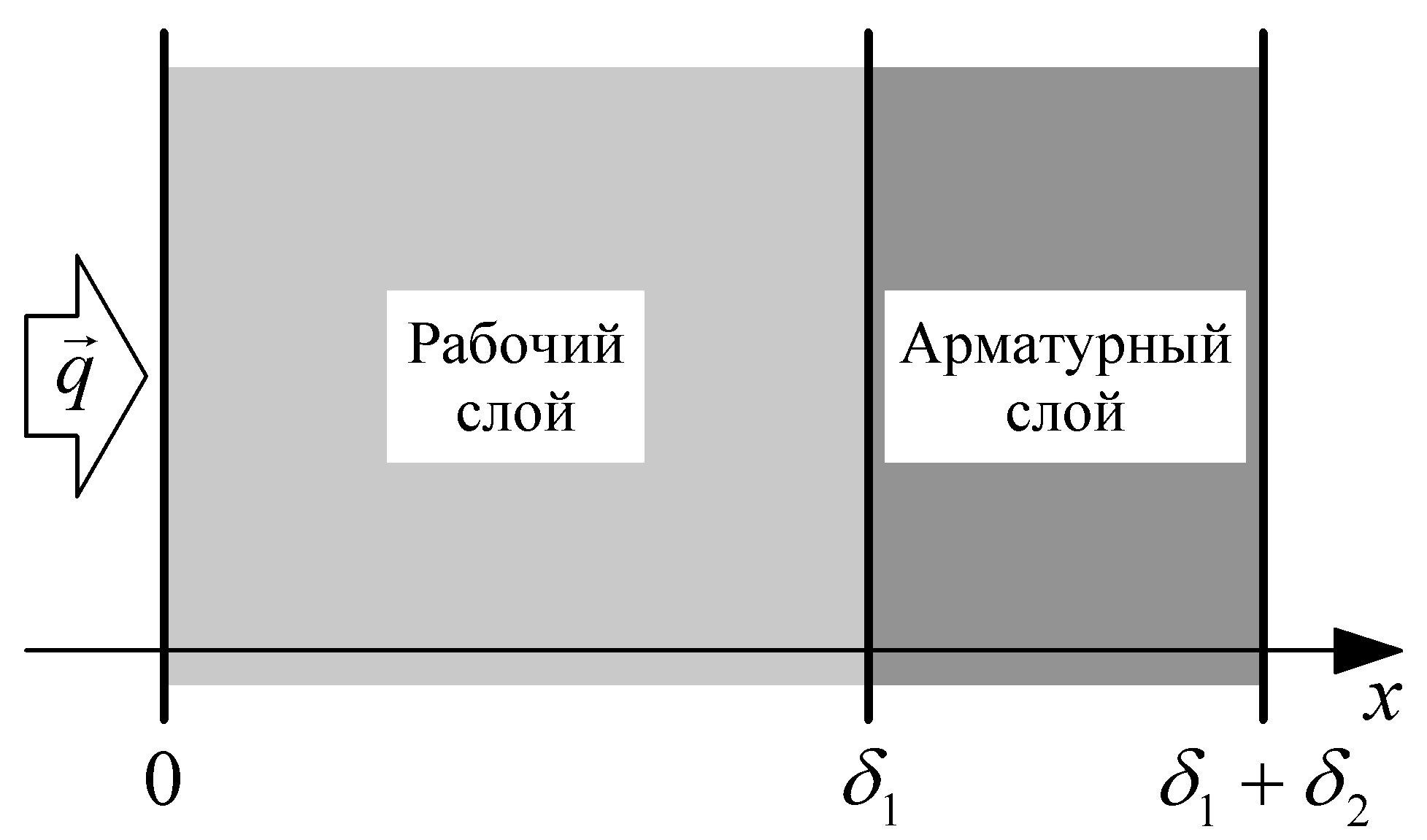
Рисунок 3. Схема распределение тепла в двухслойной футеровке ковша: ₁ – толщина рабочего слоя; ₂ – толщина арматурного слоя.

для первой подзадачи

Начальные условия:

На рис. 1 представлены температурные поля в арматурном и рабочем слоях, полученных на основе экспериментальных замеров

В момент времени для рабочего и арматурного слоев должны выполнятся следующие распределения температур :

(3)

(4)

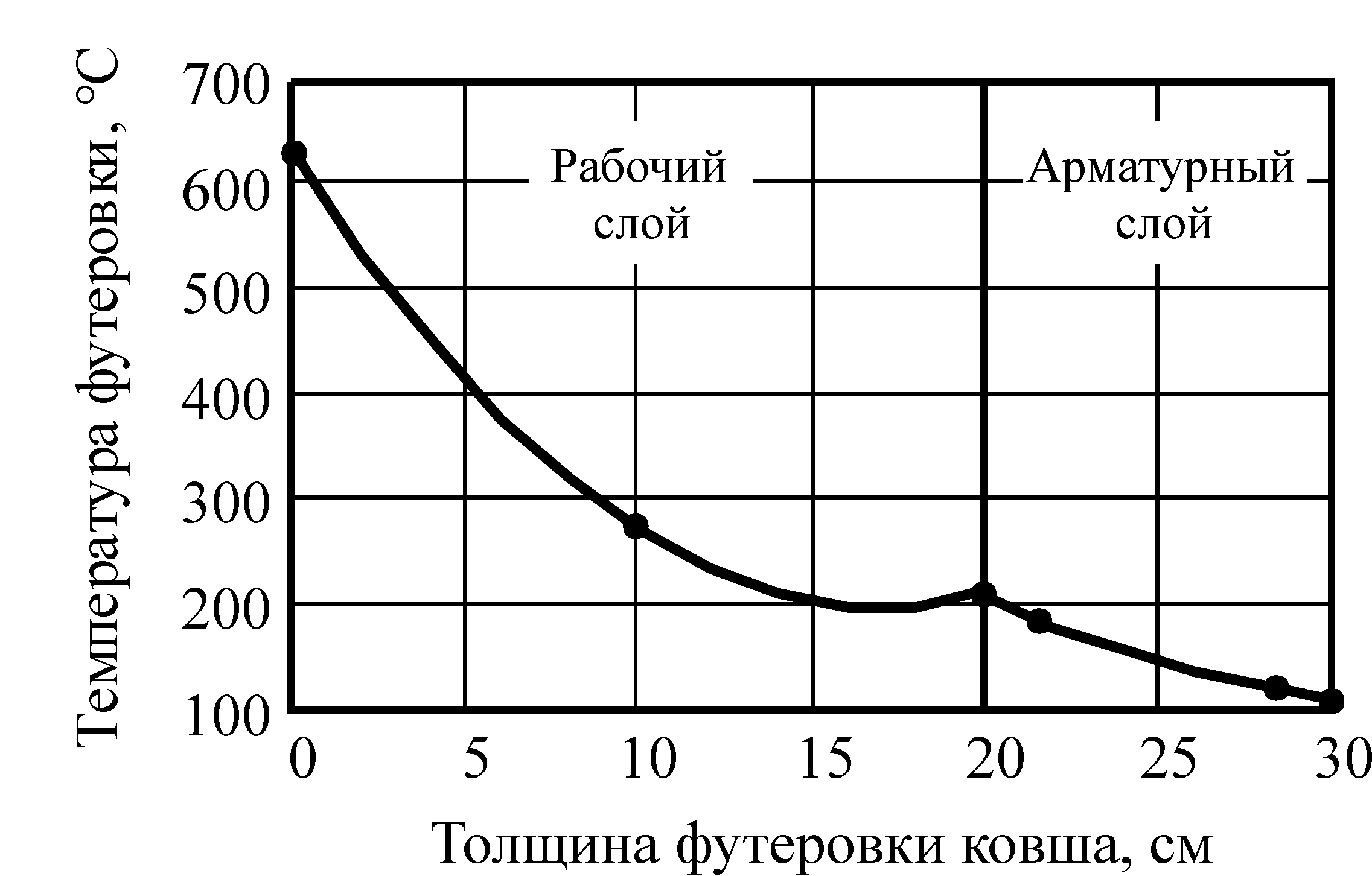
Рисунок 1. Распределение температуры в рабочем и арматурном слое футеровки после стенда подогрева ковша.

Граничные условия:

При низкой теплопроводности рабочего слоя на его поверхности можно принять граничные условия первого рода, (задание температуры) т.е. при должно выполняться условие .

, (5)

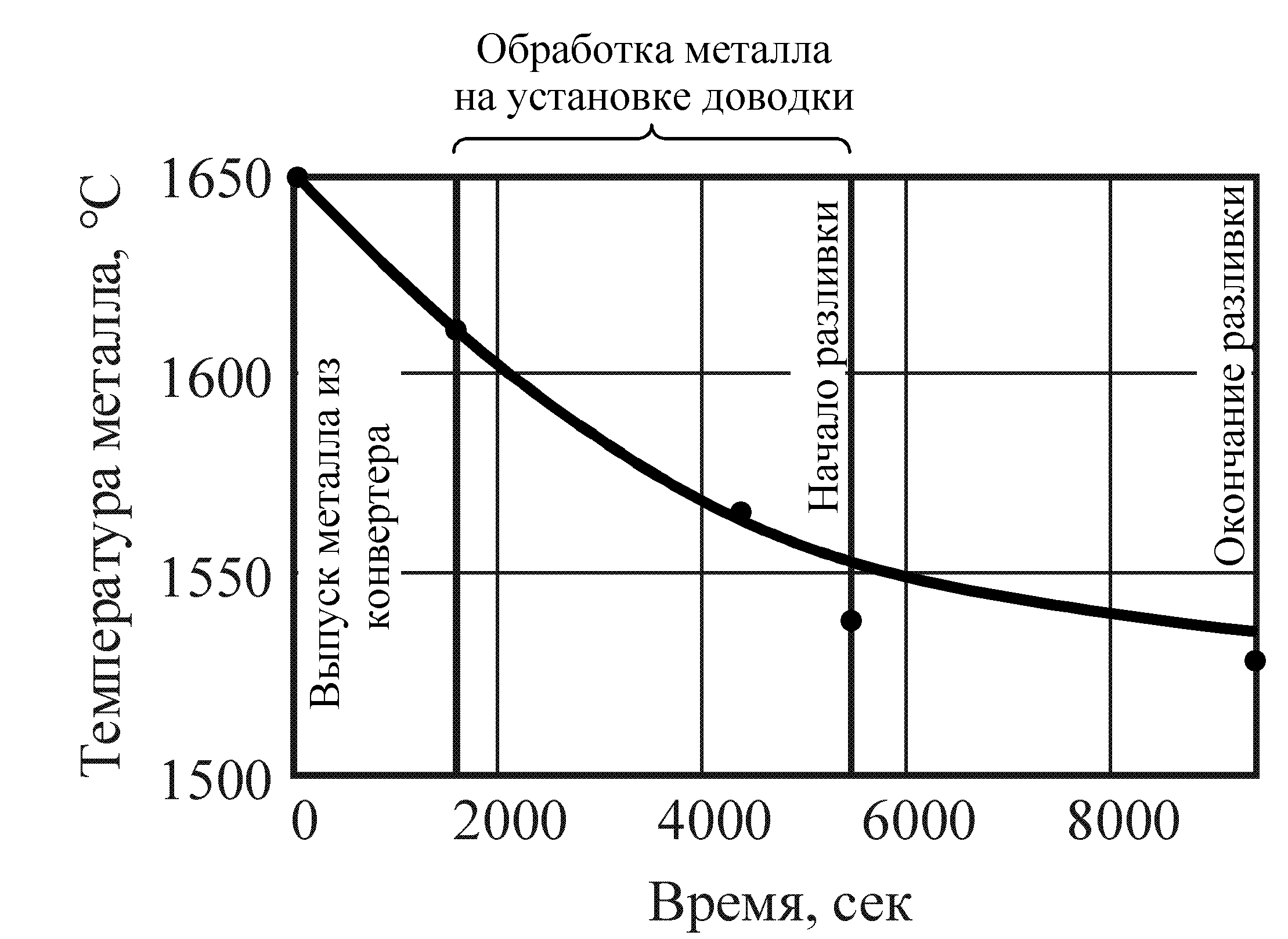
Рисунок 2. Изменение температуры метала в ковше.

Исключая термическое сопротивление на границе рабочего и арматурного слоев можно составить следующее условие (граничное условие четвертого рода), а именно:

При _, (10) где и - соответственно коэффициенты теплопроводности рабочего и арматурного слоев, Вт/м К.

Условие (10) необходимо дополнить еще одним условием:

(11)

На рис.2 показано изменение температуры металла за время его пребывания в ковше (до окончания разливки), полученное на основе обработки экспериментальных данных. Кривая, представленная на рис.2, аппроксимируется эмпирическим уравнением:

Потери тепла через футеровку ковша в окружающую среду определяли по уравнению:

, (6)

где - плотность теплового потока в окружающую среду, Вт/м²;

- коэффициент теплоотдачи от поверхности кожуха в воздушную среду, Вт/м²К;

- температура кожуха ковша, С;

- температура окружающей среды, С.

При свободном движении воздуха вдоль вертикальной поверхности кожуха ковша для турбулентного режима коэффициент теплоотдачи ( ) определяется из критериального уравнения [2]:

, (7) где - критерий Нуссельта;

- критерий Грасгофа;

- критерий Прандтля.

В выражениях для , и приняты следующие обозначения:

Н- высота ковша;

, , , - соответственно коэффициенты теплопроводности, температуропроводности, кинетической вязкости и объемного расширения воздуха.

Принимая температуру воздуха в цех и определив значения , , , находим коэффициент теплоотдачи при свободной конвекции по формуле:

(8)

Если пренебречь термическим сопротивлением металлического кожуха ( ) с учетом (8) удельный тепловой поток от поверхности кожуха в окружающую среду будет равен:

(9)

Поэтому при должно выполняться условие:

(12)

Для второй подзадачи.

Начальные условия

Для периода охлаждения ковша начальными условиями является распределение температуры в рабочем и арматурном слоях, полученное в конце периода нагрева.

Граничные условия для второй подзадачи отличаются от первой формулировкой условия на внутренней стороне футеровки.

Для определения граничных условий периода охлаждения ковша с помощью оптического пирометра были проведены замеры температуры внутренней поверхности футеровки в зависимости от времени его охлаждения (рис.4).

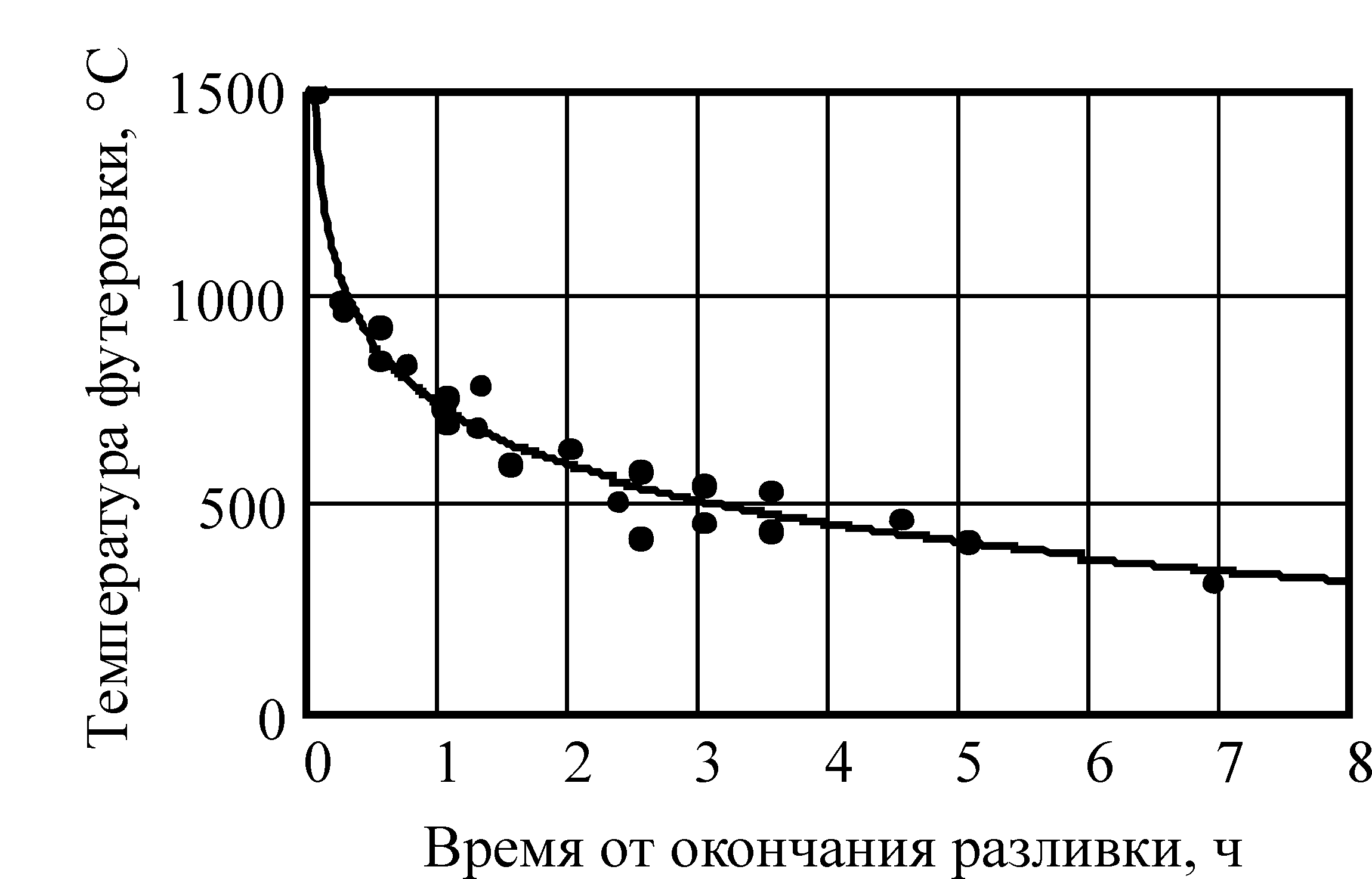
Рисунок 4. Изменение температуры внутренней поверхности футеровки в процессе охлаждения ковша.

В соответствии с данными замеров зависимость температуры поверхности рабочего слоя от продолжительностью охлаждения ковша ( ) удовлетворительно описывается эмпирическим уравнением:

(13)

При и должны выполняться условия (10-12).

2.3 методика оценки тепловых потерь