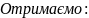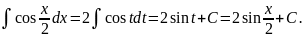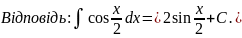НЕВИЗНАЧЕНИЙ ІНТЕГРАЛ

1.Поняття невизначеного інтегралу.

Диференціювання – це дія, з допомогою якої за даною функцією знаходять похідну чи диференціал цієї функції.

Знаходження похідної має велике практичне значення. Так, за відомим законом руху тіла S=S(t) ми диференціюванням знаходимо швидкість ν(t)=S`(t), а пізніше і прискорення a(t)=S''(t); якщо задано рівняння прямої y=ƒ(x), то легко визначити кутовий коефіцієнт дотичної, проведеної до даної кривої: k=ƒ'(x).

Важливими є і оберненні задачі, наприклад:

а) відома швидкість руху тіла, встановити закон його руху.

б) дано кутовий коефіцієнт дотичної до кривої, знайти рівняння цієї кривої.

Інакше кажучи, за даною похідною треба знайти функцію, від якої знайдена ця похідна, тобто виконати дію обернену диференціюванню. цю дію називають інтегруванням. З допомогою інтегрування за даною похідною або диференціалом функції знаходять саму функцію, яку називають первісною.

Диференційована функція F(x) називається первісною для функції ƒ(x) на проміжку a<x<b, якщо F'(x)= ƒ(x) для кожного a<x<b.

Так, для функції ƒ(x)=cosx первісною є функція F(x)=sinx, оскільки (sinx)'=cosx. Зауважимо, що дана функція має не єдину первістну. Наприклад, функції F₁(x)=sinx+1, F₂(x)=sinx+3, F₃(x)=sinx-4, які відрізняються лише на постійну, теж задовольняють умову F₁(x)=cosx.

Доведемо теорему: якщо F(x) – первісна для ƒ(x) на деякому проміжку, то і функція F(x)+С, де C – будь-яка постійна, також є первісною для функції ƒ(x) на цьому проміжку.

Доведення:

(F(x)+С)'= F'(x)+С'=ƒ(x).

Отже, досить знайти для функції ƒ(x) тільки одну первісну функцію F(x), щоб знайти всі її первісні, бо вони відрізняються одна від одної тільки на одну первісну величину C.

Сукупність F(x)+С всіх первісних функції ƒ(x) на інтервалі a<x<b називають невизначеним інтервалом від функції ƒ(x) а цьому інтервалі і позначають .

Тут - підінтегральний вираз, 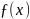– підінтегральна функція, 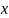- змінна

Наприклад: +C, бо (tgx+C)' =

Геометрично F(x)+С можна зобразити як сімейство кривих, отриманих паралельним переносом будь-якої з них вздовж осі OY(рис. 1).

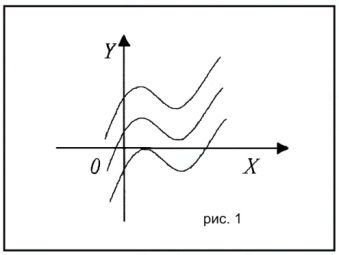
Якщо функція ƒ(x) має на деякому проміжку хоч одну первісну, то її називають інтегрованою на цьому проміжку.

2. Властивості невизначеного інтегралу.

1. Похідна невизначеного інтегралу рівна підінтегральній функції; диференціал невизначеного інтегралу рівний підінтегральному виразу:

2. Невизначений інтеграл від диференціалу функції рівний цій функції:

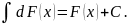
3. Постійний множник можна винести за знак інтегралу:

4. Невизначений інтеграл від алгебраїчної суми функції рівний такій самій алгебраїчній сумі невизначених інтегралів від кожної функції:

5. Якщо функція F(x) є первісною для ƒ(x), де k і b довільні числа (k≠0), то

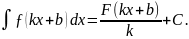
Для доведення властивостей 1-5 достатньо знайти похідні обох частин рівності.

Наприклад, доведемо властивість 4:

і похідна лівої частини

буде тотожно рівна правій частині.

Основні формули інтегрування (таблиця інтегралів).

З кожної формули диференціювання випливає відповідна її формула інтегрування. Наприклад, з того, що , слідує рівність

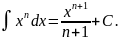
Запишемо таблицю основних інтегралів:

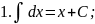
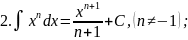
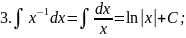
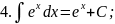
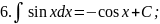
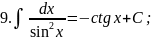
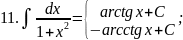
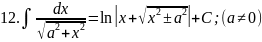
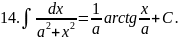
Справедливість цих формул легко перевірити диферен-ціюванням

3. Безпосереднє інтегрування.

Під безпосереднім інтегруванням розуміють такий спосіб знаходження інтегралу, коли шляхом тотожних перетворень підін-тегральної функції та застосування властивостей невизначеного інтегралу приходимо до одного чи декількох табличних інтегралів.

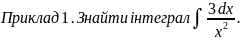
Розв’язування: Використовуємо властивості степеня з від’ємним показником (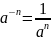 ; a>0) і знайдемо невизначений інтеграл від степеневої функції:

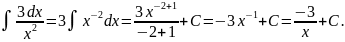
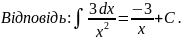
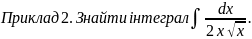
Розв’язання: Використаємо властивість степеня з дробовим показником 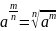і знайдемо невизначений інтеграл від сте-пеневої функції:

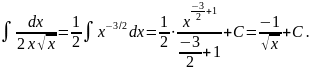
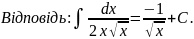
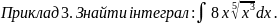
Розв’язання: Використаємо властивість степеня з дробовим показником і правило множення степеня з однаковими основами

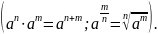
Знайдемо невизначений інтеграл від степеневої функції:

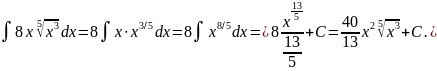
Розв’язання: Використаємо властивості степеня з дробовим показником, правила дій над степенями з однаковими основами і знайдемо інтеграл від кожного доданку окремо:

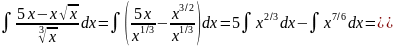
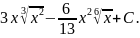
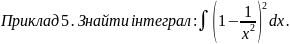
Розв’язання: Відкриємо дужки за формулою і невизначений інтеграл від отриманої алгебраїчної суми функції замінимо такою ж алгебраїчною сумою невизначених інтегралів від кожної функції:

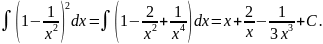
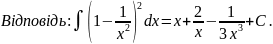
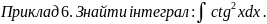
Розв’язання: Для знаходження інтегралу використаємо фор-мулу і властивості невизначеного інтегралу:

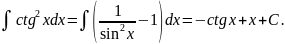
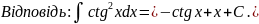
В практиці інтегрування часто зустрічаються інтеграли, для знаходження яких можна використовувати формули, які випливають з властивості 5:

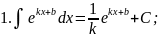
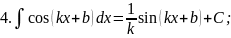
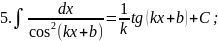
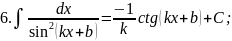
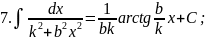
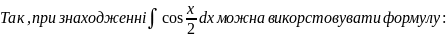
тоді

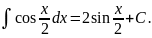
4. Інтегрування методом підстановки (заміна змінної).

Якщо інтеграл неможливо привести до табличного з допомо-гою елементарних перетворень, то одним з способів інтегрування є метод підстановки (заміни змінної).

Суть методу підстановки полягає в наступному: заміняють новою змінною таку частину підінтегральної функції, при диференціюванні якої отримуємо ту частину, що залишилась (не враховуючи постійного множника, на який завжди можна домножити чи доділити необхідний вираз). В результаті введення заміни підінтегральний вираз повинен набути вигляду:

ƒ(t(x))·t(x)dx=ƒ(t)dt,

що дозволяє звести інтеграл до табличного.

Розв’язання: Зробимо підстановку t=5-3x, тоді dt=-3dx,

Далі:

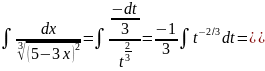
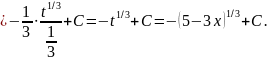
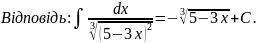
Приклад 8. Знайти інтеграл:

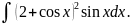
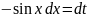Розв’язання: Нехай , тоді: , звідки

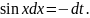
Отримаємо:

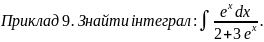
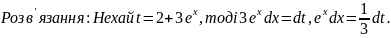
Далі отримаємо: