44. Криволинейный интеграл 1 рода (определение, свойства)

f(M) непрерывна на дуге АВ. Δl_i=длина дуги каждой nой части дуги АВ. M_i=точка та каждой части дуги.

Интегральная сумма:

Таких интегральных сумм можно составить бесконечное множество, однако при неограниченном возрастании n и стремлению к нулю наибольших из длин частичных дуг, у всех интегральных сумм существует предел, который называется криволинейным интегралом по длине дуги или интеграл 1 рода.

∫f(M)dl

AB

45. Криволинейный интеграл 2 рода

Криволинейный интеграл 2-го рода (по координатам) называются интегралы АВ. 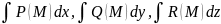. Они отличаются от интегралов 1-го рода тем что при составлении интеграла сумма берется не длина частичной дуги а её проекция на соответствующую координатную ось ∆ . Криволинейный интеграл 2-го рода обычно записывают в виде 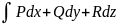. Если линия по которой вычисляется криволинейный интеграл замкнута то записывают символ Положительным считается обход по часовой стрелке иначе отрицательным 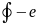и 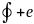. обыкновенный определенный интеграл это частный случай криволинейного интеграла для которого линией интегрирования является прямолинейный отрезок. Криволинейный интеграл 2-го рода обладает следующим свойством интеграл АВ=-интеграл АВ. Кривую по которой происходит интегрирование можно разбить по части интеграл АВ= интеграл АС + интеграл АВ. Обычно криволинейный интеграл вычисленный по различным линиям соединяющий 2 точки А и В имеет различное значения.

46. Теорема о независимости криволинейного интеграла от линии интегрирования.

Пусть в некоторой плоской, односвязной области D, выражения Pdx+Qdy является полным дифференциалом некоторой функции, тогда криволинейный интеграл по дуге АВ не зависит от линии интегрирования, соединяющей точки А и В и он равен нулю, если вычислен по любой замкнутой линии в области D.

Выражение Pdx+Qdy будет являться полным дифференциалом функции U(x,y) тогда и только тогда, когда P’y=Q’x