Формула Ньютона-Лейбница (доказательство теоремы)
Если
f(x)
непрерывная на отрезке [a,b],
то интеграл
,
где F(x)
– первообразная для f(x)
Доказательство:
Если функция непрерывна, то она интегрируема. Следовательно существует интеграл к тому же для f(x) существует первообразная Ф(х)=
Т.к. Ф(х) одна из первообразных, то Ф(х)=F(x)+c (любая первообразная F(x)).
Заметим,
что Ф(а)=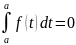
То есть, при x=a Ф(a)=F(a)+c, C=-F(a).
То
есть Ф(x)=F(x)-F(a).
При х=b
в этой формуле получаем Ф(b)=F(b)-F(a)
и Ф(b)=
Интеграл:
Теорема доказана!
Свойства определенного интеграла
Пусть все функции непрерывны на рассматриваемой промежутках.
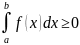из-за f(x)
геометрически это означает что S
криволинейной трапеции ограничена
сверху графиком неотрицательной
функции и есть неотрицательное число.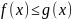
a,b
если функция не превосходит то и для
интегралов выполняется тоже
Интегрирование по частям в определенном интеграле: доказательство формулы
обозначим
неопределенный интеграл
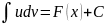а интеграл
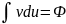(x)+
.
Так справедлива формула для неопределенного
интеграла
,
F(x)+
F(x)=u(x)v(x)-
+c.
Это равенство при х=б принимает вид
F(b)=u(b)v(b)-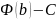
;
при х=а F(а)=u(а)v(а)-
.
Составим разность F(b)-F(a):
F(b)-F(a)=(u(b)v(b)-u(a)v(a))-(Ф(б)-Ф(а))
Теорема (замена переменной в определенном интеграле)
Теорема:
пусть функция y=f(x)
имеет произвольную на отрезке а,б а
функция x=ϕ(t)
определена на всем отрезке αβ а
дифференцируемая внутри по прежнему
ϕ(α)=а,
ϕ(β)=б
и отрезок ϕ
.
Тогда справедлива формула в определенном
интеграле:
Вычисление площадей плоских фигур (случай а) декартовые координаты)
Если
f(x)
0
на отрезке
то S
криволинейной трапеции ограниченной
кривой y=f(x)
и прямой x=a
x=b
y=0
.
Если
же f(x)≤0
на отрезке
то и сам интеграл
≤0 то
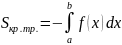
Пусть
теперь на отрезке а,б функция f(x)
меняет знак конечное
число раз.
В
этом случае интеграл по всему отрезку
разбивает на сумму интегралов по
частичным отрезкам и площадь равна
разност площадей лежащих выше оси Ох
и площадь лежащих ниже оси Ох
Вычисление площадей плоских фигур (случай б) параметрические уравнения)
Б) вычислим
площадь криволинейной трапеции
ограниченной кривой с заданными
параметрами уравнениями
где α
ϕ(α)=a
, ϕ(β)=b.
Параметрическое уравнение определяется
в некоторой функции y=f(x)
на отрезке а,б и её S=
.
В этом интервале сделаем замену
переменных x=ϕ(t)
тогда dx=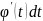
,
y=ψ(t).
S=
.
Длина дуги (случай а) декартовые координаты)
А) пусть
кривая задана в прямоугольных координатах
y=f(x)
тогда длина дуги а,б этой кривой
заключенной между прямыми х=а, х=а
вычисляется по
l=
.
Длина дуги (случай б) параметрические уравнения)
. Б) пусть
кривая задана параметрами уравнения
где α
ϕ,ψ
- непрерывная дифференцируемая
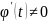
. Параметр уравнения определяет некоторую
кривую y=f(x),
которая непрерывная вместе со своей
производной. Для параметра с заданной
функцией производная равна
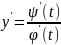ϕ(α)=a,
ϕ(β)=b.
Сделаем замену переменных в определенном
интеграле выражающим длину дуги. x=ϕ(t),
dx=
l=