18. Верхняя и нижняя суммы Дарбу

нижняя и верхняя сумма Дарбу.

= и =

– площадь ступенчатой фигуры составлен из прямоугольников вписанных в криволинейную трапецию. – площадь ступенчатой фигуры составленной из прямоугольника описанного около криволинейной трапеции.

19. Свойства сумм Дарбу

1) для любого разбиения ≤ .

2) если к 1 разбиению отрезка добавить несколько новых точек получив тем самым 2 разбита, то

Последние свойства означает что множество нижних сумм Дарбу расположена левее множества верхних сумм Дарбу следовательно найденные хотя бы одно число разделяющие эти два множества = .

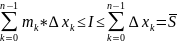20. Определение неопределенного интеграла

функция y=(f) ограниченная на отв. а,б называется интегрируемой на этом отрезке если существует число I разделяет множество верхних и нижних сумм Дарбу, составленных для всевозможного разбиения а,б это число называется определенным интегралом данной функции по отрезку а,б. а – нижний предел интеграла I= (a ); б – верхний предел интеграла =- (a если а=б ∆ .

21. Геометрический и физический смысл определенного интеграла

Рассмотрев криволинейную трапецию мы выяснили определенный геометрический смысл определенного интеграла . рассмотрим прямоугольник неоднородный стержень а,б линейная плоскость в точке х выражается функцией ∂(х) тогда масса стержня m=

22. Интегрирование по частям в определенном интеграле. Типы интегралов, берущихся по частям.

1 тип интегралов: f(x)-многочлен

2 тип интегралов:

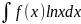
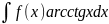
3 тип интегралов:

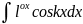
23. Теорема (аддитивность определенного интеграла)

Если функция интегрируема на отрезках ас сб где а то она интегрируема и на всем отрезке аб причем выполняется равенство S=

24. Теорема о среднем значении (доказательство)

Если f(x) непрерывна на отрезке а,б то существует точка С из отрезка а,б такая что . F(c)= среднее значение.

Доказательство: по теореме 2 из непрерывности функции следовательно её интегрируемость на отрезке обозначим m и M – наименьшей и наибольшей значение функции на отрезке а,б тогда выражение m(b-a) и M(b-a) является и Дарбу для разбиения отрезка который состоит из одной части самого отрезка.

тогда разделяющие число m(b-a) m . Таким образом между наименьшим и наибольшим значением непрерывной функции на отрезке лежит значение этой функции в некоторой (средней) точке ас отрезка а,б с ϵ а,б. ч.т.д.

Геометрический смысл этой теоремы площадь криволинейной трапеции равна площади прямоугольника имеющего тоже основание что и трапеция и высоту f(c).

25. Теорема о существовании первообразной для непрерывной ф-ии. Интеграл с переменным верхним пределом.

Если f(x) непрерывна на отрезке [a,b], то функция Ф(x)= , то функция дифференцируема в любой внутренней точке x (a,b),при этом Ф’(x)=f(x). То есть интеграл с переменными верхним пределом является одной из первообразной для непрерывного под интегрирования функции.