3.4.2. Проверочный расчет на контактную прочность при действии максимальной нагрузки:

(3.56)

где: - исходная расчетная нагрузка, в качестве которой принимается наибольший из действующих на шестерню вращающий момент в Нм, для которого число циклов перемен напряжений не менее . В данном случае ;

- наибольший вращающий момент на валу шестерни, Нм. В данном случае ;

- коэффициент, учитывающий динамическую нагрузку, возникающую в зацеплении до зоны резонанса.

- коэффициент, учитывающий динамическую нагрузку, возникающую в зацеплении при нагрузке :

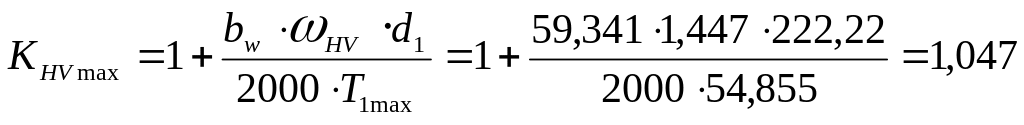(3.57)

где: - делительный диаметр шестерни, мм;

- ширина зубчатого венца колеса, мм;

- наибольший вращающий момент на валу шестерни, ;

- удельная окружная динамическая сила, Н/мм.

- допускаемое контактное напряжение при максимальной нагрузке, не вызывающее остаточных деформаций или хрупкого разрушения поверхностного слоя:

(3.58)

где: - предел текучести материала зубьев, МПа. Для Стали 40ХН

<1680МПа

Напряжения, полеченные при расчете от действия реальной нагрузки, возникающей в процессе работы, меньше допустимых.

3.4.3. Расчет зубьев на выносливость при изгибе, выполняется раздельно для колеса и шестерни:

(3.59)

- окружная сила на делительном цилиндре, Н:

(3.60)

где: - исходная расчетная нагрузка, в качестве которой принимается наибольший из действующих на шестерню вращающий момент в , для которого число циклов перемен напряжений более . В данном случае .

- делительный диаметр шестерни, мм.

- коэффициент, учитывающий влияние вида зубчатой передачи:

Вид передачи	Значение коэффициента
прямозубая	0,16
косозубая и шевронная	0,06

Таблица 3.5.

Так как передача прямозубая, то принимаем

- коэффициент, учитывающий влияние разности шагов зацепления зубьев шестерни и колеса, принемаем по таблице 3.3.

- удельная окружная динамическая сила, Н/мм:

(3.61)

где: - коэффициент, учитывающий влияние вида зубчатой передачи;

- коэффициент, учитывающий влияние разности шагов зацепления зубьев шестерни и колеса;

- окружная скорость, м/с;

- начальное межосевое расстояние, принятое для изготовления передачи, мм;

- передаточное отношение передачи.

Значение коэффициента

Модуль ,мм	Степень точности по нормам плавности по ГОСТ 1643–81
	5	6	7	8	9	10
до 3,5	85	160	240	380	700	1200
св. 3,5 до 10	105	194	310	410	880	1500
св. 10	150	250	450	590	1050	1800

Таблица 3.6.

Так как модуль менее 3,5 мм и выбранная степень точности - 8 , то

- коэффициент, учитывающий динамическую нагрузку, возникающую в зацеплении до зоны резонанса:

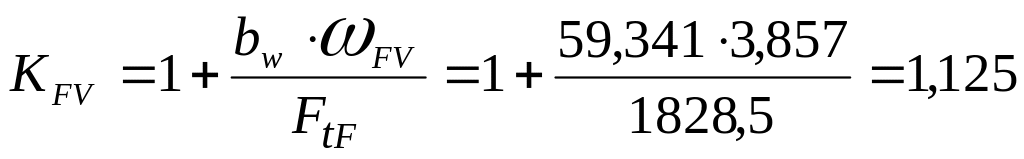(3.62)

где: - удельная окружная динамическая сила, Н/мм;

- окружная сила на делительном цилиндре, Н;

- ширина зубчатого венца колеса, мм.

- коэффициент, учитывающий неравномерность распределения нагрузки по длине контактных линий в начальный период работы передачи:

(3.63)

где: - делительный диаметр шестерни, мм;

при расположении шестерни на валу передачи со стороны подвода вращающего момента;

- ширина зубчатого венца колеса, мм.

- коэффициент, учитывающий неравномерность распределения нагрузки по длине контактных линий:

(3.64)

где: - коэффициент, учитывающий неравномерность распределения нагрузки по длине контактных линий в начальный период работы передачи.

Для прямозубой передачи: 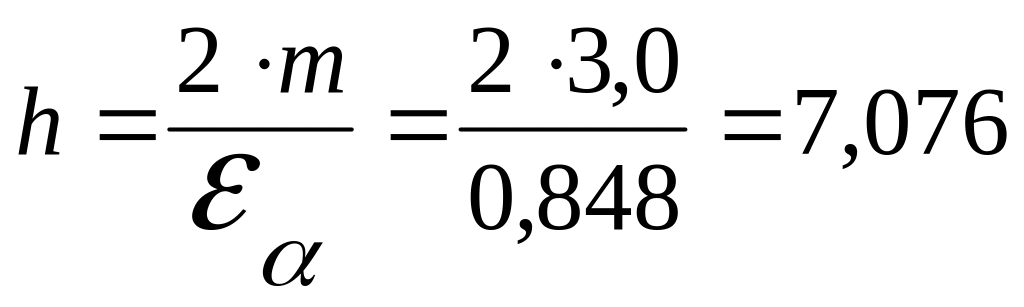(3.65)

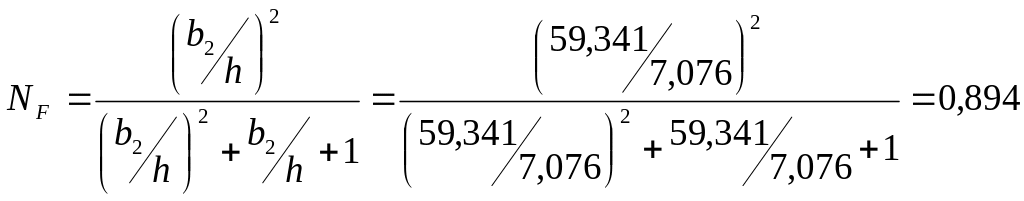(3.66)

- коэффициент, учитывающий распределение нагрузки между зубьями. Так как передача прямозубая, то принимаем .

- коэффициент, учитывающий форму зуба шестерни и концентрацию напряжений:

(3.67)

где: - коэффициент смещения исходного контура шестерни;

- эквивалентное число зубьев шестерни.

- коэффициент, учитывающий форму зуба колеса и концентрацию напряжений:

(3.68)

где: - коэффициент смещения исходного контура колеса;

- эквивалентное число зубьев колеса.

- коэффициент, учитывающий наклон зуба:

(3.69)

где: - коэффициент осевого перекрытия;

- угол наклона зубьев, град.

- коэффициент, учитывающий распределение нагрузки между зубьями. Так как передача прямозубая, то принимаем .

Подставляем полученные значения коэффициентов в формулу (2.59) и вычисляем напряжения раздельно для шестерни и колеса:

Полученные значения напряжения меньше допускаемых.