3.2.3. Ориентировочное значение модуля:
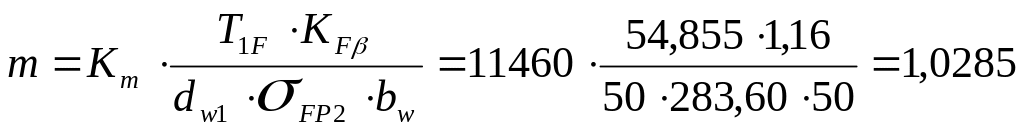(мм)
(3.20)
где:
- диаметр шестерни, мм;
-
ширина зубчатого венца колеса, мм;
-
допускаемые напряжения изгиба зубьев
колеса, МПа;
-
вспомогательный коэффициент; так как
передача прямозубая, то
;
-
коэффициент, учитывающий неравномерность
распределения нагрузки по длине
контактных линий. Значение
принимаем в зависимости от параметра
по графикам, используя рекомендация
Добровольского В.П. В данном случае
принимаем
;
-
исходная расчетная нагрузка, в качестве
которой принимается наибольший из
действующих на шестерню вращающий
момент в
,
для которого число циклов перемен
напряжений более
.
В данном случае
.
Полученная расчетная величина модуля предварительна. Окончательное значение выбираем из таблицы стандартных значений:
Модуль
,
мм, по ГОСТ 9563–60
1 ряд |
1,5 |
2,0 |
2,5 |
3,0 |
4,0 |
5,0 |
6,0 |
8,0 |
10,0 |
2 ряд |
1,75 |
2,25 |
2,75 |
3,5 |
4,5 |
5,5 |
7,0 |
9,0 |
|
Таблица 3.1.
Окончательное
принимаем
3.2.4. Определяем число зубьев шестерни по формуле:
(3.21)
где: — диаметр шестерни, мм;
-
угол наклона зубьев, град.;
- модуль, мм.
Минимальное число зубьев равно:
(3.22)
Так
как расчетное количество зубьев шестерни
меньше минимального принимаем
.
3.2.5. Определяем число зубьев колеса по формуле:
(3.23)
где:
- число зубьев шестерни;
- передаточное число передачи.
3.3. Расчет геометрических и кинематических параметров передачи.
3.3.1. Определяем делительное межосевое расстояние по формуле:
(3.24)
где: - число зубьев шестерни;
-
число зубьев колеса;
- угол наклона зубьев, град.;
- модуль, мм.
Начальное
межосевое расстояние выбираем равным
135 мм, т.е.
3.3.2. Определяем угол наклона зубьев по формуле:
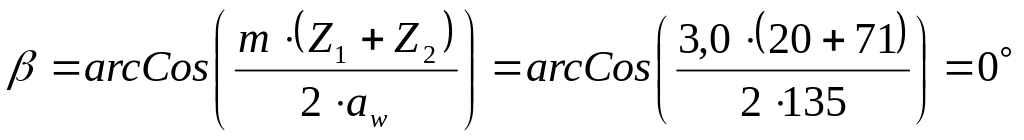(3.25)
где: - число зубьев шестерни;
- число зубьев колеса;
-
начальное межосевое расстояние, мм;
- модуль, мм.
3.3.3. Определяем основной угол наклона зуба по формуле:
(3.26)
где: - угол наклона зубьев, град.;
3.3.4. Определяем делительный угол профиля в торцевом сечении:
(3.27)
где: - угол наклона зубьев, град.;
3.3.5. Определяем угол зацепления при выполнении передачи со смещением:
(3.28)
3.3.6. Коэффициент суммы смещений:
(3.29)
где:
- смешение исходного контура шестерни,
мм;
-
смешение исходного контура колеса, мм.
3.3.7. Определяем начальный диаметр шестерни по формуле:
(3.30)
где: - начальное межосевое расстояние, мм;
- передаточное число передачи.
3.3.8. Определяем начальный диаметр колеса по формуле:
(3.31)
где: - начальное межосевое расстояние, мм;
- передаточное число передачи.
Уточненное значение ширины зубчатого венца:
3.3.9. Коэффициенты воспринимаемого и уравнительного смещений:
(3.32)
3.3.10. Определяем делительный диаметр шестерни по формуле:
(3.33)
где: - число зубьев шестерни;
- модуль, мм.
3.3.11 Определяем делительный диаметр колеса по формуле:
(3.34)
где: - число зубьев колеса;
- модуль, мм.
3.3.12. Определяем диаметр вершин зубьев шестерни по формуле:
(3.35)
где: - коэффициент смещения исходного контура шестерни;
- модуль, мм;
-
коэффициент уравнительного смещения;
-
делительный диаметр шестерни, мм.
3.3.13 Определяем диаметр вершин зубьев колеса по формуле:
(3.36)
где: - коэффициент смещения исходного контура шестерни;
- модуль, мм;
- коэффициент уравнительного смещения;
-
делительный диаметр колеса, мм.
3.3.14. Определяем диаметр впадин шестерни по формуле:
(3.37)
где: - коэффициент смещения исходного контура шестерни;
- модуль, мм;
- делительный диаметр шестерни, мм.
3.3.15. Определяем диаметр впадин колеса по формуле:
(3.38)
где: - коэффициент смещения исходного контура шестерни;
- модуль, мм;
- делительный диаметр колеса, мм.
3.3.16. Определяем основной диаметр шестерни по формуле:
(3.39)
где:
- делительный угол профиля в торцевом
сечении;
- делительный диаметр шестерни, мм.
3.3.17. Определяем основной диаметр колеса по формуле:
(3.40)
где: - делительный угол профиля в торцевом сечении;
- делительный диаметр колеса, мм.
3.3.18. Определяем коэффициент торцевого перекрытия по формуле:
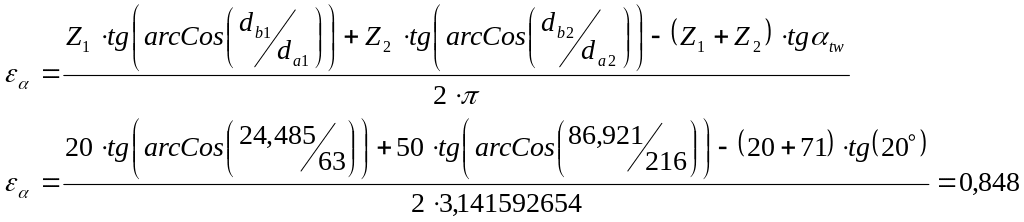(3.41)
где:
- угол зацепления при выполнении передачи
со смещением;
-
диаметр вершин шестерни, мм;
-
диаметр вершин колеса, мм;
-
основной диаметр шестерни, мм;
-
основной диаметр колеса, мм;
- число зубьев шестерни;
- число зубьев колеса.
3.3.19. Определяем коэффициент осевого перекрытия по формуле:
(3.42)
где: - угол наклона зубьев, град.;
- модуль, мм;
- ширина зубчатого венца колеса, мм.
3.3.20. Определяем суммарный коэффициент перекрытия по формуле:
(3.43)
где:
- коэффициент торцевого перекрытия;
-
коэффициент осевого перекрытия.
3.3.21. Определяем окружную скорость по формуле:
(3.44)
где: - делительный диаметр шестерни, мм;
-
частота вращения шестерни, об/мин.
3.3.22. Определяем эквивалентное число зубьев шестерни по формуле:
(3.45)
где: - число зубьев шестерни;
- угол наклона зубьев, град.
3.3.23. Определяем эквивалентное число зубьев колеса по формуле:
(3.46)
где: - число зубьев колеса;
- угол наклона зубьев, град.
3.4. Проверочные расчеты передачи.
3.4.1. Проверочный расчет на контактную выносливость:
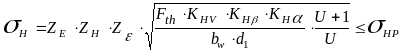(3.47)
где:
- коэффициент, учитывающий механические
свойства материалов сопряженных зубчатых
колес.
Для
стальных передач при
,
;
-
коэффициент, учитывающий форму сопряженных
поверхностей зубьев в полюсе зацепления:
(3.48)
где: - угол зацепления при выполнении передачи со смещением;
-
делительный угол профиля в торцевом
сечении;
-
основной угол наклона зуба.
-
коэффициент, учитывающий суммарную
длину контактных линий:
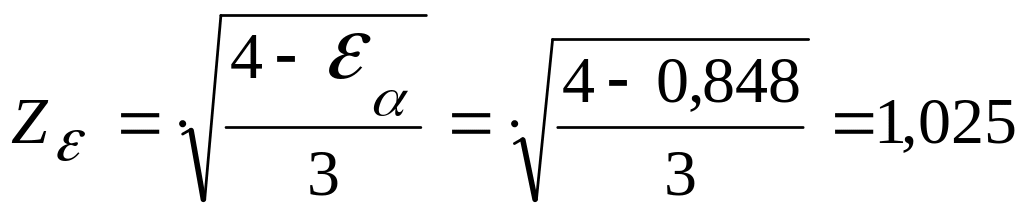(3.49)
где: - коэффициент торцевого перекрытия.
-
окружная сила на делительном цилиндре,
Н:
(3.50)
где:
- исходная расчетная нагрузка, в качестве
которой принимается наибольший из
действующих на шестерню вращающий
момент в Нм, для которого число циклов
перемен напряжений не менее
.
В данном случае
;
-
делительный диаметр шестерни, мм.
- коэффициент,
учитывающий влияние вида зубчатой
передачи(выбирается по таблице):
Твердость поверхностей зубьев по Виккерсу |
Вид зубьев |
Значение коэффициента |
или
|
Прямые
Косые |
0,06
0,02 |
и
|
Прямые
Косые |
0,14
0,04 |
Таблица 3.2.
Так
как передача прямозубая и твердость
колеса менее 350 единиц по Виккерсу, то
принимаем
.
-
коэффициент, учитывающий влияние
разности шагов зацепления зубьев
шестерни и колеса:
Значение
коэффициента
Модуль ,мм |
Степень точности по нормам плавности по ГОСТ 1643–81 |
|||||
|
5 |
6 |
7 |
8 |
9 |
10 |
до 3,5 |
2,8 |
3,8 |
4,7 |
5,6 |
7,3 |
10,0 |
св. 3,5 до 10 |
3,1 |
4,2 |
5,3 |
6,1 |
8,2 |
11,0 |
св. 10 |
3,7 |
4,8 |
6,4 |
7,3 |
10,0 |
13,5 |
Таблица 3.3.
Так
как модуль менее 3,5 мм и выбранная степень
точности - 8 , то
-
удельная окружная динамическая сила,
Н/мм:
(3.51)
где: - коэффициент, учитывающий влияние вида зубчатой передачи;
- коэффициент, учитывающий влияние разности шагов зацепления зубьев шестерни и колеса;
-
окружная скорость, м/с;
-
начальное межосевое расстояние, принятое
для изготовления передачи, мм;
- передаточное отношение передачи.
Значение
коэффициента
Модуль ,мм |
Степень точности по нормам плавности по ГОСТ 1643–81 |
|||||
|
5 |
6 |
7 |
8 |
9 |
10 |
до 3,5 |
85 |
160 |
240 |
380 |
700 |
1200 |
св. 3,5 до 10 |
105 |
194 |
310 |
410 |
880 |
1500 |
св. 10 |
150 |
250 |
450 |
590 |
1050 |
1800 |
Таблица 3.4.
Так
как модуль менее 3,5 мм и выбранная степень
точности - 8 , то
-
коэффициент, учитывающий динамическую
нагрузку, возникающую в зацеплении до
зоны резонанса:
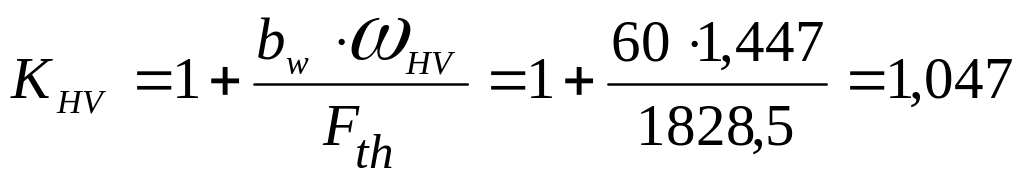(3.52)
где: - удельная окружная динамическая сила, Н/мм;
- окружная сила на делительном цилиндре, Н;
-
ширина зубчатого венца колеса, мм.
-
коэффициент, учитывающий неравномерность
распределения нагрузки по длине
контактных линий в начальный период
работы передачи:
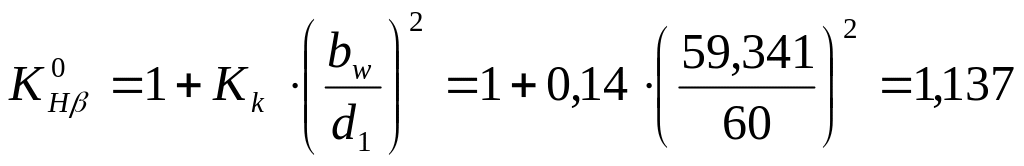(3.53)
где: - делительный диаметр шестерни, мм;
при
расположении шестерни на валу передачи
со стороны подвода вращающего момента;
- ширина зубчатого венца колеса, мм.
-
коэффициент, учитывающий приработку
зубьев:
(3.54)
где:
- среднее значение твердости рабочей
поверхности зуба шестерни;
- окружная скорость, м/с;
-
коэффициент, учитывающий неравномерность
распределения нагрузки по длине
контактных линий
(3.55)
где: - коэффициент, учитывающий приработку зубьев;
- коэффициент, учитывающий неравномерность распределения нагрузки по длине контактных линий в начальный период работы передачи.
-
коэффициент, учитывающий распределение
нагрузки между зубьями. Так как передача
прямозубая, то принимаем
.
Подставляем полученные значения коэффициентов в формулу (3.47) и вычисляем напряжения:
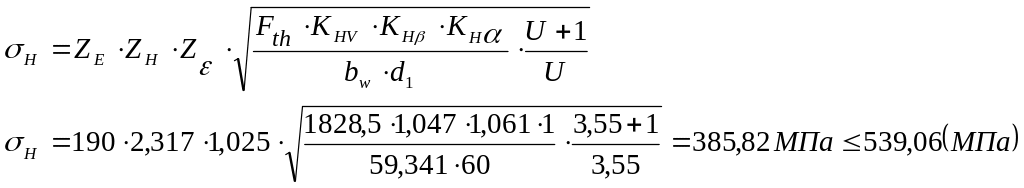
Напряжения, полученные при расчете от действия реальной нагрузки, возникающей в процессе работы, меньше допустимых.