4 Оптимизация
В данной лабораторной работе мы ограничимся рассмотрением только некоторых возможных направлений оптимизации.
1.
Предположим, расчеты показали, что,
реализуя первоначальный сетевой график,
мы не уложимся в заданный срок - Ткр
>
(см.
лекцию). В
этом случае для завершения всего
комплекса работ в заданный срок
длительность критического пути можно
изменить за счет привлечения дополнительных
ресурсов.
Проанализируем, например, возможность уменьшения длительности отдельных работ. Длительность выполнения работы 5-7 можно уменьшить, если, например, увеличить число станков. Если принимается двукратное увеличение числа станков, то значение длительности работы 5-7 вместо 8 будет 4 единицы, что, в принципе, может привести к изменению критического пути сети и соответствующему изменению ее характеристик.
Процесс пересчета сетевого графика в этом случае становится итерационным и за определенное количество шагов Ткр приблизится к (вспомните симплекс-метод).
2. Для того, чтобы высвободить ресурсы для их использования на других работах можно воспользоваться полным резервом времени работы. Например, полный резерв (1,3) времени работы а13, равный (1,3) = 5, может быть использован
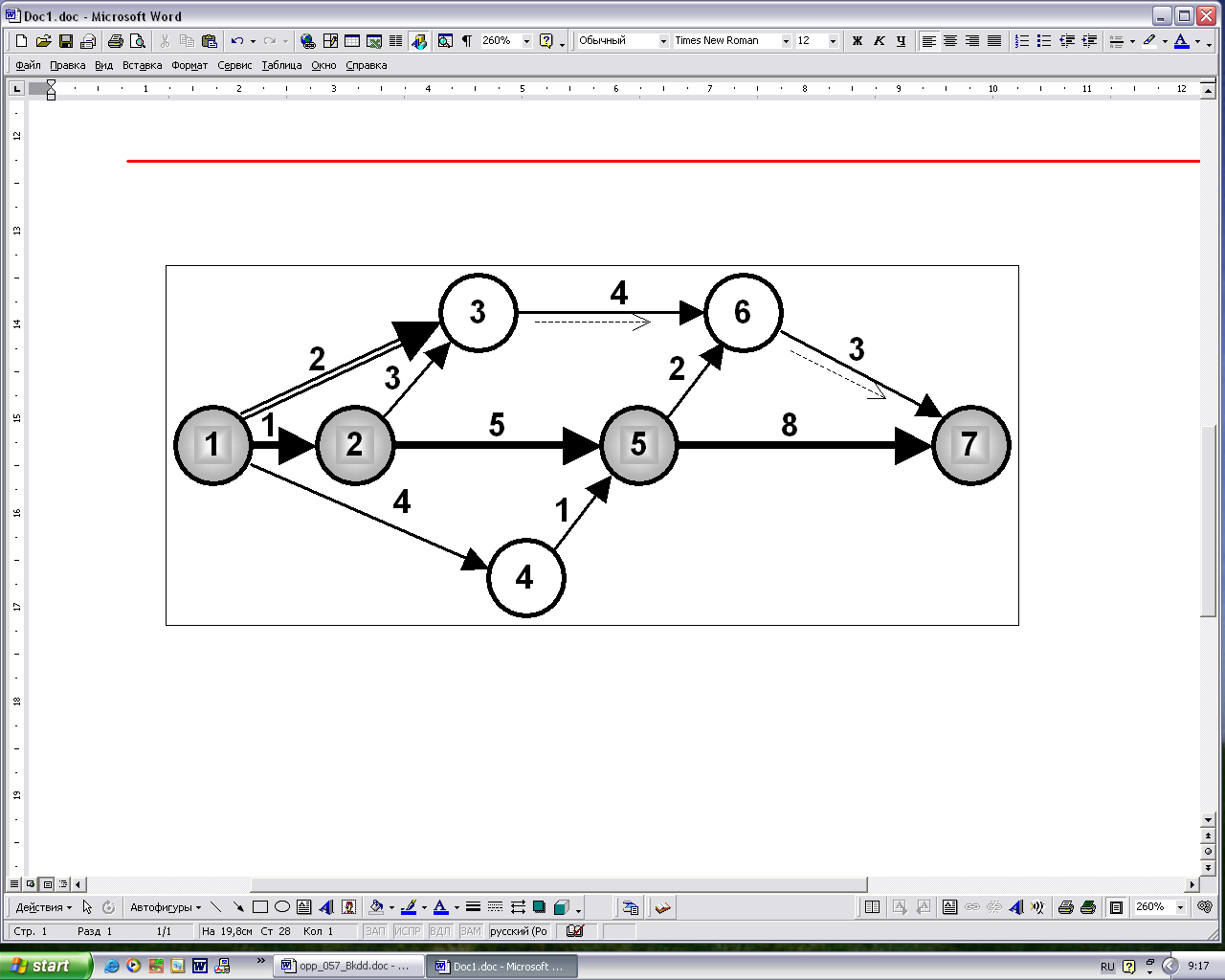
Рис. 2. Полный резерв (1,3) времени работы а1-3 равен 5.
для увеличения длительности либо работы а1-3, либо работ а3-6 и
а6-7, лежащих на пути, проходящем через эту работу. Он может быть распределен каким-либо образом между этими работами.
Далее, в результате анализа мы приходим к выводу, что полный резерв (1,4) времени работы а1-4, равный (1,4) = 1, может быть использован
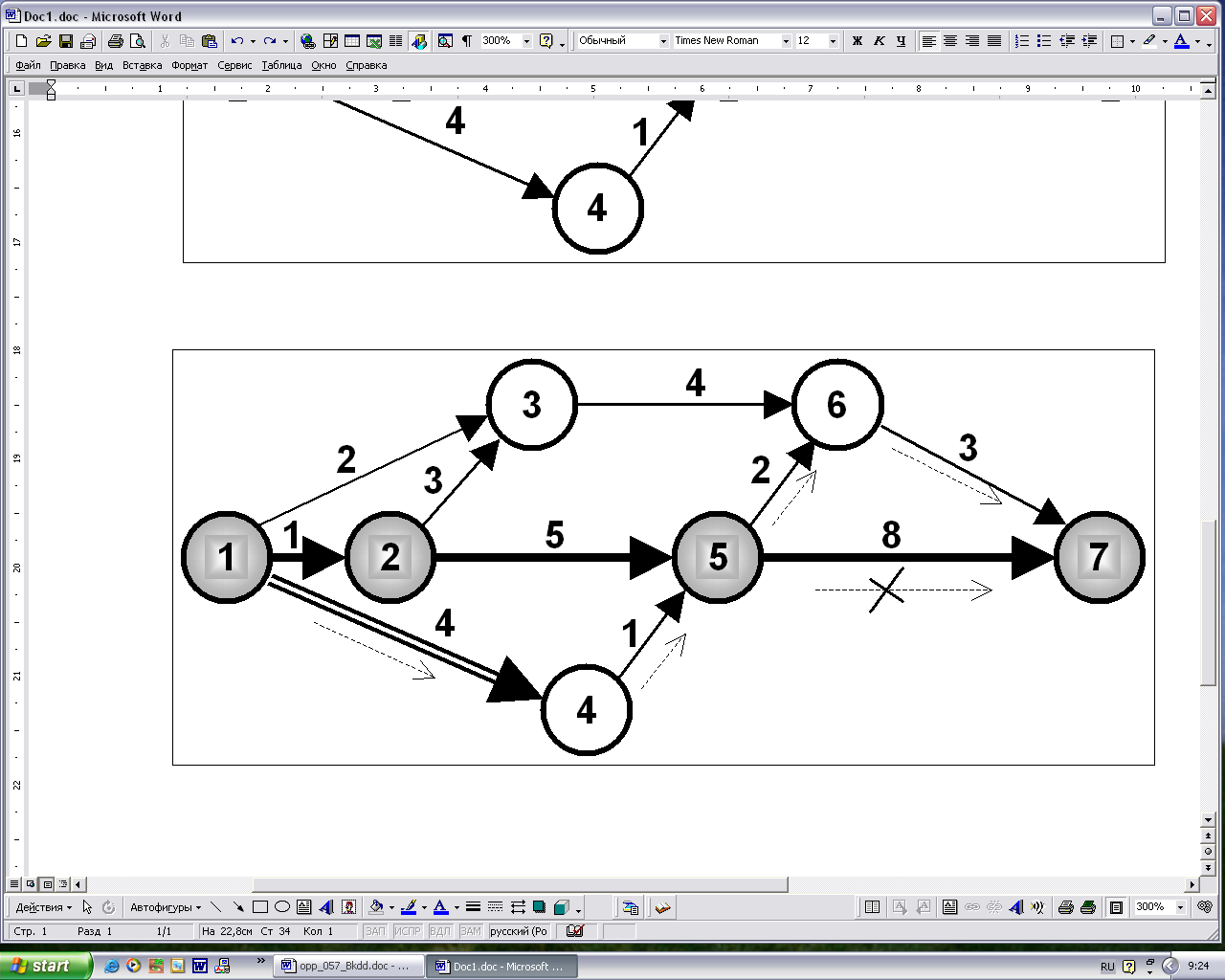
Рис. 3. Полный резерв (1,4) времени работы а1-4 равен 1.
для увеличения длительности работ (см. рис. 3) а1-4, а4-5, а5-6, а6-7, но не для увеличения продолжительности работы а57, так как она лежит на критическом пути. Процесс анализа полных резервов времени работы нужно продолжить (а2-3, а3-6, а4-5, а5-6, а6-7). Для большей гарантии такие расчеты необходимо провести применительно к полным резервам.
5. Замечание
Как отмечалось на лекции, возможно принципиально другое визуальное представление сетевых графиков – в форме двойственного графа
а1-3
а3-6
а6-7
а2-3
а5-6
а1-2
а2-5
а1-4
а4-5
а5-7
Рис. 4. Граф двойственный графу рис. 3.
На рис. 4 приведен пример такого представления: работы – в узлах, события – на дугах.
Индивидуальные задания
Каждый студент получает индивидуальное задание на исследование. Номер варианта задания совпадает с номером фамилии студента в групповом журнале.
Каждый вариант задания содержит описание работ в виде таблицы.
|
Вариант 30 |
||
1 |
2-10 |
3-12 |
4-20 |
2 |
7-34 |
|
|
3 |
5-17 |
6-18 |
8-40 |
4 |
6-10 |
|
|
5 |
7-19 |
|
|
6 |
8-20 |
|
|
7 |
8-7 |
|
|
Первый столбец таблицы содержит номера вершин (событий) задаваемой сети.
В последующих столбцах табл. 2 указываются (через дефис) номера вершин, с которыми соединена рассматриваемая вершина, и значение длительности работы. Так, например, вершина 1 (исток, исходная вершина) соединяется с тремя вершинами: с вершиной 2 (значение длительности работы при этом равно 10), с вершиной 3 (работа - 12) и с вершиной 4 (работа - 20). Вершина 2 соединяется лишь с вершиной 7 через работу – 34….
Как видно из таблицы сеть состоит из восьми вершин, причем восьмая вершина является стоком, конечной вершиной сети.
По заданию студент должен:
1.
построить сеть в виде графа, на котором указать номера всех вершин и характеристики дуг;
определить количество (m) и продолжительности (t(i), i = 1, 2, 3, …, m) всех полных путей;
определить критический путь и его характеристики;
определить резервы времени полных путей Ri, i = 1, 2, 3, …, m; m – количество полных путей;
определить основные параметры сетевого графика:
ранний срок начала работы tрн;
ранний срок окончания работ tро;
поздний срок окончания работ tпо;
поздний срок начала работ tпн;
полные резервы времени каждой работы (i,j).
Найденные значения заносятся в результирующую таблицу и используются для принятия решения по оптимизации сети.
2. Выбрать варианты оптимизации. Варианты оптимизированных сетей с краткими характеристиками представить в виде отчета.
3. Рекомендуется построить двойственный граф: работы в узлах, а события – дуги. На двойственном графе проанализировать варианты перераспределения резервов и возможности смещения ранних и поздних сроков начала и окончания работ
В отчете должны быть следующие подпункты.
Ведение.
Исходные данные
Вариант изображения исходного графика, согласно исходным данным
Определение количества и продолжительности всех путей
Определение резервов времени полных путей
Определение основных параметров сетевого графика (см. таблицу 1)
Оптимизация сетевого графика
Двойственный граф.
Заключение
Таблица 3. Табличные задания вариантов.
|
Вариант 01 |
|
Вариант 02 |
|
Вариант 03 |
|
Вариант 04 |
|
Вариант 05 |
||||||||||
1 |
2-10 |
3-12 |
4-20 |
1 |
2-12 |
3-14 |
|
1 |
2-1 |
3-2 |
4-2 |
1 |
2-5 |
3-6 |
4-10 |
1 |
2-21 |
4-12 |
|
2 |
7-34 |
|
|
2 |
4-18 |
7-24 |
|
2 |
7-4 |
|
|
2 |
7-17 |
|
|
2 |
3-20 |
7-17 |
|
3 |
5-17 |
6-18 |
8-40 |
3 |
5-17 |
6-18 |
8-20 |
3 |
5-7 |
6-8 |
|
3 |
5-8 |
6-9 |
|
3 |
5-15 |
6-11 |
8-19 |
4 |
6-10 |
|
|
4 |
6-15 |
|
|
4 |
6-1 |
|
|
4 |
6-5 |
|
|
4 |
6-11 |
|
|
5 |
7-19 |
|
|
5 |
8-10 |
|
|
5 |
7-9 |
|
|
5 |
7-10 |
8-10 |
|
5 |
7-13 |
|
|
6 |
8-20 |
|
|
6 |
8-17 |
|
|
6 |
8-2 |
|
|
6 |
8-10 |
|
|
6 |
8-11 |
|
|
7 |
8-7 |
|
|
7 |
8-19 |
|
|
7 |
8-7 |
|
|
7 |
8-8 |
|
|
7 |
8-17 |
|
|
8 |
9-17 |
|
|
8 |
9-10 |
|
|
8 |
9-13 |
|
|
8 |
9-8 |
|
|
8 |
9-12 |
|
|
|
Вариант 06 |
|
Вариант 07 |
|
Вариант 08 |
|
Вариант 09 |
|
Вариант 10 |
||||||||||
1 |
2-11 |
3-13 |
4-23 |
1 |
2-10 |
3-12 |
4-20 |
1 |
2-10 |
3-12 |
4-20 |
1 |
2-15 |
3-24 |
4-29 |
1 |
2-8 |
4-9 |
|
2 |
7-32 |
|
|
2 |
7-34 |
|
|
2 |
7-34 |
|
|
2 |
5-12 |
|
|
2 |
3-5 |
7-34 |
|
3 |
4-22 |
5-18 |
8-38 |
3 |
5-17 |
6-18 |
|
3 |
5-17 |
6-18 |
8-20 |
3 |
5-17 |
6-18 |
8-40 |
3 |
5-17 |
6-18 |
8-10 |
4 |
6-15 |
|
|
4 |
6-10 |
|
|
4 |
6-10 |
|
|
4 |
3-10 |
|
|
4 |
6-10 |
|
|
5 |
7-17 |
|
|
5 |
7-19 |
8-14 |
|
5 |
7-19 |
|
|
5 |
7-19 |
8-40 |
|
5 |
7-11 |
|
|
6 |
8-23 |
|
|
6 |
8-20 |
|
|
6 |
8-20 |
|
|
6 |
8-20 |
|
|
6 |
8-8 |
|
|
7 |
8-17 |
|
|
7 |
8-7 |
|
|
7 |
8-8 |
|
|
7 |
8-7 |
|
|
7 |
8-17 |
|
|
8 |
9-13 |
|
|
8 |
9-7 |
|
|
8 |
9-7 |
|
|
8 |
9-11 |
|
|
8 |
9-17 |
|
|
|
Вариант 11 |
|
Вариант 12 |
|
Вариант 13 |
|
Вариант 14 |
|
Вариант 15 |
||||||||||
1 |
2-1 |
3-1 |
4-2 |
1 |
2-5 |
3-7 |
4-9 |
1 |
2-3 |
3-4 |
4-7 |
1 |
2-10 |
3-12 |
4-11 |
1 |
2-2 |
3-3 |
4-4 |
2 |
5-3 |
|
|
2 |
7-7 |
|
|
2 |
7-12 |
|
|
2 |
3-5 |
7-13 |
|
2 |
7-11 |
|
|
3 |
5-7 |
6-8 |
8-4 |
3 |
5-9 |
6-4 |
8-12 |
3 |
5-6 |
6-6 |
8-13 |
3 |
5-17 |
6-18 |
8-11 |
3 |
5-4 |
6-5 |
8-9 |
4 |
6-1 |
|
|
4 |
6-4 |
8-2 |
|
4 |
6-3 |
|
|
4 |
6-11 |
|
|
4 |
6-2 |
|
|
5 |
7-9 |
8-4 |
|
5 |
7-5 |
|
|
5 |
7-6 |
8-8 |
|
5 |
7-10 |
|
|
5 |
7-3 |
|
|
6 |
8-2 |
|
|
6 |
8-3 |
|
|
6 |
8-7 |
|
|
6 |
8-12 |
|
|
6 |
8-5 |
|
|
7 |
8-9 |
|
|
7 |
8-5 |
|
|
7 |
8-4 |
|
|
7 |
8-6 |
|
|
7 |
8-9 |
|
|
8 |
9-7 |
|
|
8 |
9-15 |
|
|
8 |
9-2 |
|
|
8 |
9-5 |
|
|
8 |
9-7 |
|
|
|
Вариант 16 |
|
Вариант 17 |
|
Вариант 18 |
|
Вариант 19 |
|
Вариант 20 |
||||||||||
1 |
2-1 |
3-2 |
4-2 |
1 |
2-1 |
3-1 |
4-1 |
1 |
2-3 |
3-3 |
4-3 |
1 |
2-1 |
3-2 |
4-3 |
1 |
2-11 |
3-11 |
4-11 |
2 |
7-3 |
|
|
2 |
7-1 |
|
|
2 |
7-3 |
|
|
2 |
7-4 |
|
|
2 |
7-11 |
|
|
3 |
5-7 |
6-8 |
8-4 |
3 |
5-1 |
6-2 |
|
3 |
5-3 |
6-3 |
8-3 |
3 |
5-5 |
6-6 |
|
3 |
5-11 |
6-11 |
8-11 |
4 |
6-1 |
|
|
4 |
6-2 |
|
|
4 |
6-3 |
|
|
4 |
6-7 |
|
|
4 |
6-5 |
|
|
5 |
7-9 |
|
|
5 |
7-2 |
|
|
5 |
7-3 |
|
|
5 |
7-8 |
|
|
5 |
7-5 |
|
|
6 |
8-2 |
|
|
6 |
8-2 |
|
|
6 |
8-3 |
|
|
6 |
8-9 |
|
|
6 |
8-5 |
|
|
7 |
8-17 |
|
|
7 |
8-5 |
|
|
7 |
8-11 |
|
|
7 |
8-9 |
|
|
7 |
8-5 |
|
|
8 |
9-17 |
|
|
8 |
9-7 |
|
|
8 |
9-3 |
|
|
8 |
9-9 |
|
|
8 |
9-7 |
|
|
|
Вариант 21 |
|
Вариант 22 |
|
Вариант 23 |
|
Вариант 24 |
|
Вариант 25 |
||||||||||
1 |
2-2 |
3-3 |
4-4 |
1 |
2-10 |
3-12 |
4-7 |
1 |
2-10 |
3-12 |
4-20 |
1 |
2-1 |
3-1 |
4-2 |
1 |
2-20 |
3-12 |
4-10 |
2 |
7-7 |
|
|
2 |
7-8 |
|
|
2 |
7-34 |
|
|
2 |
7-3 |
|
|
2 |
7-15 |
|
|
3 |
5-3 |
6-4 |
|
3 |
5-17 |
6-18 |
8-5 |
3 |
5-17 |
6-18 |
|
3 |
5-1 |
6-1 |
8-4 |
3 |
5-15 |
6-9 |
8-9 |
4 |
6-2 |
|
|
4 |
6-10 |
|
|
4 |
6-10 |
|
|
4 |
6-1 |
|
|
4 |
6-11 |
|
|
5 |
7-4 |
|
|
5 |
7-7 |
|
|
5 |
7-19 |
|
|
5 |
7-1 |
|
|
5 |
7-5 |
|
|
6 |
8-4 |
|
|
6 |
8-6 |
|
|
6 |
8-20 |
|
|
6 |
8-2 |
|
|
6 |
8-8 |
|
|
7 |
8-4 |
|
|
7 |
8-9 |
|
|
7 |
8-17 |
|
|
7 |
8-7 |
|
|
7 |
8-11 |
|
|
8 |
9-12 |
|
|
8 |
9-7 |
|
|
8 |
9-13 |
|
|
8 |
9-3 |
|
|
8 |
9-9 |
|
|
|
Вариант 26 |
|
Вариант 27 |
|
Вариант 28 |
|
Вариант 29 |
|
Вариант 30 |
||||||||||
1 |
2-5 |
3-6 |
4-10 |
1 |
2-10 |
3-12 |
4-20 |
1 |
2-13 |
3-9 |
4-7 |
1 |
2-1 |
3-2 |
4-2 |
1 |
2-10 |
3-12 |
4-20 |
2 |
7-17 |
|
|
2 |
7-34 |
|
|
2 |
7-11 |
|
|
2 |
7-4 |
|
|
2 |
7-34 |
|
|
3 |
5-8 |
6-9 |
8-10 |
3 |
5-17 |
6-18 |
8-40 |
3 |
5-9 |
8-10 |
|
3 |
5-7 |
6-8 |
|
3 |
5-17 |
6-18 |
8-40 |
4 |
6-5 |
|
|
4 |
6-10 |
|
|
4 |
6-20 |
|
|
4 |
6-1 |
|
|
4 |
6-10 |
|
|
5 |
7-10 |
|
|
5 |
7-19 |
|
|
5 |
7-20 |
|
|
5 |
7-9 |
|
|
5 |
7-19 |
|
|
6 |
8-10 |
|
|
6 |
8-20 |
|
|
6 |
8-20 |
|
|
6 |
8-2 |
|
|
6 |
8-20 |
|
|
7 |
8-10 |
|
|
7 |
8-14 |
|
|
7 |
8-15 |
|
|
7 |
8-12 |
|
|
7 |
8-13 |
|
|
8 |
9-10 |
|
|
8 |
9-7 |
|
|
8 |
9-5 |
|
|
8 |
9-9 |
|
|
8 |
9-7 |
|
|