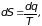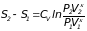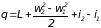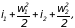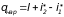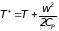3.4. Понятие об энтропии

В термодинамике есть еще одна очень важная функция состояния газа  энтропия (S). Математически прирост энтропии dS определяется выражением

(3.19)

где dq  полное количество тепла, подводимое к газу как извне, так и изнутри за счет сил трения;

Т  абсолютная температура.

Если в формуле (2.9) вместо dq подставить его выражение согласно первому закону термодинамики

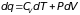
и произвести ряд преобразований, то можно получить

(3.20)

Согласно (2.10) в идеальном адиабатическом процессе, который является обратимым, изменение энтропии равно нулю, так как в этом случае

и изменение энтропии не происходит. В реальном адиабатическом процессе за счет трения выделяется тепло (dq_тр>0) и процесс протекает в таком направлении, что энтропия возрастает S₂-S₁0.

Таким образом, численное значение S₂-S₁, может служить мерой потерь механической энергии на преодоление сил трения. Если известны параметры состояния газа в точках 1 и 2, то изменение энтропии в процессе 1  2 определяется по формуле (3.20).

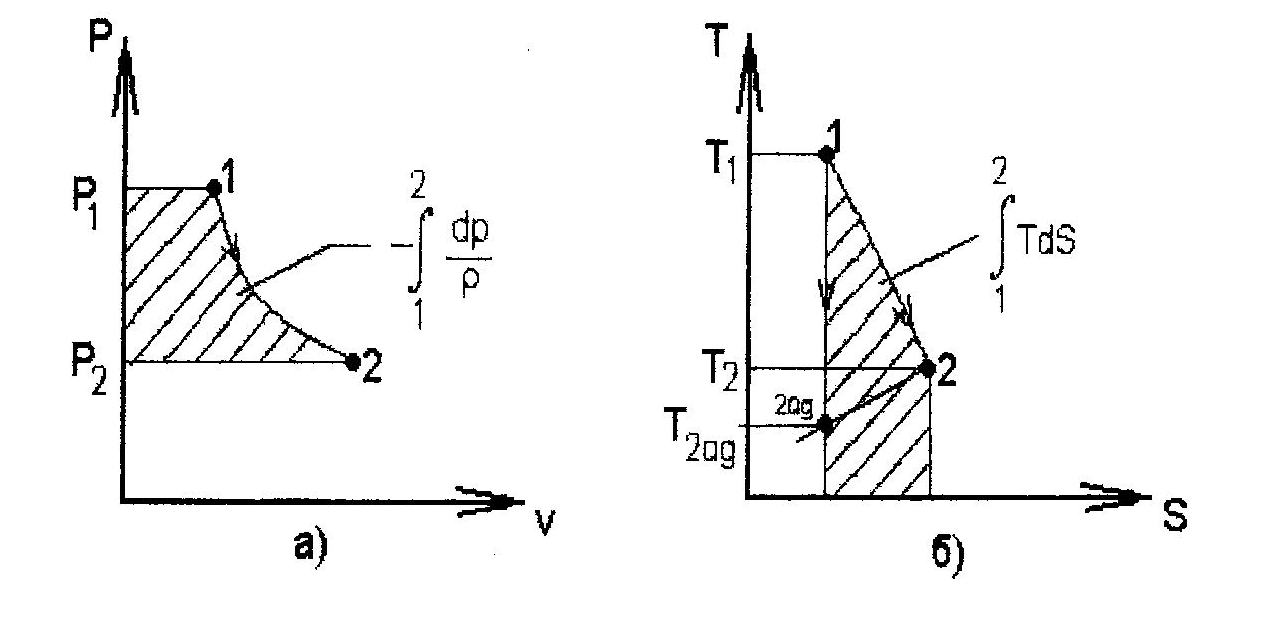
Рис. 3.4. Процесс расширения газов

В термодинамике процессы принято представлять в Р  V и Т  S координатах (рис. 3.4).

На рис. 3.4, а представлен процесс расширения газа в турбине. Заштрихованная площадь характеризует техническую работу, которая может быть получена на валу турбины. На рис. 3.4, б тот же процесс представлен в координатах Т  S. Здесь заштрихованная площадь характеризует количество тепла, выделившееся в результате работы, затраченной на преодоление сил трения. Если бы процесс был идеальным, т.е. шел без потерь энергии на трение, то он изображался бы вертикальным отрезком 1  2ад. Соответственно площадь под отрезком 1  2ад равна нулю. Таким образом, использование энтропии позволяет количественно оценить потери механической энергии на трение.

3.5. Частные случаи уравнения энергии

Запишем еще раз уравнение энергии

(3.21)

При отсутствии технической работы (отсутствует турбина или компрессор в потоке газа) и теплообмена с окружающей средой имеем

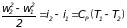
Из этого уравнения следует, что изменение скорости в энергетически изолированном потоке газа (q=0, L = 0) однозначно связано с изменением температуры. Если скорость газа не изменяется, то остается постоянной и температура независимо от того, есть трение или нет. Процесс расширения газа в канале от давления Р₁ до давления Р₂ можно представить на диаграмме в Т  S координатах (рис. 3.5).

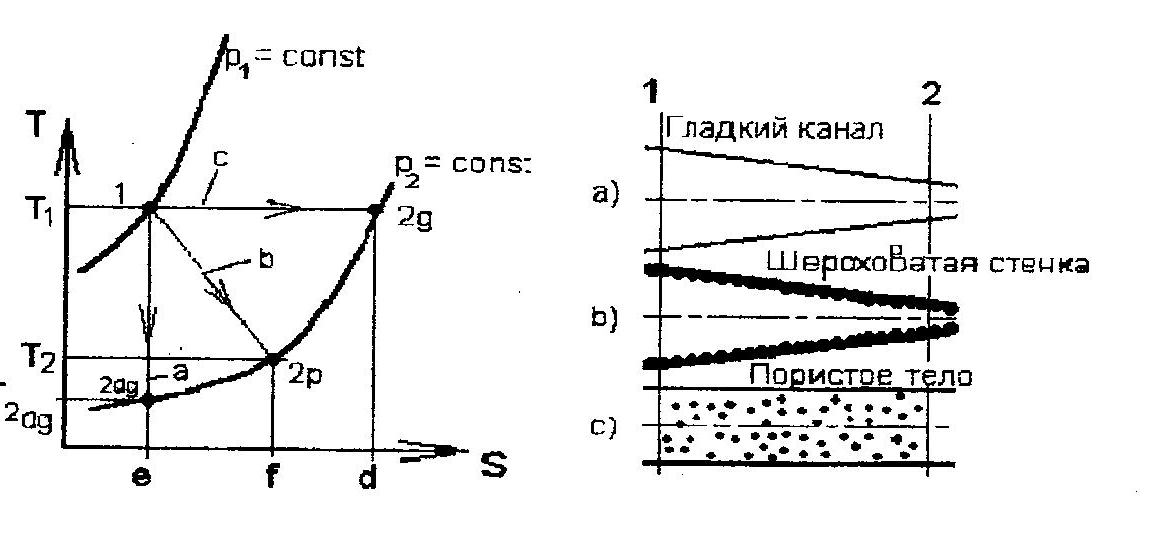
Рис. 3.5. Процесс расширения газа: а  идеальная адиабата; в  расширение газа с трением; с  адиабатическое дросселирование

Расширение газа от давления Р₁ до давления Р₂ может идти различными способами. Процесс расширения а соответствует идеальной адиабате. Потерь на трение нет. Увеличение скорости на участке канала 1  2 максимальное; уменьшение температуры также максимальное. Уравнение энергии для случая а

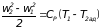
Другой случай  с. Вся потенциальная энергия газа переходит в тепло. Скорость не увеличивается, температура не изменяется. Количество тепла, выделившееся в результате работы сил трения, соответствует площади треугольника 1 2 g d е. Уравнение энергии для случая с

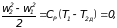
откуда w₂=w₁ и T₁=T_2д.

Случай в соответствует течению газа по сужающемуся каналу с трением. Скорость увеличивается. Тепло, выделившееся в результате работы сил трения, соответствует площади 1 2 р f е. Уравнение энергии для случая в

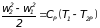
Уравнение энергии (3.21) можно записать в виде

(3.22)

т.е. суммы энтальпии и кинетической энергии газа для энергетически изолированного потока газа в сечениях 1 и 2 равны между собой. Это соотношение можно записать и для любых других сечений. Поэтому уравнение (3.22) записывается без индексов в виде

Отсюда видно, что если поток газа затормозить полностью (w=0), то энтальпия достигнет максимально возможного значения

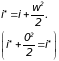
Получающееся при этом значение энтальпии i* будем называть полной энтальпией, а соответствующую ей абсолютную температуру

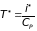
температурой торможения.

В дальнейшем всем параметрам, определенным для заторможенного потока газа будет, присваиваться верхний индекс *.

С помощью (3.23) из уравнения энергии можно исключить скорости, и тогда уравнение энергии записывается в виде

(3.24)

Теплоемкость С_р не является строго постоянной величиной, а изменяется в зависимости от температуры, но незначительно. Пользуясь средним значением теплоемкости, можно вычислить температуру торможения по следующей формуле

(3.25)

Для воздуха С_р=1005 Дж/кг К и, следовательно,

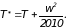
В воздушном потоке с нормальной температурой воздуха 300 К при скорости движения w=100; 350; 1000 м/с получается соответственно температура торможения Т^*=305, 360,800 К.

Итак, температура торможения за входным устройством самолета (перед компрессором) может быть определена по формуле (3.25).

Для расчета компрессора или турбины обычно пользуются уравнением энергии в форме (3.24). Так как принято, что работа турбины положительна I_K>0, а работа компрессора 1_К<0, то для турбины имеем

(3.26)

а для компрессора

(3.27)

Здесь принято, что сечение 1 на входе в компрессор, турбину, а сечение 2 на выходе из компрессора, турбины. По (3.26) можно определить температуру на выходе из турбины T₂^*, если известны температура на входе Т₁^* и работа на валу турбины I_T По (3.27) можно определить температуру на выходе из компрессора Т₂^*, если известны температура на входе Т₁^* и работа, подводимая к валу компрессора I_K.

В формулах (3.26) и (3.27) потери на трение в подшипниках, трение дисков о газ или воздух, перетекание через радиальный зазор в лопаточных машинах не учитываются. Применительно к камере сгорания I = 0 уравнение энергии (3.24) будут иметь вид

(3.28)

где g_T  количество топлива, приходящееся на 1 кг воздуха;

Н_u  теплотворная способность топлива т.е. количество тепла, выделяющееся при сгорании 1 кг топлива, кДж/кг;

С_P2  теплоемкость продуктов сгорания, кДж/кг К;

С_P1  теплоемкость воздуха, кДж/кг К;

Т₂*  температура продуктов сгорания, К;

Т₁^*  температура воздуха на входе в камеру сгорания, К.

Уравнение (3.28) записано для 1 кг воздуха. Расход продуктов сгорания больше расхода воздуха на величину g_Т, поэтому в правой части уравнения (3.28) появился сомножитель (1+g_T). Уравнение (3.28) дает возможность определить расход топлива для получения необходимой температуры Т₂^*.