1.9.8. Формула Тейлора.

Пусть функция f(x₁, ..., x_m) задана и n+1 раз дифференцируема в некоторой окрестности точки М₀( ), тогда для всех точек М(х₁,...,х_m) из этой окрестности справедлива формула

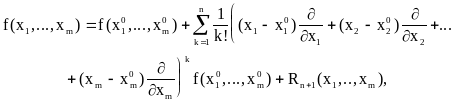
где

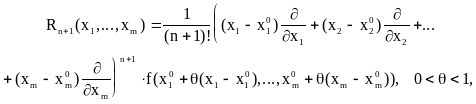
где  зависит, вообще говоря, от М(х₁,...,х_m).

Заметим, что в принятых нами символических обозначениях

причем .

Таким образом, формула Тейлора может быть записана более компактно:

где

, 0<θ<1

Замечание 1. При более слабых предположениях, а именно, если f(x₁,...,x_m) дифференцируема (n-1) раз в окрестности т.М₀ и n раз в самой точке М₀, для остаточного члена в формуле Тейлора R_n+1(x₁,...,x_m) справедливо представление R_n+1(x₁,...,x_m) = 0(ⁿ) (форма Пеано), где

.

Замечание 2. В случае двух переменных (u=f(x,y)) формула Тейлора второго порядка в развернутом виде записывается следующим образом:

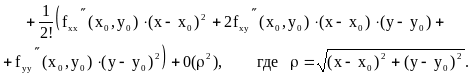
Пример 1. Разложить по формуле Тейлора второго порядка в окрестности т. (1,1) функцию f(x,y) = x³ - 3xy³ + xy - y² + 6x - y + 1

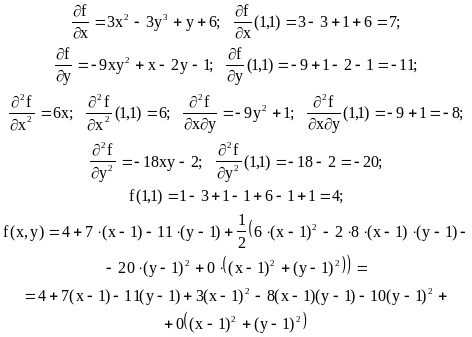
Пример 2. Разложить по формуле Маклорена до членов третьего порядка функцию (по формуле Тейлора с центром в т.М₀(0,0)). Последовательно находим дифференциалы функции u до третьего порядка включительно.

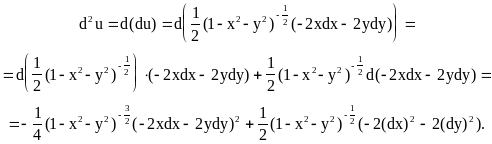
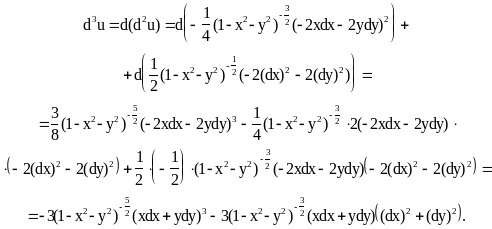
Полагая здесь x=y=0, dx=x, dy=y, получаем

u(0,0)=1; du(0,0)=0; d²u(0,0)= -(x²+y²); d³u=0

и

u(x,y) .

1.9.9. Неявные функции.

Пусть задано уравнение f(x,y)=0, где f - дифференцируемая функция переменных х и у. Возникает вопрос о том, при каких условиях это функциональное уравнение однозначно разрешимо относительно у, т.е. однозначно определяет явную функцию y=(x), и следующий вопрос о том, при каких условиях эта явная функция непрерывна и дифференцируема.

Трудность этих вопросов видна уже на простейшем примере уравнения y² - x = 0. Это уравнение

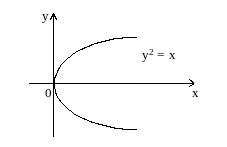
определяет при х0 бесконечно много явных функций.

Например, и любая функция, равная + для одних значений х, и - для других значений.

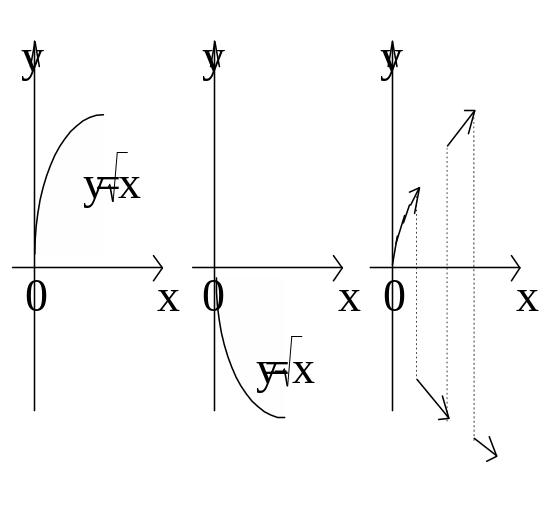
Вопрос 1. При каких условиях существует единственная явная функция, удовлетворяющая уравнению y² = x? Фиксируем точку N₀(x₀,y₀) на кривой y²-x=0, отличную от начала координат.

Очевидно, что часть кривой, лежащая в достаточно малой окрестности точки N₀, однозначно проектируется на ось Ох.

x₀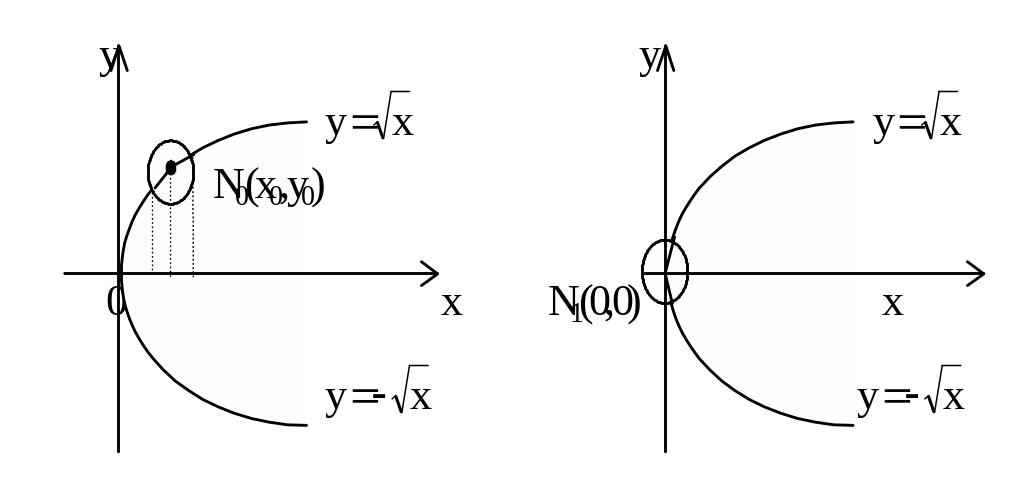

Аналитически это означает, что если рассматривать функцию f(x,y)=y² - x только в этой достаточно малой окрестности точки N₀, то уравнение f(x,y)=0 однозначно разрешимо относительно у и определяет единственную явную функцию для у₀>0 (см. рис.) и для у₀<0.

Если мы теперь рассмотрим точку N₁(0,0), то часть кривой

y²-x=0 не однозначно проектируется на ось ОХ (см. рис.). Аналитически это означает, что если рассматривать функцию f(x,y)=y²-x в любой окрестности т. N₁(0,0), то уравнение f(x,y)=y²-x=0 не является однозначно разрешимым относительно у. Заметим, что в этой точке N₁(0,0) частная производная функции f(x,y)=y²-x обращается в нуль. В общем случае это обстоятельство имеет принципиальное значение: для однозначной разрешимости уравнения f(x,y)=0 в окрестности т. (х₀,у₀) относительно у требуется, чтобы .

В случае, когда рассматривается уравнение вида F(u, x₁, ..., x_m)=0, имеют место те же трудности, что и в случае одной переменной: для однозначной разрешимости этого уравнения относительно u нужно рассматривать функцию F(u, x₁, ..., x_m) в окрестности точки (для которой , и требовать, чтобы в т. N₀.

Формулировка теоремы о неявной функции имеет вид.

Теорема. Пусть функция F(u, x₁, ..., x_m) дифференцируема в некоторой окрестности точки , причем и . Тогда для любого достаточно малого >0 существует такая окрестность точки , в которой определена (единственная) функция u=u(x₁, ..., x_m) удовлетворяющая условию u-u₀< и являющаяся решением уравнения F(u, x₁, ..., x_m)=0.

Эта функция u=u(x₁, ..., x_m) непрерывна и дифференцируема в окрестности т. М_{0 .}

Замечание 1. Частные производные вычисляются по формулам

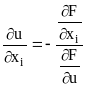(i = 1, ..., m).

Эти формулы получаются следующим образом: подставим неявную функцию u=u(x₁, ..., x_m) в уравнение F(u, x₁, ..., x_m)=0,

получим

F(u(x₁, ..., x_m), x₁, ..., x_m)=0.

Это равенство является тождеством по x₁, ..., x_m. Вычислим частные производные от обеих частей этого равенства по x_i, используя теорему о производной сложной функции,

Аналогично можно найти и высшие k-е производные неявной функции, если функция F(u, x₁, ..., x_m) дифференцируема k раз.

Пример 1. Найти частные производные функции z, заданной неявно:

F  z³ + x⁵ + y⁵ - 2xyz + 2x - 4 = 0.

Уравнение одназначно разрешимо относительно z, если , т.е. 3z² - 2xy  0.

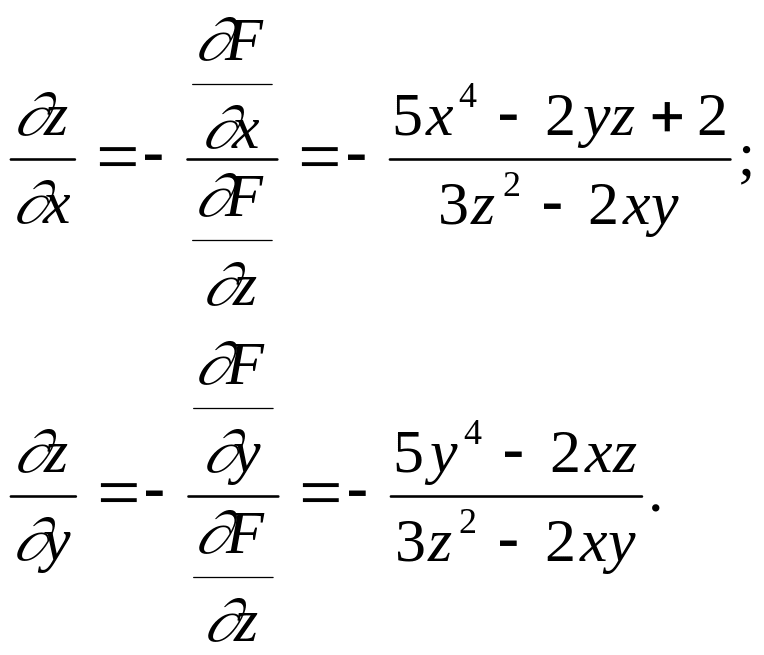
Теорема о неявной функции имеет следующие геометрические приложения.

Пусть задана поверхность уравнением F(x,y,z)=0.

Требуется написать уравнение касательной плоскости к этой поверхности и вычислить координаты нормального вектора к этой поверхности в некоторой точке (x₀,y₀,z₀). Предположим, что одна из частных производных отлична от нуля в этой точке. Это значит, что одна из переменных может быть выражена как функция двух других.

Пусть, например, , тогда x = (y,z), а для такой функции, уравнение касательной плоскости имеет вид

Нормальный вектор имеет координаты:

.

Подставляя сюда выражения для , получим

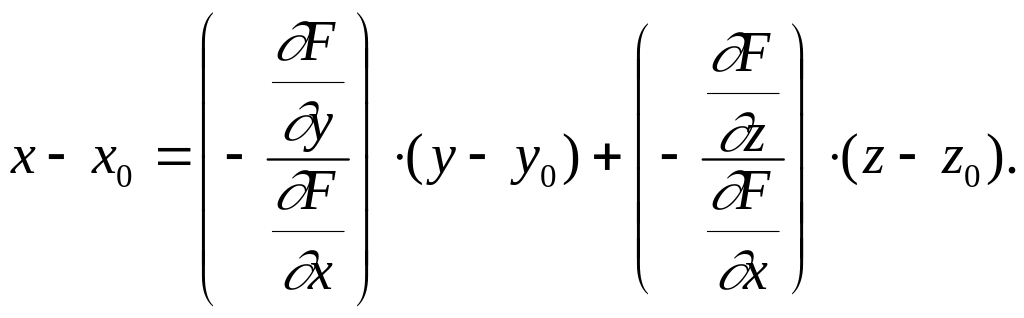
или , а в качестве нормального вектора к поверхности можем взять следующий:

.

Замечание: Если рассматривать поверхность уровня F(x,y,z)=C функции u=F(x,y,z), то мы получим, что ортогонален поверхности уровня.

Пример 2. Дана поверхность x² +4y² +2z² = 7. Написать уравнения касательных плоскостей к этой поверхности, которые параллельны плоскости x+y+z=1

Здесь F(x,y,z) = x² +4y² +2z² - 7,

.

Нормальный вектор к поверхности имеет координаты

он должен быть коллинеарен нормальному вектору к заданной плоскости, т.е. вектору .

Отсюда

Решив систему уравнений , находим координаты точек касания .

Касательные плоскости имеют уравнения: