1.9.4. Предел функции нескольких переменных

Пусть функция u=f(M) определена на множестве  R^m и т.А обладает свойством, что в любой ее окрестности есть точки из (отличные от А, если А ). Сама точка А может не принадлежать области определения функции u=f(M).

Определение предела функции нескольких переменных по своей структуре не отличается от определения предела функции одной переменной. Основное содержание его: если аргумент М мало отличается от А, то значение функции f(M) мало отличается от b (предела функции). Определения предела функции нескольких переменных по Гейне и Коши имеют вид:

Опр. 1* Число b называется пределом функции u=f(M) при МА, если для любой последовательности точек из , сходящейся к т.А

(M_n  A), соответствующая последовательность значений функции сходится к b.

Опр. 1

Число b называется пределом функции u=f(M) при МА, если для любого >0 существует такое >0, что для всех точек М , удовлетворяющих условию 0<(M,A)<, справедливо неравенство .

Замечание 1. Иногда пишут .

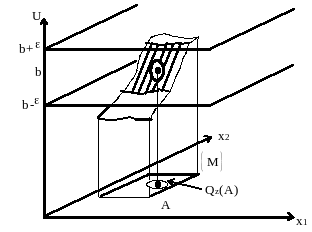
На рисунке дана иллюстрация определения предела по Коши для случая m=2. Для любого >0 существует такая проколотая -окрестность т.А, значения функции в которой отличаются от b меньше, чем на  (другими словами, график функции попадает в -полосу плоскости u=b).

Пример 1. . Проверим, что , для этого >0 надо найти такое >0, что из неравенства

Очевидно, можно положить =².

Заметим, что если существует предел функции u=f(M) при МА, то существуют пределы f(М), когда М стремится к т.А вдоль любого луча, причем все эти пределы одинаковы и совпадают с пределом функции. Следовательно, если для функции удается указать, по крайней мере, два направления, вдоль которых пределы функций различны, то предела у функции нет.

Пример 2.

Для этой функции вдоль осей Оx и Oy пределы существуют и равны 0 (на координатных осях функция равна 0), но вдоль прямой y=kx

зависит от k.

Отсюда получаем, что предела в нуле этой функции нет.

Возникает вопрос, будет ли функция нескольких переменных иметь предел, если все пределы вдоль лучей будут одинаковы? Ответ отрицательный, что видно из следующего примера.

Пример 3. Функция равна 1 на оси Ох и двух кругах радиуса 1, касающихся оси Ох в начале координат, в остальных точках она равна 0 (см. рис.)

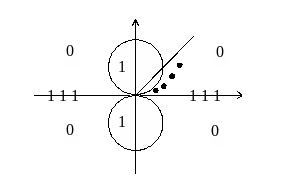
Любой луч, кроме Ох, идущий в начало координат, попадает в круг, а там функция равна 1, следовательно, предел вдоль любого луча равен 1. С другой стороны, есть последовательности точек, расположенных между осью Ох и окружностью , сходящиеся к нулю, вдоль которых функция равна 0, и, следовательно, предел ее вдоль таких последовательностей равен нулю. Отсюда получаем, что предела в нуле функция не имеет.

Аналогично одномерному случаю можно дать определение предела функции при М  (при этом должно быть не ограниченным).

Определение 2.

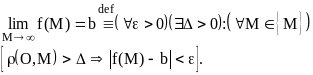
Пример 4. . Запишем определение предела

.

Из неравенства ( < 1), получаем

.

Отсюда очевидно, что можно положить .

Замечание 2. Для пределов суммы, разности, произведения и частного функций нескольких переменных справедливы те же формулы, что и в одномерном случае.