1.2.4.2. Полярное уравнение кривой второго порядка

Пользуясь общим свойством эллипсов, гипербол и парабол, выведем общее уравнение этих кривых второго порядка в полярных координатах при некотором специальном выборе полярной системы координат.

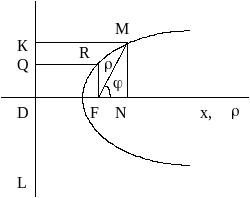
Пусть дана произвольная из указанных линий (эллипс, ветвь гиперболы или парабола). Возьмем фокус F кривой (любой, если их два) и соответствующую ему директрису L (если рассматривается ветвь гиперболы, то берется фокус и директриса, ближайшие к этой ветви).

Введем полярную систему координат так, чтобы полюс О совпал с фокусом F, а полярная ось была направлена по оси симметрии кривой в сторону, противоположную директрисе L.

Возьмем на кривой произвольную точку М(;), соединим ее отрезком FM с фокусом и опустим перпендикуляр МК на директрису. Кроме того, из точки F проведем перпендикуляр FR к полярной оси до пересечения с кривой в точке R, а из точки R опустим перпендикуляр RQ на директрису (Рис. 12).

Обозначим FR=p и будем называть это число фокальным параметром. На основании общего свойства кривых второго порядка По тем же соображениям: или , откуда

Подставим найденные выражения для FM и КМ в равенство , получим:

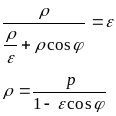(3)

Уравнение (3) называется уравнением кривой второго порядка в полярных координатах. При <1 кривая является эллипсом, при >1 - ветвью гипиерболы, при =1 - параболой.

Фокальный параметр Р из уравнения параболы определяется непосредственно. Для того, чтобы фокальный параметр выразить через параметры эллипса и гиперболы, следует заметить, что фокальный параметр Р является ординатой точки кривой, абсцисса которой равна абсциссе соответствующего фокуса (в выбранной при выведении канонического уравнения соответствующей кривой системе ХОY).

Подставляя вместо координат точки М(х;у) в уравнение эллипса координаты точки (-с;р), получим:

или ,

откуда следует

Аналогично, подставляя в уравнение гиперболы координаты точки (с;р), получим:

или ,

откуда следует соотношение

.

Рассмотрим несколько задач на кривые второго порядка:

Задача 1.

Дано уравнение гиперболы 16х²-9у²=144. Найти длины ее осей, координаты фокусов, эксцентриситет; составить уравнения директрис и асимптот гиперболы.

Решение.

Приведем уравнение гиперболы к каноническому виду и определим как параметры гиперболы, так и расстояние с от начала координат до фокуса:

или ,

откуда а=3, b=4, , эксцентриситет = .

Действительная ось 2а=6; мнимая ось 2b=8.

Уравнения директрис: .

Уравнения асимптот: .

Задача 2.

Составить уравнение эллипса, симметричного относительно координатных осей, зная, что он проходит через точки М₁(2;3) и М₂ .

Решение.

Учитывая симметричность эллипса относительно осей координат, его каноническое уравнение будет иметь вид: и вместо текущих координат подставим в это уравнение сначала координаты точки М₁, а затем координаты точки М₂. Из получившейся системы уравнений:

определим параметры эллипса а и b.

Обозначив

, ,

получим следующую систему уравнений:

.

Решая ее, получим, что:

,

откуда а²=16, b²=12.

Следовательно, искомое уравнение эллипса будет:

.

Задача 3.

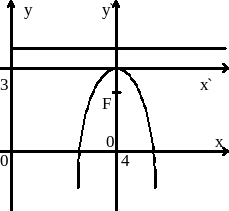
Найти вершину, фокус, ось и директрису параболы

у = -2х² +16х-29.

Решение.

Преобразуем данное уравнение следующим образом:

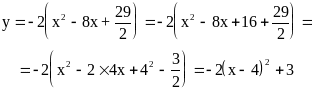
Отсюда .

Обозначив х`= х-4 и у`= у-3, перейдем к новой системе координат O`x`y`, начало которой находится в точке O`(4;3), а оси O`x` и O`y` сонаправлены с осями Ох и Оу. В результате получим простейшее уравнение данной параболы

’.

Отсюда , то есть . Итак, вершина параболы находится в точке O`(4;3); координаты фокуса

x_F = x_O` = 4;

то есть F ; уравнение оси параболы x = x_O` = 4, то есть х-4=0; уравнение директрисы , то есть 8y-25=0.

Задача 4.

Уравнение эллипса привести в полярной системе координат к уравнению вида

.

Решение:

Найдем из данного уравнения параметры a, b, c, затем найдем эксцентриситет и фокальный параметр эллипса :

а²=4, b²=3, c²=1, , .

Искомое уравнение будет иметь вид:

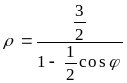или .

Задача 5.

Данное уравнение кривой в полярных координатах

Привести его к каноническому уравнению в прямоугольных координатах.

Решение.

В данном уравнении , . Так как эксцентриситет >1, то данное уравнение является уравнением гиперболы, у которой b²=c²-a². Таким образом, данные параметры могут быть записаны в виде системы двух уравнений

Из этой системы находим, что а=1, с=3, b²=8. Следовательно, уравнение гиперболы имеет вид:

.

52