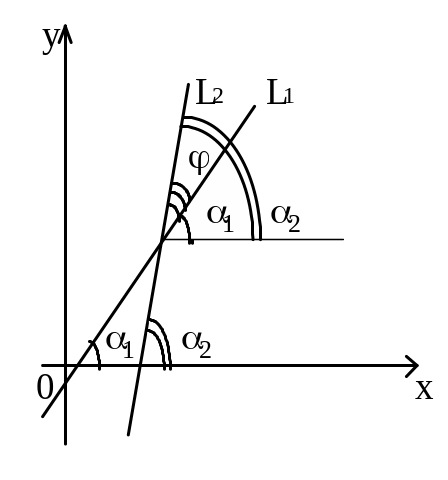1.1.5.3. Уравнение прямой в отрезках

Рассмотрим полное (все коэффициенты A, B и C отличны от нуля) уравнение прямой

.

Его можно записать в виде (т.к. )

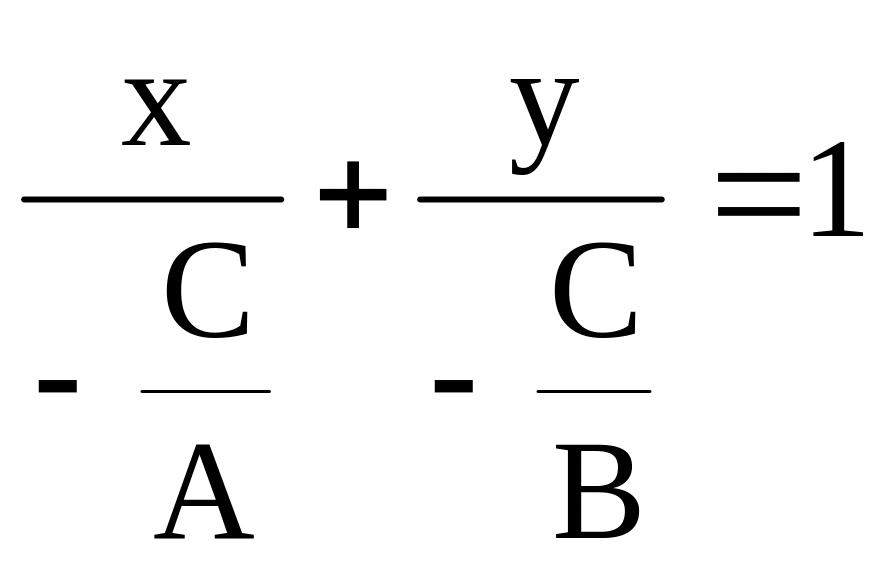
и затем положить . Получим .

Последнее уравнение называется уравнением прямой “в отрезках”. Числа a и b равны соответственно величинам отрезков, отсекаемых прямой на осях Ox и Oy соответственно.

1.1.5.4. Каноническое уравнение прямой

Любой ненулевой вектор, параллельный данной прямой, назовем направляющим вектором этой прямой.

Найдем уравнение прямой, проходящей через данную точку и имеющей заданный направляющий вектор .

Точка лежит на указанной прямой тогда и только тогда, когда векторы коллинеарны, т.е. когда их координаты пропорциональны

(6.5)

Это уравнение обычно называют каноническим уравнением прямой.

В уравнении (6.5) одно из чисел l или m может равняться нулю, т.к. это есть координаты вектора. например, уравнение оси Ox запишется так .

1.1.5.5. Параметрические уравнения прямой

Примем за параметр t величину, стоящую в правой и левой частях соотношения (6.5), .

Получим или

Это и есть искомые параметрические уравнения прямой.

1.1.5.6. Угол между двумя прямыми. Условия параллельности и перпендикулярности двух прямых

1). Пусть прямые L₁ и L₂ заданы общими уравнениями

.

Задача об определении угла между прямыми сводится к определению угла между нормальными векторами этих прямых:

(6.6)

Условие параллельности прямых L₁ и L₂ эквивалентно коллинеарности их нормальных векторов :

.

Условие перпендикулярности прямых L₁ и L₂ получаем из формулы (6.6) при cos:

.

2). Если прямые L₁ и L₂ заданы каноническими уравнениями

,

то рассматривая их направляющие векторы , аналогично случаю 1). имеем:

(6.7)

Условие параллельности прямых L₁ и L₂ :

.

Условие перпендикулярности прямых L₁ и L₂ :

3). Пусть прямые L₁ и L₂ заданы уравнениями с угловым коэффициентом .

Здесь - углы наклона прямых L1 и L2 к оси Ox, а - один из углов между этими прямыми. Из рисунка видно, что .

Отсюда

.

Т.е. угол между прямыми L₁ и L₂ определяется по формуле:

(6.8)

Если в этой формуле поменять местами k₁ и k₂ , то формула определит нам угол между прямыми, смежный к прежнему углу. Т.к. эти два угла в сумме равны  и их тангенсы отличаются только знаком.

Прямые параллельны, если tg, т.е. k₁=k₂ .

Условие перпендикулярности прямых L₁ и L₂ получим из формулы (6.8), т.к. tg не существует при .

Условие перпендикулярности прямых L₁ и L₂ запишем в виде:

.

1.1.5.7. Нормированное уравнение прямой. Отклонение точки от прямой

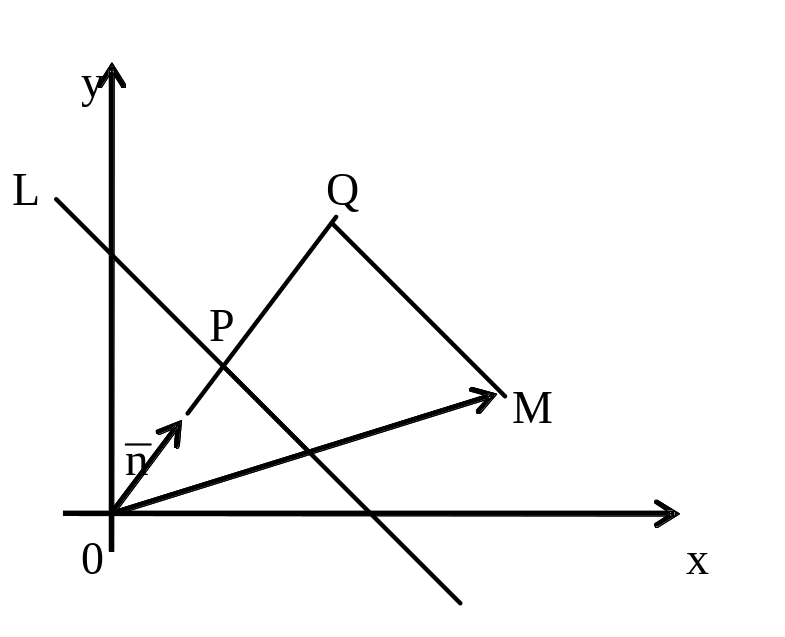
Рассмотрим произвольную пря- мую L. Через начало координат O проведем прямую n, перпендику- лярную L, и обозначим через P точку пересечения этих прямых.

На прямой n возьмем единичный вектор , направление которого совпадает с направлением отрезка (если точки O и P совпадают, то направление вектора выбираем произвольно).

Выразим уравнение прямой L через два параметра:

1) длину p отрезка и

2) угол  между вектором и осью Ox.

Вектор - единичный, следовательно его можно записать в виде

(6.9)

Точка лежит на прямой L тогда и только тогда, когда проекция вектора на ось, определяемую вектором , равна p:

. (6.10)

В силу определения 2 скалярного произведения, учитывая, что имеем:

. (6.11)

Учитывая, что и равенство (6.9), получим

(6.12)

Из соотношений (6.9), (6.10) и (6.11) получаем, что точка лежит на прямой L тогда и только тогда, когда ее координаты удовлетворяют уравнению

(6.13)

Это уравнение называется нормированным уравнением прямой.

Пусть число d обозначает расстояние от точки M до прямой L.

Определение. Отклонением  точки M от прямой L называется число +d в случае, когда точка M и начало координат O лежат по разные стороны от прямой L, и число -d в случае, когда точки M и О лежат по одну сторону от прямой L. Если же начало координат О лежит на прямой L, положим отклонение равным +d в случае, когда точка М лежит по ту сторону от прямой L, куда направлен вектор , и равным -d в противоположном случае.

Теорема. Геометрический смысл левой части уравнения (6.13) состоит в том, что левая часть этого уравнения равна отклонению точки от прямой L, определяемой уравнением (6.13).

Доказательство.

Спроектируем точку М на ось, определяемую вектором , обозначим эту проекцию Q. Отклонение  точки М от прямой L равно PQ, где PQ обозначает величину направленного отрезка оси, определяемой вектором .

Из рисунка видно, что

, (6.14)

но , а в силу (6.11) и (6.12) получаем

.

Из последнего равенства и (6.14) имеем

.

Отсюда получаем возможность находить расстояние от точки до прямой L:

.