7.2 Реализация в программе MathCad. Метод наименьших квадратов
метод
наименьших квадратов.
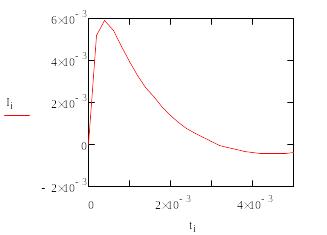
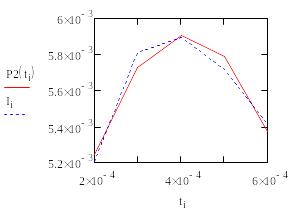
Рисунок
11 - График зависимости силы тока от
времени
На
первом участке
Вычисление
коэффициентов линейной регрессии
Полином
второй степени
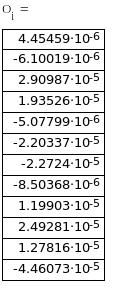
Вычисление
ошибок аппроксимации
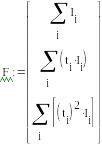
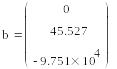
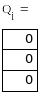
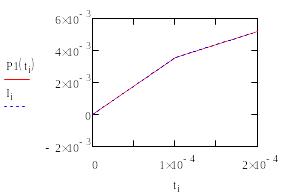
Рисунок
12 - График ошибок аппроксимации на 1-ом
участке
На
втором участке
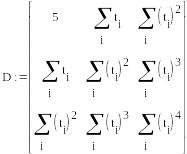
Вычисление
коэффициентов линейной регрессии
Полином
второй степени
Вычисление
ошибок аппроксимации
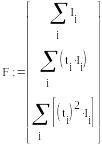
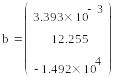
Рисунок
13 - График ошибок аппроксимации на 2-ом
участке
На
третьем участке
Вычисление
коэффициентов линейной регрессии
Полином
третьей степени
Вычисление
ошибок аппроксимации
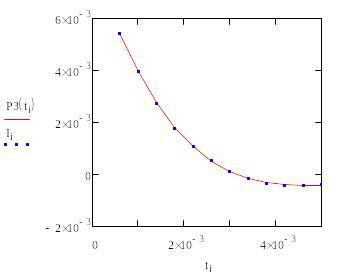
Рисунок
14 - График ошибок аппроксимации на 3-ом
участке
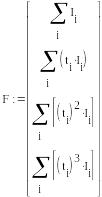
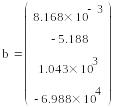
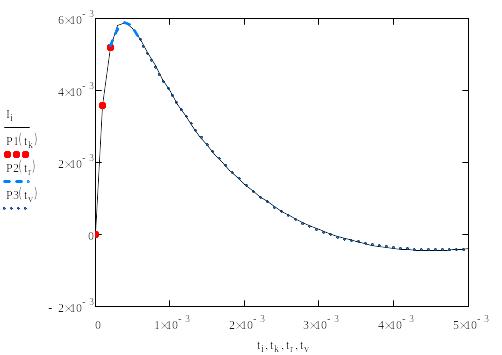
Рисунок 15 - График ошибок аппроксимации на трех участках
Анализ результатов.
Решение
задачи аппроксимации было проведено в
программе MathCad
методом наименьших квадратов и в пакете
Excel
с использованием мастера диаграмм с
выводом уравнения линии тренда. Результаты
двух программ совпадают. Получена
аналитическая формула зависимости силы
тока от времени на интервале
.
8 Численное интегрирование
8.1 Реализация в программе С++. Метод левых прямоугольников.
8.1.1 Блок-схема
Да
Нет
I=45.527*t
–97510*t*t
93642000*t*t
Нет
Да
I=0.003393+12.255*t - 14920*t*t
I=0.008168–5.188*t+1043*t*t–69880*t*t*t
Рисунок 16 - Блок-схема. Метод левых прямоугольников
8.1.2 Код программы
#include<iostream.h>
#include<math.h>
int main()
{double R4=1.88, y,t1=0,t2=0.005,h,ILev,t=0,S=0,Q,I;
int n=200,j;
h=(t2-t1)/200;
for(j=0;j<=199;j++)
{t=t1+h*j;
{if(t<0.0002) y=45.527*t-97510*t*t;
if((t>0.0002) && (t<0.0006)) y=0.003393+12.255*t-14920*t*t;
else y=0.008168-5.188*t+1043*t*t-69880*t*t*t;
S=S+pow(y,2);}
ILev=h*S;}
Q=R4*ILev;
cout<<"ILev="<<ILev<<"\t"<<"Q="<<Q<<endl;
return 0;}
Таблица 5.Результат работы в программе С++
