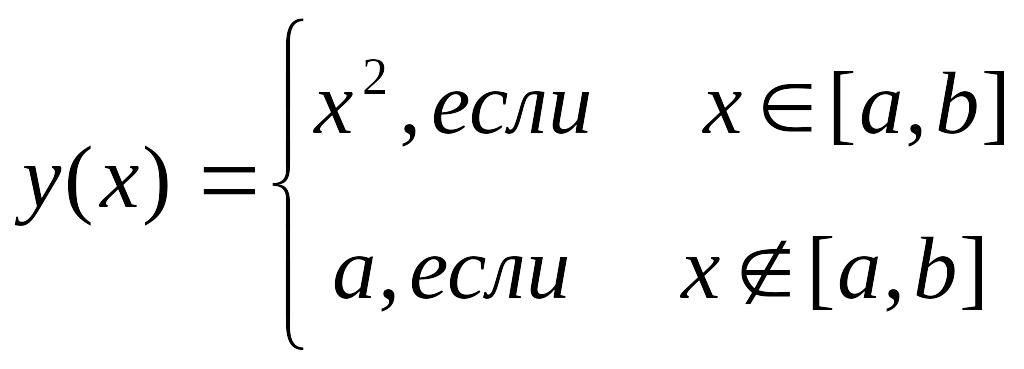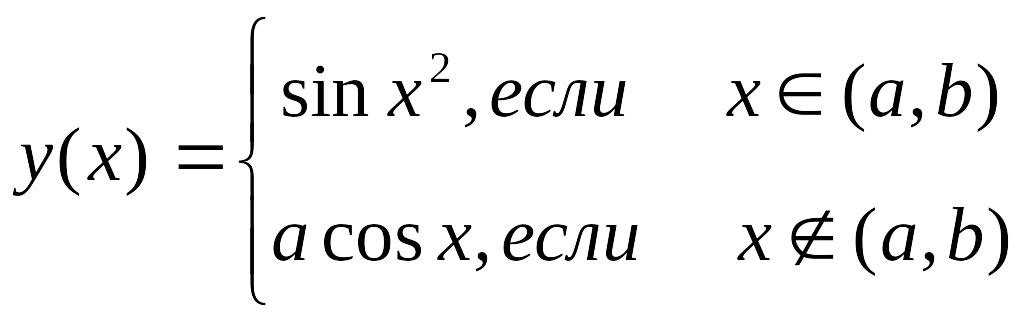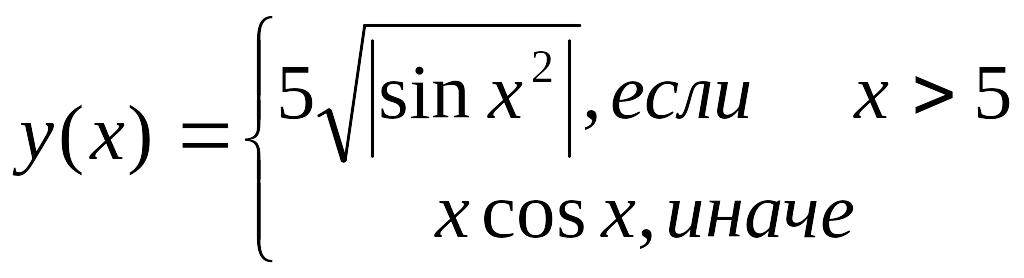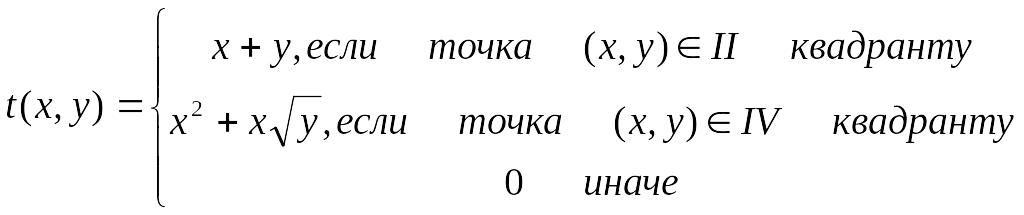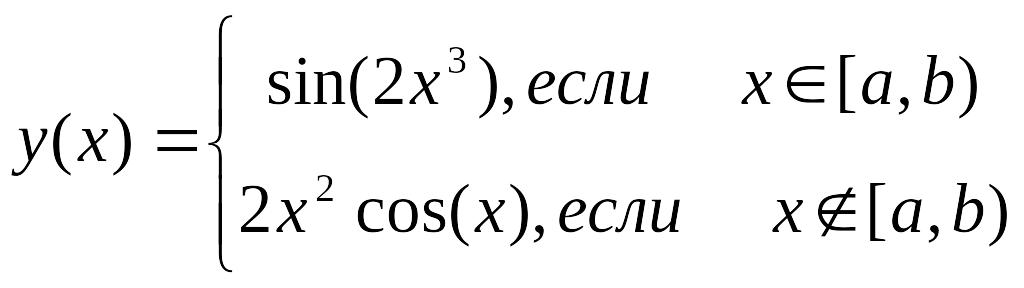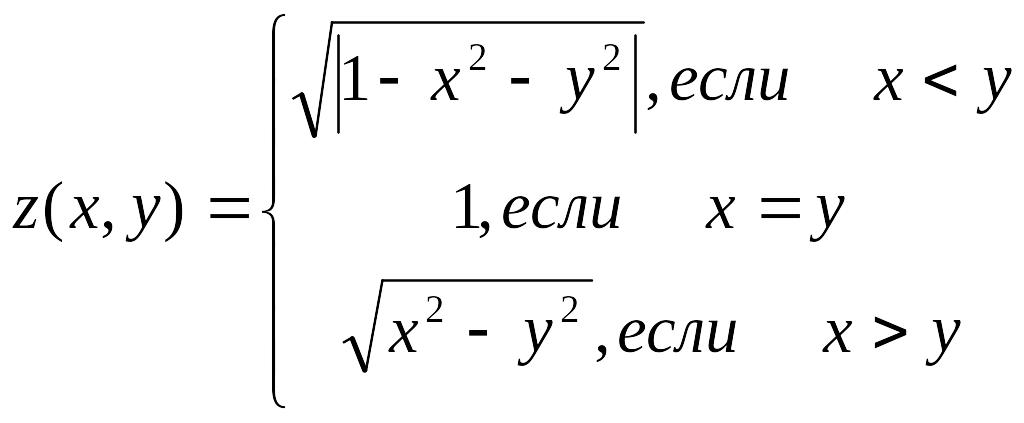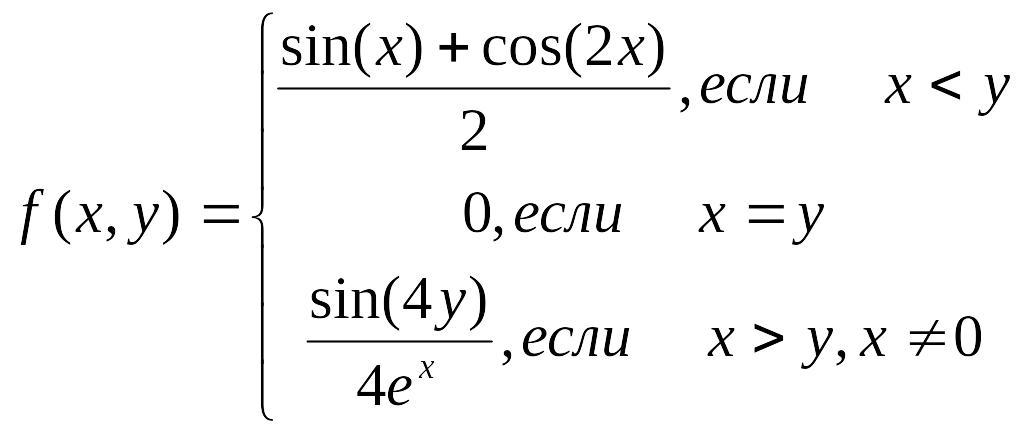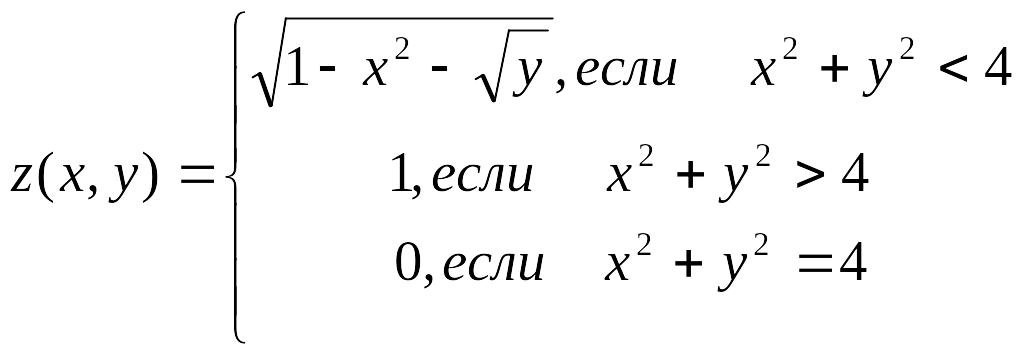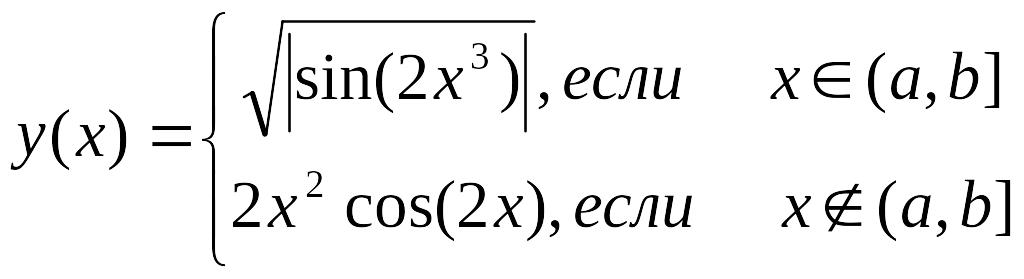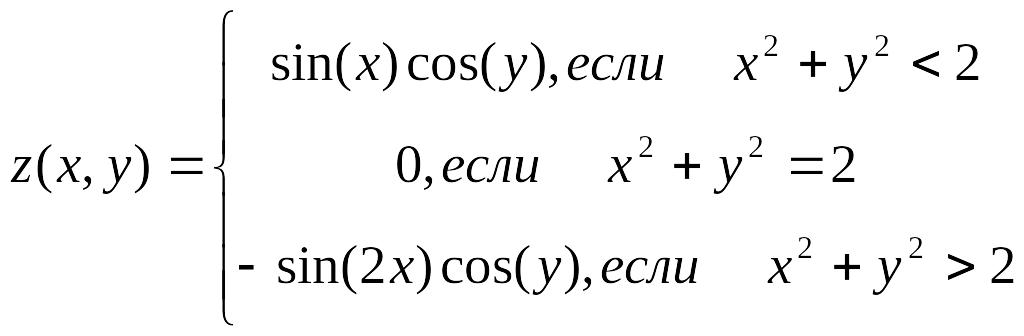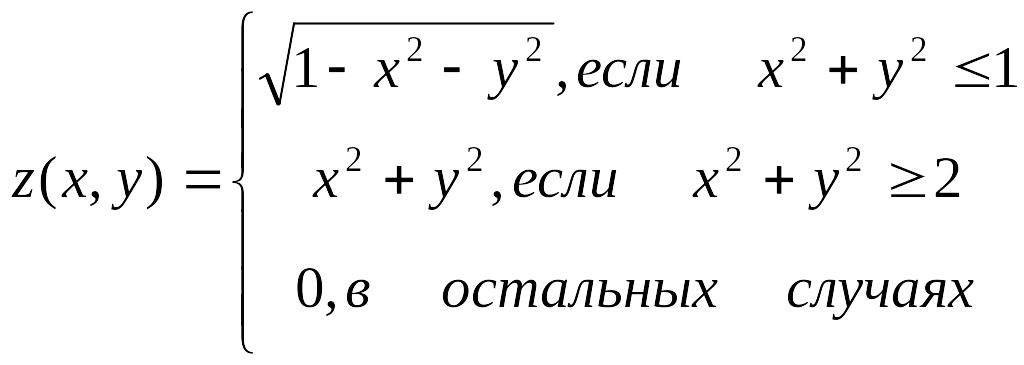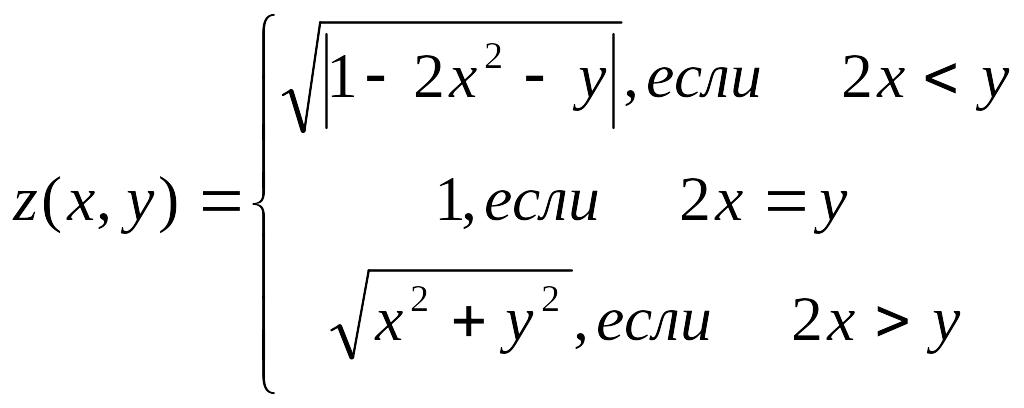Задание №2 Применение логических функций Задание 2.1 Решение квадратного уравнения
На
листе
2
(“Задание 2a” цвет ярлыка - красный)
реализовать в электронной таблице схему
решения квадратного уравнения вида
Вычислить значение дискриминанта
.
В зависимости от значения дискриминанта,
используя функцию ЕСЛИ(),
вычислить значения действительных
корней уравнения. Для обозначения
коэффициентов, дискриминанта и корней
уравнения использовать именные
ячейки.
Реализовать проверку найденных корней,
используя логические функции ЕСЛИ() и
И(). Тестовые значения параметров задавать
произвольно.
Порядок выполнения задания:
В ячейки A3, В3 и С3 введем значения коэффициентов квадратного уравнения и обозначим эти ячейки именами a, b и с;
Ячейку, где будет размещаться значение дискриминанта, обозначим именем D. Для вычисления дискриминанта введем формулу =b^2-4*a*c;
Для вычисления первого корня x1 введем функцию ЕСЛИ с соответствующим условием для d (d>0) и формулой для первого корня уравнения (-b+КОРЕНЬ(D))/(2*a), а в противном случае выдать замечание: «Действительных корней НЕТ»;
Для вычисления второго корня x2 введем функцию ЕСЛИ с соответствующим условием для d (d>0) и формулой для второго корня уравнения (-b-КОРЕНЬ(D))/(2*a), в противном случае выдать замечание: «Действительных корней НЕТ»;
Пример: =ЕСЛИ(d>0;(-b+КОРЕНЬ(d))/(2*a);"Нет решения")
Выполнить проверку найденных корней, используя логические функции ЕСЛИ() и И()
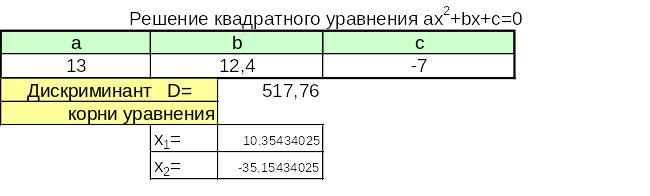
Вид электронной таблицы может иметь следующий вид:
Задание 2.2 с помощью логических функций вычислить значения заданной функции
На рабочем листе 3 (название “Задание 2b” цвет ярлыка - желтый). Используя математические, логические и статистические функции Excel, вычислить таблицу значений функции, указанной в таблице. С помощью формул подсчитать:
сумму и количество положительных значений функции (использовать функции СЧЕТЕСЛИ(); СУММАЕСЛИ() );
сумму и количество отрицательных значений функции;
минимальное и максимальное значения функции на области определения.
Замечание: Формат функций СЧЕТЕСЛИ(); СУММАЕСЛИ()
СЧЕТЕСЛИ(диапазон; “условие”) – подсчитывает количество непустых ячеек, удовлетворяющих заданному условию
Например: =СЧЁТЕСЛИ(B3:K12;"=2") подсчитывает в заданном диапазоне количество ячеек, в которых находится значение равное 2.
СУММЕСЛИ(диапазон; “условие”; [диапазон_суммирования]) - cуммирует ячейки, заданные критерием.
Диапазон - диапазон вычисляемых ячеек.
Критерий - критерий в форме числа, выражения или текста, определяющего суммируемые ячейки. Например, критерий может быть выражен как 32, "32", ">32", "яблоки".
Диапазон_суммирования — необязательный параметр, фактические ячейки для суммирования.
Ячейки в «диапазон_суммирования» суммируются, только если соответствующие им ячейки в аргументе «диапазон» удовлетворяют критерию. Если «диапазон_суммирования» опущен, то суммируются ячейки в аргументе «диапазон».
Таблица № 3 Индивидуальные задания
№ варианта |
Вычисляемая функция |
Значения аргументов и параметров |
|
|
|
a=0, b=1 x=-1,0.5,…,2 |
|
|
|
a= -2, b= 2 x=-4,-3.5,…,4 |
|
|
|
x=-10,..10 шаг 1 |
|
|
|
x=-1,0,1, y=-2,-1,…,2 |
|
|
|
x,y меняются от -3 до 3 с шагом 0,25 |
|
|
|
x,y меняются от 1 до 6 с шагом 0,5 |
|
|
|
a=-1, b=1 x=-3,-2,…,3 |
|
|
|
x,y меняются от -4 до 3 с шагом 0,25 |
|
|
|
|
|
|
|
x,y меняются от -2 до 3 с шагом 0,25 |
|
|
|
|
|
|
|
a=-3, b=4 x=-3,-2.5,…,3 |
|
|
|
x, y меняются от -3 до 3 с шагом 0,25 |
|
|
|
|
|
|
|
, шаг по x и по y 0,25 |
,
шаг по x, y
равен 0.1
,
шаг по x и по y
0,25
,
шаг по x и по y
0,25