6 Анализ характеристик каналов с интеграцией речи и данных

Для решения этой задачи нам потребуется новый математический аппарат, краткое изложение которого дается в следующем разделе.

6.1 Метод производящих функций

Этот метод является применением известного вам по теории обработки сигналов z-преобразования к описанию распределения вероятностей.

Пусть имеется функция дискретного аргумента n , представляющая собой невозрастающую последовательность. Z-преобразованием последовательности называют функцию комплексной переменной

.

Если функция p_n имеет смысл распределения вероятностей полной системы событий, то соответствующее z-преобразование называют производящей функцией. Применение этого преобразования позволяет упростить решение уравнений равновесия для процессов гибели-размножения, сводя решение систем разностных уравнений к системам алгебраических.

Будем опираться на известные свойства z – преобразований, приведенные, например, в книге Л. Клейнрок «Теория массового обслуживания».

Для производящих функций нетрудно получить как частный случай следующие соотношения

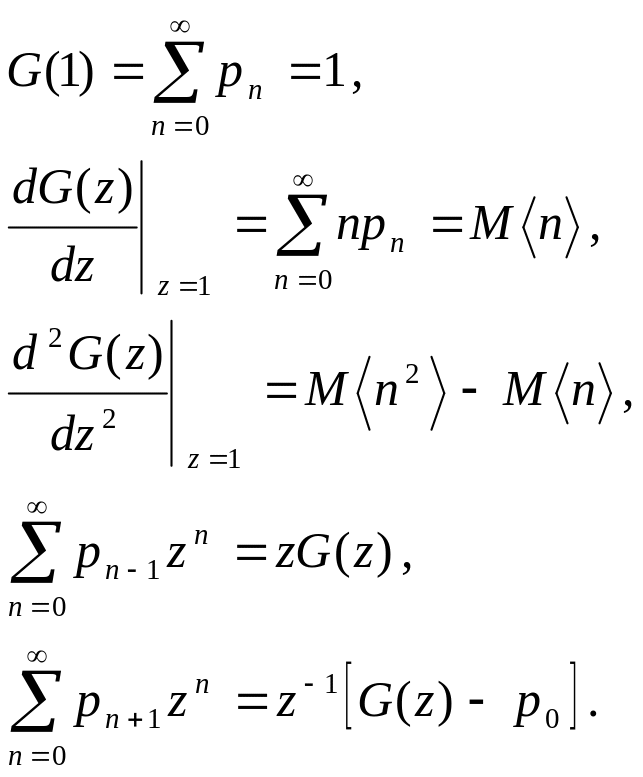
Теперь вернемся к системе массового обслуживания M/M/1, уравнения которой имеют вид

Решим эти уравнения методом производящих функций. Умножим правую и левую часть на zⁿ и просуммируем от нуля до бесконечности.

В результате получим

.

Группируя соответствующие члены, получаем

Из соотношения

Полученное выражение сразу позволяет найти среднюю длину очереди, исходя из свойств производящей функции

.

Этот результат, конечно, совпадает с полученным ранее прямым методом.

Найденная производящая функция позволяет сразу определить и все значения ве­роятностей. С этой целью можно воспользоваться таблицей z-преобразований или разложить производящую функцию в степенной ряд и выписать полученные коэф­фициенты. Можно также воспользоваться вычислением обратного z-преобразова­ния с помощью теоремы о вычетах.

.

Рассмотрим теперь систему M/M/2, которая встретится нам в дальнейшем еще раз. Решение уравнения равновесия для неё было найдено в виде

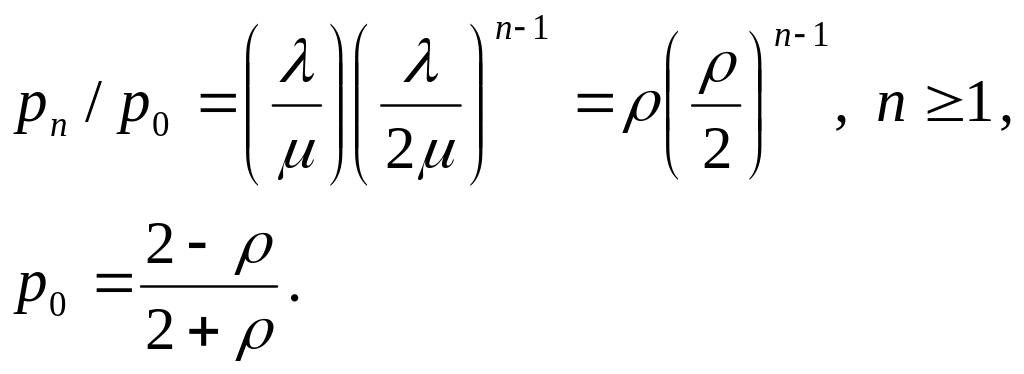
Найдем производящую функцию

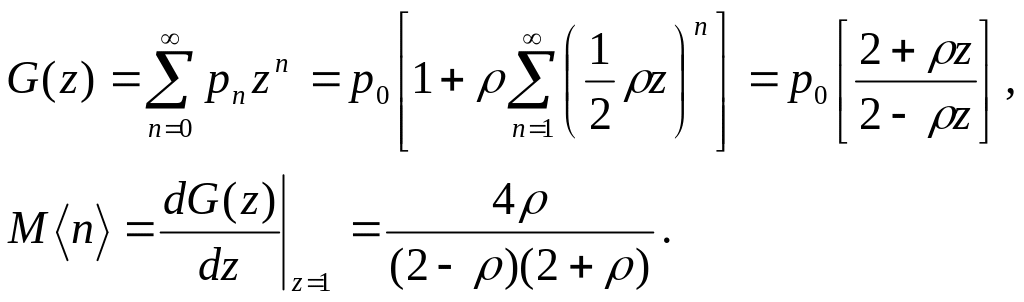
Выражения для полученных здесь производящих функций будут использованы далее при рассмотрении сетей с интеграцией средств коммутации пакетов и каналов.

6.2 Модели интеграции речи и данных.

Рассмотрим объединение двух видов нагрузки – обслуживание с коммутацией каналов, кратко – речь и нагрузка, требующая обслуживания с коммутацией пакетов – данные.

Назовем первую из этих видов нагрузка 1-го класса. Будем считать, что интенсивность поступлений ВЫЗОВОВ (требований на соединение) λ₁ а среднее время занятия 1/μ₁. Этот тип нагрузки требует одного временного канала и при отсутствии свободных каналов – блокируется.

Второй из видов нагрузки назовем Нагрузка 2-го класса. Интенсивность поступлений ПАКЕТОВ положим равной λ₂, а средняя длина пакета определяет время обслуживания 1/μ₂. Эта группа заявок ставится в очередь при отсутствии свободных каналов. В этом и состоит основное отличие двух классов нагрузки с точки зрения теории телетрафика.

Для обслуживания нагрузки в зависимости от класса может быть выделено фиксированное или переменное число каналов. В зависимости от способа предоставления каналов для заявок разного класса будет получаться различное качество обслуживания нагрузки. Наша задача проанализировать различные методы обслуживания.