Домашнее задание № 1. Вариант№1 Задача№1
Электрон
начальной скоростью которого можно
пренебречь, прошел ускоряющую разность
потенциалов U.
Найти длину волны де Бройля
![]() для двух случаев:
для двух случаев:
1. U1=51B 2. U2=510 KB.
Решение.
Длина волны де Бройля частицы зависит от импульса P.
![]()
Когда
T<<E0
, где T=Ek![]() ,
нерелятивистская частица. E0=m0c2=0.51
Мэв.
,
нерелятивистская частица. E0=m0c2=0.51
Мэв.
![]() ;
;
![]()
Когда
T![]() E0
– релятивистская частица.
E0
– релятивистская частица.

1)
![]() эв=0,51*10-4
Мэв
эв=0,51*10-4
Мэв
![]()
![]()
![]() ,
,
где
![]() м
– комптоновская длина волны.
м
– комптоновская длина волны.
![]() м=172
пм
м=172
пм
2)
![]() Кэв=0,51Мэв=
E0
Кэв=0,51Мэв=
E0
![]() Мэв=
Мэв=![]() ;
;
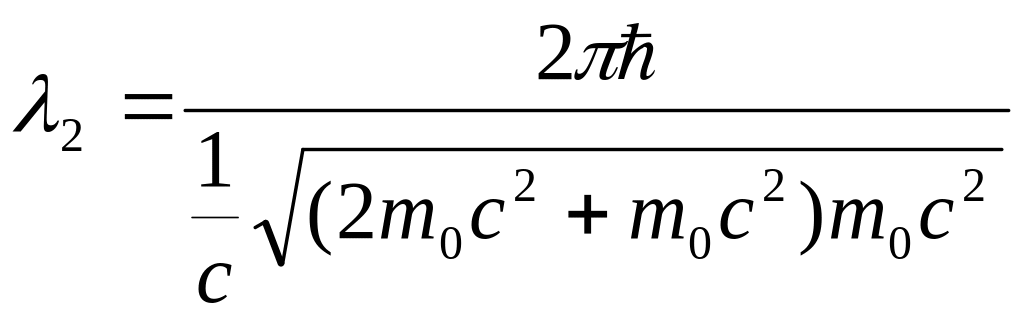
![]() м=1,4нм
м=1,4нм
Задача №2
Электрон находится в бесконечно глубоком одномерном прямоугольном потенциальном ящике шириной l. Вычислить вероятность того, что электрон, находящийся в возбужденном состоянии (n=2), будет обнаружен в средней трети ящика.
Решение.
W= (1).
(1).
![]() -
нормированная волновая функция.
-
нормированная волновая функция.
![]() .
Возбужденное состояние n=2
,
.
Возбужденное состояние n=2
,
![]() (2)
(2)
 (3), где
(3), где
![]() и
и
![]()
![]()

![]()
y(0)=0
y(![]() )=0
x
)=0
x
0
![]()
![]()
 =
=
=![]() ;
(
;
(![]() )
)
![]()
Задача №3
Рентгеновское
излучение (![]() =1нм) рассеивается электронами, которые
можно считать практически свободными.
Определить максимальную длину волны
=1нм) рассеивается электронами, которые
можно считать практически свободными.
Определить максимальную длину волны
![]() рентгеновского
излучения в рассеянном пучке.
рентгеновского
излучения в рассеянном пучке.
Решение
![]() ,
где
,
где
![]() .
.
![]() -
комптоновская длина волны.
-
комптоновская длина волны.
![]() м
м
![]()
![]()
Если
![]() =1,
то
=1,
то
![]()
![]() нм
нм
Задача №4
Определить
среднее значение координаты
![]() линейного гармонического осциллятора
в нормальном состоянии. Нормированная
волновая функция этого состояния
известна:
линейного гармонического осциллятора
в нормальном состоянии. Нормированная
волновая функция этого состояния
известна:
 ,
где a=
,
где a=![]() .
.
Решение
![]() .
.
Все
интегралы вида
![]() , вследствие нечетности подынтегральной
функции
, вследствие нечетности подынтегральной
функции
Вариант №2
Задача №1
На
узкую щель шириной а=1мкм направлен
параллельный пучок электронов, имеющих
скорость
![]() =3,65 Мм/с. Учитывая волновые свойства
электронов, определить расстояние х
между двумя максимумами интенсивности
первого порядка в дифракционной картине,
полученной на экране, отстоящем на L=10
см от щели.
=3,65 Мм/с. Учитывая волновые свойства
электронов, определить расстояние х
между двумя максимумами интенсивности
первого порядка в дифракционной картине,
полученной на экране, отстоящем на L=10
см от щели.
Решение
Для
максимумов первого порядка (k=1)
угол
|
a
Ltg
X |
Задача №2
Многоэнергетический поток электронов (Е=100эв) падает на низкий прямоугольный потенциальный барьер бесконечной ширины. Определить высоту потенциального барьера U, если известно, что 4% падающих на барьер электронов отражается.
Решение
![]() ,
в области I
кинетическая энергия электрона равна
Е.
,
в области I
кинетическая энергия электрона равна
Е.
![]() т.к.
т.к.
![]() .
.
![]()
![]() Разделим числитель
и знаменатель дроби и знаменатель дроби
Разделим числитель
и знаменатель дроби и знаменатель дроби
![]() :
:
 .
Возведя обе части равенства в квадрат,
найдем высоту потенциального барьера:
.
Возведя обе части равенства в квадрат,
найдем высоту потенциального барьера:
 эв.
эв.
Задача№3
Определить
максимальную скорость
![]() фотоэлектронов,
вырываемых с поверхности серебра:
1)ультрафиолетовым излучением с длиной
волны
фотоэлектронов,
вырываемых с поверхности серебра:
1)ультрафиолетовым излучением с длиной
волны
![]() =0,155мкм
=0,155мкм
2)
![]() -излучением
с длиной волны
-излучением
с длиной волны
![]() =1пм.
=1пм.
Решение
![]() ;
;
![]() .
.
если
 ,
то классический случай.
,
то классический случай.
![]() Дж=1,28*10-18
ДЖ
Дж=1,28*10-18
ДЖ
![]() эв=8эв.
Е0=0,51Мэв.
эв=8эв.
Е0=0,51Мэв.
;
![]() А=
4,7эв . А=4,7*1,6*10-19Дж=7,52*10-19Дж.
А=
4,7эв . А=4,7*1,6*10-19Дж=7,52*10-19Дж.
![]() м/с
м/с
2)![]() Дж
Дж
![]() эв=1,24*106эв
=1,24Мэв
эв=1,24*106эв
=1,24Мэв
![]() .
Работа выхода А=4,7эв, мала по сравнению
с энергией фотона, поэтому можно принять,
что максимальная кинетическая энергия
электрона равна энергии фотона:
.
Работа выхода А=4,7эв, мала по сравнению
с энергией фотона, поэтому можно принять,
что максимальная кинетическая энергия
электрона равна энергии фотона:
![]() Мэв
.
Мэв
.
Но для вычисления скорости нужно взять релятивистскую формулу кинетической энергии:
![]()
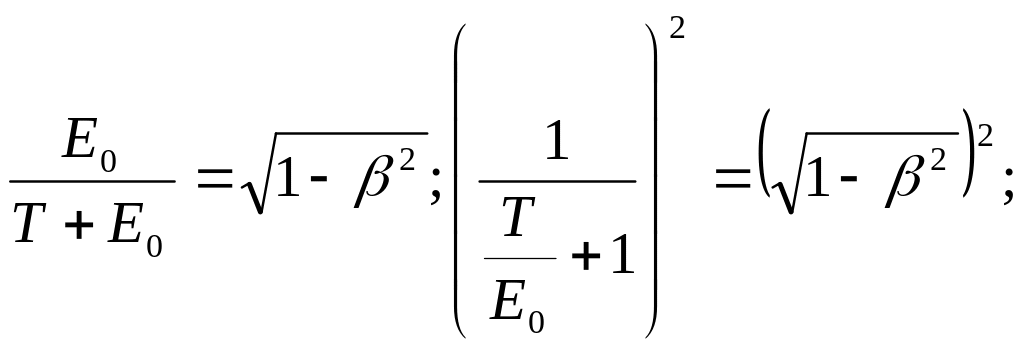



![]() , где
, где
![]() и
и
![]()
![]()
![]() м/c
=2,85*108
м/c
м/c
=2,85*108
м/c