Тема 2. Постановка задач статистической теории распространения волн.

План проведения занятий по теме:

• Закрепление теоретических навыков по теме «Введение в теорию случайных функций»;

• Исследование свойств случайного однородного поля и его спектральных амплитуд методами статистической теории;

• Развитие памяти и творческого мышления;

• Контроль знаний, умений и навыков студентов, который проводится в ходе занятия при оценке ответов у доски и во время устного опроса;

• По итогам занятия производится выдача задания для самостоятельной работы.

Вопросы и задания

Задача 1. Найти общий вид функции корреляции изотропного, однородного и стационарного скалярного волнового поля.

Решение. Лучевая интенсивность для изотропного поляне зависит от направления: 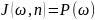, так что корреляционная функция (2.26) выражается однократным интегралом:

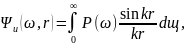
поскольку

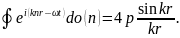
Задача 2. Выразить среднюю плотность электромагнитной энергии и средний вектор Пойнтинга в вакууме через матрицу лучевых интенсивностей 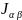, которая вводится аналогично (2.25):

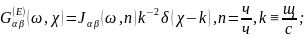
при этом, подобно (2.26),

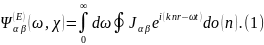
Здесь 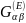— матрица спектральных плотностей, представляющая собой преоб­разование Фурье корреляционной матрицы свободного статистически однород­ного электромагнитного поля

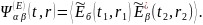
Решение. Рассматривая случай стационарного и однородного электромагнитного поля с нулевым средним значением и учитывая, что в вакууме | Н |² = |Е |². имеем

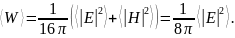
Но при 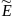= 0 в силу (1)

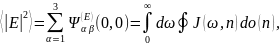
где введена лучевая интенсивность

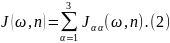
В результате имеем

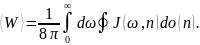
Среднее значение вектора Пойнтинга

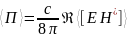
можно получить, используя спектральные разложения для Е и Н соотно­шение :

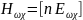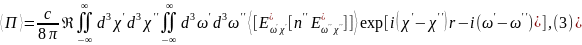
где 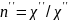. Раскрывая двойное векторное произведение, получаем выра­жение

.

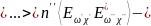Вследствие дельта-корреляции спектральных амплитуд вектор 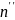можно заме­нить на 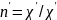, но в силу поперечности электромагнитного поля 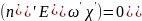. В результате, с учетом (2), имеем

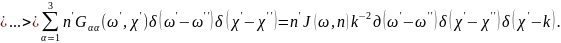
Подставляя это выражение в (3), получаем

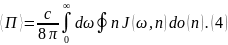
Из (4) следует, что величина 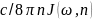имеет смысл потока энергии через единичную площадку в единичный телесный угол в расчете на единич­ный частотный интервал. Именно так вводится лучевая интенсивность (яркость) в феноменологической теории переноса излучения.

Тема 3. Метод безграничного хаотического экрана.

План проведения занятий по теме:

• Закрепление теоретических навыков по теме «Постановка задач статистической теории распространения волн»;

• Отработка практических навыков расчёта параметров поля за хаотическим безграничном экраном;

• Развитие памяти и творческого мышления;

• Контроль знаний, умений и навыков студентов, который проводится в ходе занятия при оценке ответов у доски и во время устного опроса;

• По итогам занятия производится выдача задания для самостоятельной работы.

Вопросы и задания

Задача 1. Пусть поле в плоскости экрана вещественно и распределено по нор­мальному закону. Показать, что квадрат индекса мерцаний в дальней зоне вдвое меньше, чем на экране.

Решение. В дальней зоне, согласно (3.38), 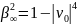. На экране же

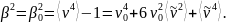
Но для вещественного нормального случайного поля 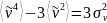. Поэтому, с учетом нормировки , имеем

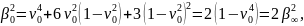
т. е. 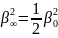. В этой н предыдущей задачах 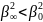, потому что поле v порождает за экраном помимо амплитудных еще и фазовые флуктуации, кото­рые, очевидно, не влияют на величину флуктуации интенсивности.

Задача 2. Вывести из френелеьскосо приближении (2.17) соотношение (3.13). согласно которому при падении плоской волны корреляционная функция за бесконечным экраном 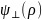совпадает с функцией корреляции граничного поля

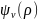
Решение. Во френелевском приближении

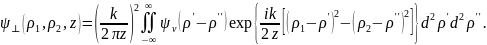
Вводя обозначения 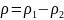, , 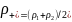, 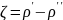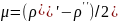. получаем выражение

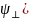
Интеграл по 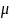здесь вычисляется точно и равен 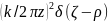. что и при­водит к соотношению = .
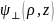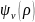