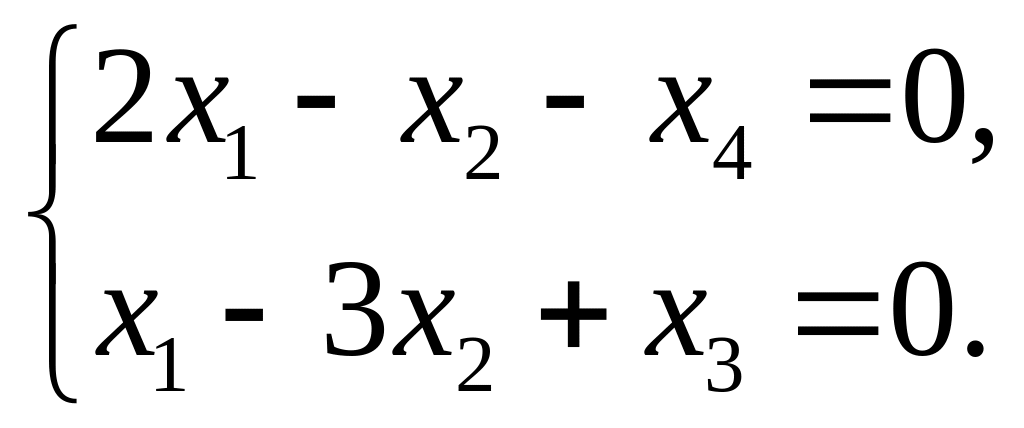- •Тема №1. Линейные пространства Теоретические вопросы темы
- •Линейные пространства
- •Линейная зависимость систем векторов
- •Базис и размерность линейного пространства решений однородной системы линейных алгебраических уравнений (ослау)
- •Формулы перехода от базиса к базису. Формулы преобразования координат при переходе от базиса к базису
- •Подпространства линейных пространств. Сумма и пересечение подпространств
- •Скалярное произведение векторов, евклидовы пространства
- •Процесс ортогонализации Шмидта
- •Дополнение системы векторов до ортогонального базиса
- •Тема №2. Линейные операторы Теоретические вопросы темы
- •Линейные операторы, их структуры
- •Структура линейного оператора
- •Матрицы линейного оператора в разных базисах
- •Собственные числа и собственные векторы линейного оператора
- •Сопряженные линейные операторы
- •Теорема Фредгольма, ее применение к исследованию слау
- •Ортогональные матрицы и ортогональные операторы
- •Приведение матрицы линейного оператора к диагональному виду
- •Тема №3. Квадратичные формы Теоретические вопросы темы
- •Квадратичные формы, их канонический вид. Метод Лагранжа приведения квадратичной формы к каноническому виду
- •Метод ортогональных преобразований приведения квадратичной формы к каноническому виду. Знакоопределенные и знакопеременные квадратичные формы
- •Библиографический список
Дополнение системы векторов до ортогонального базиса
Пусть в евклидовом пространстве :
![]() ,
,
![]() (1.7)
(1.7)
есть ортогональная система векторов: , , .
Систему векторов (1.7) можно дополнить до ортогонального базиса
![]() .
.
Вектор
![]() подбирается так, чтобы он был ортогонален
векторам
.
При этом необходимо решить систему
подбирается так, чтобы он был ортогонален
векторам
.
При этом необходимо решить систему
![]() ,
,
![]() ,
…,
,
…,
![]() ,
(1.8)
,
(1.8)
содержащую
![]() -уравнений
(
)
с
-неизвестными
-уравнений
(
)
с
-неизвестными
![]() .
Из общего решения этой системы необходимо
выделить нетривиальное частное решение,
которое определит координаты вектора
.
Из общего решения этой системы необходимо
выделить нетривиальное частное решение,
которое определит координаты вектора
![]() .
.
Вектор
![]() подбирается так, чтобы он был ортогонален
векторам
подбирается так, чтобы он был ортогонален
векторам
![]() .
При этом необходимо решить систему
.
При этом необходимо решить систему
![]() ,
,
![]() ,
…,
,
…,
![]() ,
,
![]() .
(1.9)
.
(1.9)
Система
(1.9) будет содержать (
+1)-уравнение
(если
![]() )
с
-неизвестными
)
с
-неизвестными
![]() .
Из общего решения этой системы необходимо
выделить нетривиальное частное решение,
определяющее координаты вектора
.
Из общего решения этой системы необходимо
выделить нетривиальное частное решение,
определяющее координаты вектора
![]() .
И так далее. В итоге получим систему
ортогональных векторов
.
И так далее. В итоге получим систему
ортогональных векторов
,
являющуюся ортогональным базисом в пространстве .
Задание 9.
Проверить ортогональность векторов
,
пространства
![]() и дополнить эти векторы до ортогонального
базиса.
и дополнить эти векторы до ортогонального
базиса.
9.1.
![]()
9.2.
![]()
9.3.
![]()
9.4.
![]()
9.5.
![]()
9.6.
![]()
9.7.
![]()
9.8.
![]()
9.9.
![]()
9.10.
![]()
9.11.
![]()
9.12.
![]()
9.13.
![]()
9.14.
![]()
9.15.
![]()
9.16.
![]()
9.17.
![]()
9.18.
![]()
9.19.
![]()
9.20.
![]()
Задание 10.
Подпространство
![]() линейного пространства
задано однородной системой линейных
алгебраических уравнений (ОСЛАУ). Найти
ортогональную проекцию
линейного пространства
задано однородной системой линейных
алгебраических уравнений (ОСЛАУ). Найти
ортогональную проекцию
![]() вектора
вектора
![]() на подпространство
и его ортогональную составляющую
на подпространство
и его ортогональную составляющую
![]() .
.
Алгоритм решения задания следующий.
1. Находим общее
решение ОСЛАУ и фундаментальную систему
решений
![]() (базис пространства решений ОСЛАУ).
(базис пространства решений ОСЛАУ).
2. Проверяем
ортогональность векторов
.
Если векторы не ортогональны, то проводим
процесс ортогонализации Шмидта, получаем
систему ортонормированных векторов
![]() :
:

3. Ортогональную проекцию – вектор составляем по правилу
![]() ,
,
где
![]() ,
,
![]() ,
….,
,
….,
![]() .
Проверяем принадлежность составленного
вектора
.
Проверяем принадлежность составленного
вектора
![]() пространству
.
пространству
.
4. Ортогональную составляющую – вектор составляем как
![]() .
.
Ортогональность
векторов
,
проверяем условием
![]() .
.
10.1.
|
10.2.
|
10.3.
|
10.4.
|
10.5.
|
10.6.
|
10.7.
|
10.8.
|
10.9.
|
10.10.
|
10.11.
|
10.12.
|
10.13.
|
10.14.
|
10.15.
|
10.16.
|
10.17.
|
10.18.
|
10.19.
|
10.20.
|
Задание 11.
Найти базис
![]() ортогонального дополнения линейного
подпространства
ортогонального дополнения линейного
подпространства
![]() для соответствующего линейного
подпространства
решений ОСЛАУ задания 3. Написать ОСЛАУ,
соответствующую подпространству
.
для соответствующего линейного
подпространства
решений ОСЛАУ задания 3. Написать ОСЛАУ,
соответствующую подпространству
.