Подпространства линейных пространств. Сумма и пересечение подпространств

Непустое подмножество векторов линейного пространства называется подпространством, если для любых векторов и любых чисел вектор .

Суммой двух подпространств называется множество векторов , которые можно представить в виде

.

Пересечением двух подпространств называется множество векторов , которые принадлежат одновременно обоим подпространствам: .

Задание 6. Найти базисы и размерности линейных подпространств

, , если , .

6.1.
6.2.
6.3.
6.4.
6.5.
6.6.
6.7.
6.8.
6.9.
6.10.
6.11.
6.12.
6.13.
6.14.
6.15.
6.16.
6.17.
6.18.
6.19.
6.20.

Скалярное произведение векторов, евклидовы пространства

Если в линейном пространстве любым двум векторам можно поставить в соответствие действительное число , называемое скалярным произведением и удовлетворяющее условиям (аксиомам):

1) , 2) , ,

3) ,

4) , причем тогда и только тогда, когда ,

то это пространство называется евклидовым пространством.

Число называется нормой вектора . При этом для любых векторов справедливо неравенство Коши-Буняковского

.

Задание 7. Проверить, задает ли операция ( – элементы матрицы ), определенная для векторов , пространства , скалярное произведение.

7.1.	7.2.	7.3.
7.4.	7.5.	7.6.
7.7.	7.8.	7.9.
7.10.	7.11.	7.12.
7.13.	7.14.	7.15.
7.16.	7.17.	7.18.
7.19.	7.20.

Процесс ортогонализации Шмидта

Система векторов евклидова пространства со скалярным произведением ( ) называется ортогональной, если эти векторы взаимно ортогональны [ при всех , ]. Ортогональная система векторов линейно независима.

В евклидовом пространстве размерности существует ортонормированный базис . Этот базис можно построить по линейно независимой системе векторов с помощью процесса ортогонализации Шмидта:

;	, ;
;	, , ;
;	, , , ;
………………………………………	…………………………..
	, , , , … .

Задание 8. Доказать, что система векторов , , пространства является базисом. Построить по этой системе ортонормированный базис (провести процесс ортогонализации Шмидта).

8.1.	.
8.2.	.
8.3.	.
8.4.	.
8.5.	.
8.6.	.
8.7.	.
8.8.	.
8.9.	.
8.10.	.
8.11.	.
8.12.	.
8.13.	.
8.14.	.
8.15.	.
8.16.	.
8.17.	.
8.18.	.
8.19.	.
8.20.	.
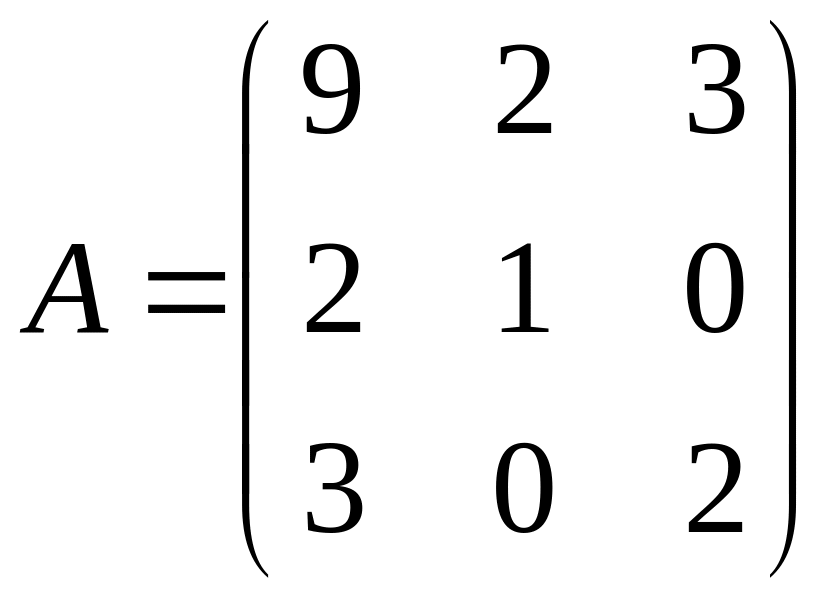
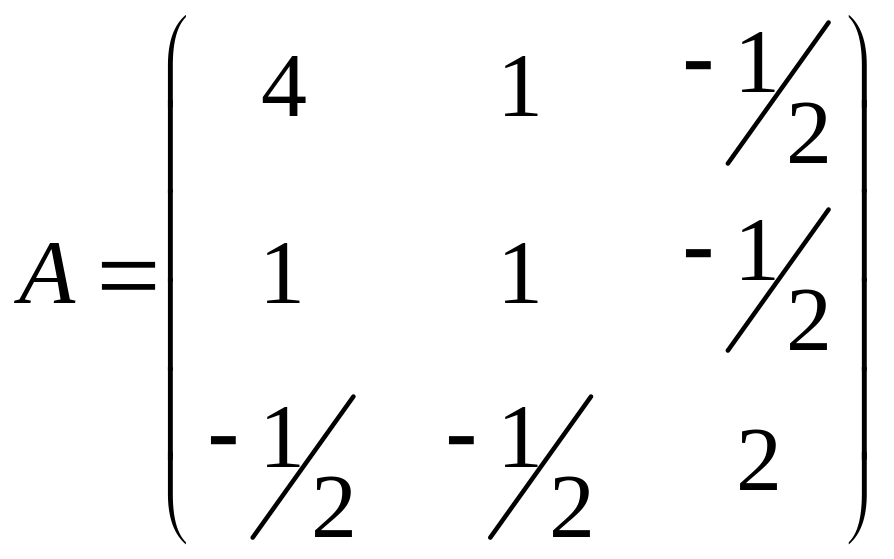
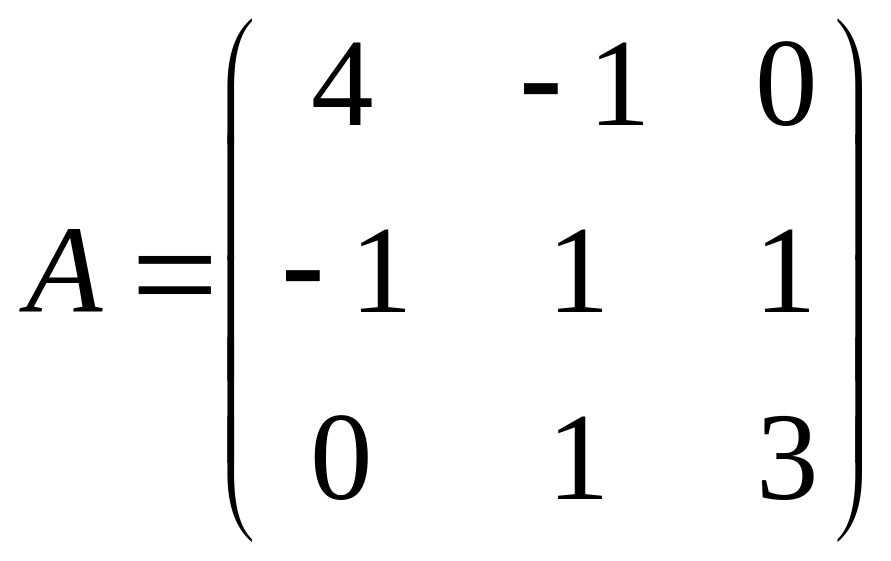