Тема 6. «Аналіз концентрації, диференціації та подібності розподілів»

Задача 1.

Розподіл підприємства і чисельності працюючих за видами економічної діяльності в одному з регіонів характеризується даними:

Галузі економічної діяльності	Кількість підприємств	Структура підприємств, dj%	Чисельність працюючих, тис. осіб	Структура працюючих, Dj%
Добувні	1400	21,4	180,9	33,3
Обробні	3545	54,2	313,6	57,8
Будівництва	1600	24,4	48,2	8,9
Разом	6545	100	542,7	100

Розрахуйте коефіцієнти локалізації та концентрації чисельності працюючих у регіоні. Зробіть висновки.

Рішення.

1. Знайдемо структуру підприємства (d_j) та працюючих (D_j), %:

а) у добувній галузі:

d_jд = 1400/6545*100% = 21,4%

D_jд = 180,9/542,7*100% = 33,3%;

б) в обробній:

d_jо = 3545/6545*100% = 54,2%

D_jо = 313,6/542,7*100% = 57,8%;

в) у будівничій:

d_jб = 1600/6545*100% = 24,4%

D_jб = 48,2/542,7*100% = 8,9%.

2. Знайдемо коефіцієнт локалізації чисельності працюючих у регіоні(L_j):

а) добувної галузі:

L_jд = D_jд/d_jд = 33,3/21,4 = 1,56;

б) обробної:

L_jо = D_jо/d_jо = 57,8/54,2 = 1,07;

в) будівничої:

L_jб = D_jб/d_jб = 8,9/24,4 = 0,36.

3. Знайдемо коефіцієнт концентрації чисельності працюючих у регіоні(К):

К = d_jо-D_jо = = = 15,5

Задача 2.

На наступний звітний рік структура підприємств регіону, яка наведена у попередній задачі змінилася наступним чином:

Галузі економічної діяльності	Кількість підприємств	Структура підприємств, dj%
Добувні	3546	21,3
Обробні	4657	27,9
Будівництва	8467	50,8
Разом	16670	100

Рішення.

1. Знайдемо зміну в структурі підприємств (d_і), %:

а) в добувній галузі:

d_ід = 3546/16670*100% = 21,3%;

б) в обробній:

d_іо = 4657/16670*100% = 27,9%

в) у будівничій:

d_іб = 8467/16670*100% = 50,8%.

2. Знайдемо лінійне відхилення часток (l_d):

l_d = = = = 17,6

3. Знайдемо квадратичне відхилення часток (_d):

_d = = = = = 21,52

Тема 7. «Статистичні методи вимірювання взаємозв’язків»

Задача 1.

По групі сімей відомі дані про дходи та витрати на розваги (на одного члена сім’ї):

Доходи за місяць, грн	5400	6300	7400	9000	11200	14000	19000
Витрати на розваги, грн	800	1000	1100	1300	1500	1700	1900

Розрахуйте параметри рівняння кореляційної залежності між доходами сімей і витратами на розваги та проаналізуйте їх значення. Перевірте істотності зв’язку з імовірністю 0,95.

Рішення.

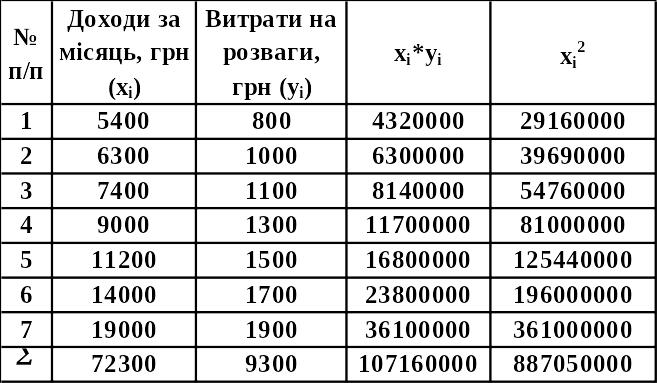
1. Розрахуємо параметри за допомогою рівняння (Y):

Y = a+bx

а) Параметри b дорівнюватимуть:

b = = = = 0,079

б) параметр а

Для розрахунку параметра «а» необхідно визначити середнє значення факторної та результативної ознаки по формулі середньої арифметичної простої: = 72300/7 = 10328,57; = 9300/7 = 1328,57.

а = 1328,57-0,079*10328,57 = 512,61 грн

отже:

Y = 512,6+0,079х

Це означає, що з зростанням доходу на 1 грн , витрати на розваги збільшаться на 0,079 грн. При відсутності росту доходу обсяг витрат на розваги складатиме 512,6 грн.

Задача 2.

В результаті обстеження затримки літаків в аеропорті із-за певних метеорологічних умов отримані наступні дані, які зведені до таблиці:

Метеорологічні умови	Кількість вилетів	Середній час затримки літака, годин
Несприятливі	25	8
Нестійкі	35	4
Сприятливі	40	1
Разом	100	3,8

Визначте між групову, середню з групових дисперсій часу затримки вилетів, якщо відомо, що загальна дисперсія дорівнює 10. Визначте як впливають метеорологічні умови на середній час затримки літаків. Перевірте істотність зв’язку з імовірністю 0,95.

Рішення.

1. Знайдемо міжгрупову дисперсію (²):

² =

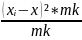
де: х_і - середній час затримки літака(годин), де і - метеорологічні умови;

х_с - загальний середній час затримки літака, годин

х_с = 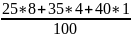= 3,8;

m_i­ - кількість вилетів.

² = = = 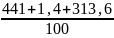7,56

2. Знайдемо середню з групових дисперсій (_с²):

_с² = ² - ² = 10 -7,56 = 2,44